Примеры решения задач с векторами

Примеры решения задач с векторами

Вектора применяются во многих науках, таких как: математика, физика, геометрия и многих других прикладных науках. На практике, они позволяют не делать лишних операций и сократить время выполнения задач. Поэтому, будущим специалистам очень важно понять теорию векторов и научиться решать задачи с ними.

Перед изучением примеров решения задач советуем изучить теоретический материал по векторам, прочитать все определения и свойства. Список тем находится в правом меню.

Координаты вектора

Теоретический материал по теме - координаты вектора.

Пример

Запись означает, что вектор имеет следующие координаты: абсцисса равна 5, ордината равна -2.

Пример

Задание. Заданы векторы и . Найти координаты вектора

Решение.

Пример

Задание. Вектор . Найти координаты вектора

Решение.

Пример

Задание. Найти координаты вектора , если

Решение.

Длина (модуль) вектора

Теоретический материал по теме - длина вектора.

Пример

Задание. Найти длину вектора

Решение. Используя формулу, получаем:

Пример

Задание. Найти длину вектора

Решение. Используя формулу, получаем:

Угол между векторами

Теоретический материал по теме - угол между векторами.

Пример

Задание. Известно, что скалярное произведение двух векторов , а их длины . Найти угол между векторами и .

Решение. Косинус искомого угла:

Пример

Задание. Найти угол между векторами и

Решение. Косинус искомого угла

Пример

Задание. Найти угол между векторами и

Решение. Косинус искомого угла:

Разложение вектора по ортам координатных осей

Теоретический материал по теме - разложение вектора по ортам.

Пример

Задание. Зная разложения вектора по базисной системе векторов: , записать координаты этого вектора в пространстве.

Решение. Коэффициенты при ортах и есть координатами вектора, поэтому из того, что , получаем, что

Пример

Задание. Вектор задан своими координатами: . Записать разложение данного вектора по ортам осей координат.

Решение. Координаты вектора - это коэффициенты при ортах координатных осей в разложении вектора по базисной системе векторов, поэтому искомое разложение:

Скалярное произведение векторов

Теоретический материал по теме - скалярное произведение векторов.

Пример

Задание. Вычислить скалярное произведение векторов и , если их длины соответственно равны 2 и 3, а угол между ними 60°.

Решение. Так как из условия , , а , то

Пример

Задание. Найти скалярное произведение векторов и

Решение. Скалярное произведение

Векторное произведение векторов

Теоретический материал по теме - векторное произведение векторов.

Пример

Задание. Найти векторное произведение векторов и

Решение. Составляем определитель и вычисляем его:

Смешанное произведение векторов

Теоретический материал по теме - смешанное произведение векторов.

Пример

Задание. Вычислить объем пирамиды, построенной на векторах , ,

Решение. Найдем смешанное произведение заданных векторов, для это составим определитель, по строкам которого запишем координаты векторов , и :
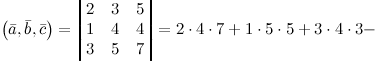