
- •Тема производная
- •§1. Задачи, приводящие к понятию производной
- •I Задача о касательной
- •II Задача о скорости
- •§2. Определение и смысл производной
- •§3. Бесконечные и односторонние производные
- •I Бесконечные производные
- •§4. Дифференцируемость функции
- •§5. Основные правила дифференцирования
- •§6. Производные основных элементарных функций
- •III Логарифмическая функция
- •IV Тригонометрические функции
- •V Обратные тригонометрические функции
- •VI Гиперболические и обратные гиперболические функции
- •VII Сводка формул для производных
- •§5 (Продолжение). Основные правила дифференцирования
- •VII Логарифмическая производная
- •VIII Дифференцирование обратной функции
- •IX Дифференцирование функции, заданной параметрически
- •X Дифференцирование функции, заданной неявно
- •§7. Дифференциал функции
- •I Определение и геометрический смысл
- •II Инвариантность формы первого дифференциала
- •III Таблица дифференциалов
- •§8. Производные высших порядков
- •I Определение и обозначения
- •II Производные некоторых функций
- •§2. Теорема о среднем значении
- •§3. Обобщение формулы конечных приращений
- •§4. Раскрытие неопределенностей. Правило Бернулли-Лопиталя
- •I Понятие неопределенного выражения
- •II Неопределенности вида ,.
- •III Другие виды неопределенностей.
III Таблица дифференциалов
Так как дифференциал dyлишь множителемdxотличается от производной![]() ,
то по таблице производных легко составить
таблицу дифференциалов.
,
то по таблице производных легко составить
таблицу дифференциалов.
1.
![]() ,
,![]() ,
,![]() .
.
2.
![]() ,
,![]() .
.
3.
![]() ,
,![]() .
.
4.
![]() . 5.
. 5.![]() .
.
6.
![]() . 7.
. 7.![]() .
.
8.
![]() . 9.
. 9.![]() .
.
10.
![]() . 11.
. 11.![]() .
.
Также легко получить формулы для дифференциалов суммы, разности, произведения и частного функций:
а)
![]()
б)
![]()
в)
![]()
Отметим, что в таблице дифференциалов переменная xможет быть как независимой, так и некоторой функцией. В таблице же производных (§6)x– это только независимая переменная.
Замечание.Формула для дифференциала
функции![]() ,
а именно:
,
а именно:
![]() ,
,
позволяет написать формулу, выражающую производную функции через дифференциалы dxиdy:
![]() .
.
При этом такая формула сохраняет силу, по какой бы независимой переменной ни были вычислены dxиdy. Эта формула позволяет легко запоминать (но не доказывать!) некоторые правила дифференцирования:
для сложной функции
![]()
![]() ;
;
для обратной функции
 ;
;
для функции, заданной параметрически
![]()
![]() .
.
§8. Производные высших порядков
I Определение и обозначения
Если функция
![]() дифференцируема на некотором промежутке,
то её производная
дифференцируема на некотором промежутке,
то её производная![]() сама является функцией, определенной
на этом промежутке. Следовательно, по
отношению к ней можно ставить вопрос о
существовании и нахождении производной.
Если она существует, то её называют
второй производной (или производной
2гопорядка), и обозначают одним
из символов
сама является функцией, определенной
на этом промежутке. Следовательно, по
отношению к ней можно ставить вопрос о
существовании и нахождении производной.
Если она существует, то её называют
второй производной (или производной
2гопорядка), и обозначают одним
из символов
![]() .
.
Аналогично, если существует производная
от второй производной, то её называют
третьей производной и обозначают,
например,
![]() .
.
Вообще, производной n-го
порядка называют производную от
производной (n–1)-го
порядка и обозначают![]() .
Итак, по определению
.
Итак, по определению
![]() .
.
II Производные некоторых функций
1. y=sinx, y=cosx
Первые производные этих функций
![]() и формулы приведения
и формулы приведения![]() позволяют методом математической
индукции получить выражения для
производныхn-го
порядка:
позволяют методом математической
индукции получить выражения для
производныхn-го
порядка:
![]() .
.
2. y=x
Если
![]() ,
то, последовательно дифференцируя,
получим
,
то, последовательно дифференцируя,
получим![]() ,
,![]() ,
и вообще:
,
и вообще:
![]() .
.
Если же показатель степени натуральный, то:

3. y=ax
![]() ,
в частности,
,
в частности,![]() ,
,![]() .
.
4. y=lnx
![]() ,
,
![]() .
.
III Некоторые правила
Очевидно, что
![]() и
и![]() .
Для производной
.
Для производной
n-го порядка от произведения функций имеется т.н. формула Лейбница. Приведем ее без доказательства:
![]() ,
где
,
где![]() .
.
Заметим, что под производной нулевого порядка принято понимать саму
функцию:
![]() .
.
IV Функция, заданная параметрически
Пусть функция задана параметрическими уравнениями
![]()
Её первая производная – это также функция, заданная параметрически:
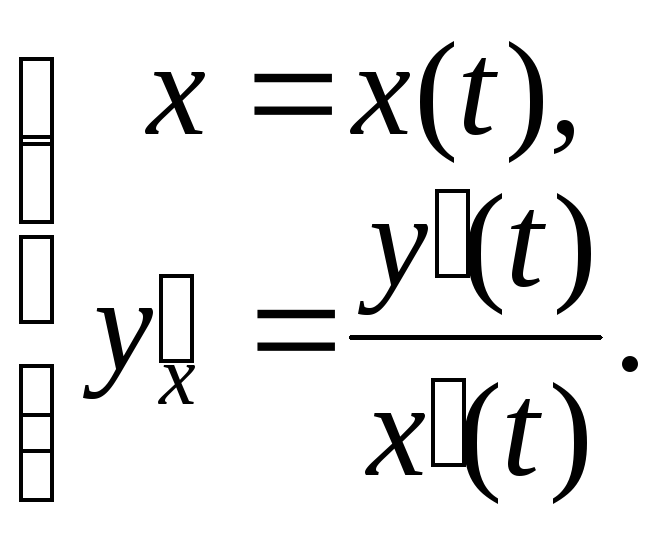
Тогда
![]()
Пример.Для![]() первая производная имеет вид
первая производная имеет вид![]() Тогда
Тогда![]() и вторая производная такова:
и вторая производная такова:![]()
V Функция, заданная неявно
Повторное дифференцирование такой функции покажем на примере:
![]()
Тогда по определению:
![]() .
.
Остается подставить в последнее выражение
значение
![]() :
:
 .
.
Полученное выражение можно упростить, используя само уравнение:
![]() .
.
Тема ОСНОВНЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ
Лекция 10
§1. Необходимое условие экстремума
Рассмотрим функцию
![]() ,
определенную на промежутке
,
определенную на промежутке![]() ,
и пусть точка
,
и пусть точка![]() –внутренняяточка промежутка:
–внутренняяточка промежутка:![]() .
.
Определение 1.Точка![]() называется точкой (локального) максимума
функции
называется точкой (локального) максимума
функции![]() ,
если существует окрестность этой точки,
в которой (при
,
если существует окрестность этой точки,
в которой (при![]() )
выполняется неравенство
)
выполняется неравенство![]() .
Другими словами для малых приращений
аргумента
.
Другими словами для малых приращений
аргумента![]() приращение
функции
приращение
функции![]() .
.
Определение 2.Точка![]() называется точкой (локального) минимума
функции
называется точкой (локального) минимума
функции![]() ,
если существует окрестность этой точки,
в которой (при
,
если существует окрестность этой точки,
в которой (при![]() )
выполняется неравенство
)
выполняется неравенство![]() .
Другими словами
.
Другими словами![]() при малых
при малых![]() .
.
Точки максимума и минимума называются
точками экстремума. Их можно характеризовать
следующим образом: приращение функции
в точке экстремума имеет постоянный
знак, не зависящий от знака
![]() (если
(если![]() достаточно мало).
достаточно мало).
Теорема Ферма.Если функция![]() дифференцируема в точке
дифференцируема в точке![]() и имеет в этой точке локальный экстремум,
то
и имеет в этой точке локальный экстремум,
то![]() .
.
Доказательство.Дифференцируемость означает существование конечного предела
![]() .
.
Для этого предела имеется три возможности:
1)
![]() ;
2)
;
2)![]() ;
;
3)
![]() .
Предположим, что
.
Предположим, что![]() .
Тогда для близких к нулю
.
Тогда для близких к нулю![]() разностное отношение
разностное отношение![]() .
Если же
.
Если же![]() ,
то и
,
то и![]() (для малых
(для малых![]() ).
В обоих случаях знак
).
В обоих случаях знак![]() зависит от знака
зависит от знака![]() .
Но по условию теоремы
.
Но по условию теоремы![]() – это точка экстремума, значит, знак
– это точка экстремума, значит, знак![]() не зависит от знака
не зависит от знака![]() .
Это противоречие означает, что
.
Это противоречие означает, что![]() не может быть ни положительным, ни
отрицательным. Остается последняя
возможность:
не может быть ни положительным, ни
отрицательным. Остается последняя
возможность:![]() .
.
Замечание 1.Эта теорема имеет
простой геометрический смысл: если в
точке графика функции![]() ,
которой соответствует экстремум функции,
существует касательная к графику, то
эта касательная параллельная осиOx.
,
которой соответствует экстремум функции,
существует касательная к графику, то
эта касательная параллельная осиOx.
Замечание 2.Сформулированное
в теореме условие![]() является необходимым, но не достаточным.
Например, функция
является необходимым, но не достаточным.
Например, функция![]() имеет производную
имеет производную![]() ,
которая обращается в ноль в точке
,
которая обращается в ноль в точке![]() .
Однако,
.
Однако,
![]() .
.
Выражение в скобках всегда положительно,
как неполный квадрат суммы. Следовательно,
![]() и в точке
и в точке![]() нет экстремума.
нет экстремума.
