электроприводов, объединенных сложной системой управ­ления, обеспечивающей интенсифицированный режим ра­боты, логическую бесперебойную последовательность управ­ления многочисленными механическими, гидравлическими и электрическими устройствами.

Комплексная автоматизация других объектов, напри­мер поточно-транспортных систем, доменного и прокат­ного производства, бумагоделательных агрегатов и т. д. на базе широкого применения автоматизированного элек­тропривода с использованием УВМ, способствует повыше­нию производительности труда, улучшению качества про­дукции.

Развитие автоматического управления электроприво­дами ведет к совершенствованию конструкций машин, коренным изменениям технологического процесса, к даль­нейшему техническому прогрессу в промышленности, сель­ском хозяйстве, транспорте и т. п.

ГЛАВА ВТОРАЯ

МЕХАНИКА ЭЛЕКТРОПРИВОДА

2.1. Приведение моментов и сип

сопротивления, инерционных масс и моментов инерции

Обычно двигатель приводит в действие производственный механизм через систему передач, отдель­ные элементы которой движутся с различными скоростями. Примерная кинематическая схема электропривода с вра­щательным движением исполнительного механизма пред­ставлена на рис. 2.1.

Часто в рабочих механизмах один из элементов совер­шает вращательное движение, другие — поступательное, например в таких машинах, как подъемник (рис. 2.2), кран, строгальный станок и т. п.

Механическая часть электропривода может представ­лять собой сложную кинематическую цепь с большим числом движущихся элементов. Каждый из элементов реальной кинематической цепи обладает упругостью, т. е. деформируется под нагрузкой, а в соединениях элементов имеются воздушные зазоры. Если учитывать эти факторы, то расчетная схема механической части привода будет

представлена многомассовой механической системой с упру­гими связями и зазорами, расчет динамики которой состав­ляет большие трудности и возможен только посредством ЭВМ. Однако основные закономерности движения таких систем определяются наибольшими массами и зазорами и наименьшими жесткостями связей системы, что позво­ляет свести расчетную схему механической части привода либо к трехмассовой, либо к двухмассовой механической системе с эквивалентными упругими связями и с суммар­ным зазором (или без него), приведенным к угловой ско­рости вала двигателя. Но и эти расчетные схемы исполь­зуются в тех ответственных случаях, где пренебрежение

Механизм

Рис. 2.1. Кинематическая схема связи двигателя с исполнитель­ным механизмом.

Рис. 2.2. Кинематическая схема привода подъемника.

упругостью и зазором приведет к большим ошибкам рас­чета (точные следящие системы радиотелескопов и метал­лорежущих станков; механизмы с гибкими связями, длин­ными валами, канатами; резкие изменения состояния системы и т. п.). Методика расчета электроприводов, меха­ническая часть которых содержит упругие связи и зазоры, рассмотрена в [42].

В большинстве практических случаев в инженерных расчетах при решении задач, не требующих большой точ­ности, и для механических звеньев, обладающих неболь­шими зазорами и незначительной упругостью (большой жесткостью), можно пренебречь зазорами и упругостью, приняв механические связи абсолютно жесткими. При этом допущении движение одного элемента дает полную информацию о движении всех остальных элементов, по­этому движение электропривода можно рассматривать на каком-либо одном механическом элементе. Обычно в качестве такого элемента принимают вал двигателя.

Расчетную схему механической части привода, следова­тельно, можно свести к одному обобщенному жесткому механическому звену, имеющему эквивалентную массу с моментом инерции J, на которую воздействует электро­магнитный момент двигателя М и суммарный приведенный к валу двигателя момент сопротивления (статический мо­мент) М_С, включающий все механические потери в си­стеме, в том числе механические потери в двигателе.

Момент сопротивления механизма М_С,М (рис. 2.1), возникающий на валу рабочей машины, состоит из двух слагаемых, соответствующих полезной работе и работе трения.

П о л е з н а я работа, совершаемая производст­венным механизмом, связана с выполнением соответствую-

щей технологической операции. График полезной работы может быть построен на основании ана­литических расчетов или по экс­периментальным данным. Такой график, например, для станка,

Рис. 2.3. Циклический график работы станка.

работающего по циклическому закону, представлен на рис. 2.3. Заштрихованная область графика соответствует полезной работе; незаштрихованная часть графика соот­ветствует работе трения. При совершении полезной ра­боты происходит деформация материала или изменяется запас потенциальной энергии тел, например в подъем­ных устройствах. В некоторых машинах совершение по­лезной работы связано с незначительным превышением момента по сравнению с моментом трения (например, печатная машина, размольная шаровая мельница, кран, передвигающийся по горизонтальным направляющим, и т. п.).

Работа трения, совершаемая в производствен­ном механизме, учитывается обычно КПД механических связей привода. Работу трения можно иногда учесть, пользуясь данными, полученными на основании опыта. Например, при подъеме груза G1 на высоту h можно счи­тать, что силы трения как бы увеличивают вес груза на некоторое дополнительное значение G₀. Тогда работа подъ-

ема, Дж, записывается следующим образом:

A=h(G₁ + G₀). (2.1)

В насосах потери могут учитываться некоторой фиктив­ной дополнительной высотой подачи h₀. Момент трения всегда направлен против движущего момента привода.

Моменты сопротивления можно разделить на две кате­гории, а именно: 1) реактивные моменты и 2) активные или потенциальные мо­менты.

В первую категорию включаются моменты сопротивления от сжатия, резания, моменты трения и т. п., препятствую­щие движению привода и изменяющие свой знак при изме­нении направления вращения.

Во вторую категорию входят моменты от силы тяжести, а также от растяжения, сжатия и скручивания упругих тел. Эти моменты могут быть названы потенциальными, поскольку они связаны с изменением потенциальной энер­гии отдельных элементов привода. Потенциальные моменты могут тормозить движение привода или, наоборот, способ­ствовать его движению. Следует отметить, что в отличие от реактивного статического момента активный момент сохраняет свой знак при изменении направления вращения привода. Например, момент, создаваемый грузом подъем­ного механизма, сохраняет свой знак как при подъеме сто, так и при опускании. Следовательно, в данном случае активный статический момент при подъеме препятствует движению, а при опускании способствует ему.

Приведение моментов сопротивления от одной оси вра­щения к другой может быть произведено на основании энергетического баланса системы. При этом потери мощ­ности в промежуточных передачах учитываются введением в расчеты соответствующего КПД — η_п. Обозначим через ω_д угловую скорость вала двигателя, а ω_м — угловую ско­рость вала производственного механизма. На основании равенства мощностей получим:

откуда

(2.2)

где M_C,M — момент сопротивления производственного ме­ханизма, Н·м; M_С ­– тот же момент сопротивления, при-

веденный к скорости вала двигателя, Н·м;

передаточное число.

При наличии нескольких передач между двигателеми механизмом (см. рис. 2.1) с передаточными числами и соответствующими КПД мо-

мент сопротивления, приведенный к скорости вала двига­теля, определяется формулой

(2.3)

Приведение сил сопротивления производится анало­гично приведению моментов. Если скорость поступатель­ного движения v, м/с, а угловая скорость вала двига­теля ω_Д , рад/с, то

(2.4)

где F_C,M — сила сопротивления производственного меха­низма, Н.

Отсюда приведенный к скорости вала двигателя момент сопротивления равен:

(2.5)

В случае приведения вращательного движения к посту­пательному приведенное усилие

(2.6)

Приведение моментов инерции к одной оси вращения основано на том, что суммарный запас кинетической энер­гии движущихся частей привода, отнесенный к одной оси, остается неизменным. При наличии вращающихся частей, обладающих моментами инерции J_Д, J₁, J₂, …,J_n и угло­выми скоростями ω_Д, ω₁, ω₂, …,ω_n (см. рис. 2.1), можно заменить их динамическое действие действием одного момента инерции, приведенного например, к скорости вала двигателя. В таком случае можно написать:

(2.7)

откуда результирующий или суммарный момент инерции, приведенный к валу двигателя:

(2.8)

где J_д — момент инерции ротора двигателя и других элементов (муфты, шестерни и т. п.), установленных на валу двигателя.

Иногда в каталогах для двигателей указывается зна­чение махового момента GD², кгс ·м². В этом случае моменты инерции ротора двигателя, кг ·м², в си­стеме СИ вычисляются по формуле

J_p = GD²/4, (2.9)

где D — диаметр инерции, м; G — сила тяжести (вес), кгс. Это соотношение следует из формулы, определяющей момент инерции тела массой m, кг,

J = mρ², (2.10)

где ρ — радиус инерции, м.

Если сила тяжести выражена в ньютонах, то масса тела определяется из равенства

G = mg, (2.11)

где g = 9,81 м/с² — ускорение свободного падения.

Момент инерции сплошного цилиндра относительно продольной оси вычисляется по формуле

J = mR²/2, (2.12)

где R — радиус цилиндра, м.

Приведение масс, движущихся поступательно, осуще­ствляется также на основании равенства запаса кинети­ческой энергии

Отсюда момент инерции, приведенный к валу двигателя, J = m(v/ω_Д)². (2.13)

Если механизм имеет вращающиеся и поступательно движущиеся элементы, то суммарный приведенный к валу двигателя момент инерции определяется на основании (2.8) и (2.13)

(2.14)

Для приведения момента инерции к поступательному движению нужно момент инерции заменить приведенной массой, т. е.

m = J (ω_Д /v)². (2.15)

2.2. Механические характеристики производственных механизмов и электрических двигателей. Установившиеся режимы

При рассмотрении работы электродвига­теля, приводящего в действие производственный меха­низм, необходимо прежде всего выявить соответствие механических характеристик двигателя характеристике производственного механизма. Поэтому для правильного проектирования и экономичной эксплуатации электро­привода необходимо изучить эти характеристики.

Зависимость между приведенными к валу двигателя скоростью и моментом сопротивления механизма ω = = f (М_с) называют механической характери­стикой производственного механизма.

Различные производственные механизмы обладают раз­личными механическими характеристиками. Однако можно получить некоторые обобщающие выводы, если воспользо­ваться следующей эмпирической формулой для механиче­ской характеристики производственного механизма:

(2.16)

где M_С — момент сопротивления производственного меха­низма при скорости ω; М₀ — момент сопротивления тре­ния в движущихся частях механизма; М_с,_ном — момент сопротивления при номинальной скорости ω_ном; х — пока­затель степени, характеризующий изменение момента сопро­тивления при изменении скорости.

Приведенная формула позволяет классифицировать ме­ханические характеристики производственных механизмов ориентировочно на следующие основные категории:

1. Н е зависящая от скорости меха­ническая характеристика (прямая 1 на рис. 2.4). При этом х = 0 и момент сопротивления М_с не зави­сит от скорости. Такой характеристикой обладают, напри­мер, подъемные краны, лебедки, механизмы подач метал­лорежущих станков, поршневые насосы при неизменной высоте подачи, конвейеры с постоянной массой передвигае­мого материала. Сюда же могут быть отнесены с известным приближением все механизмы, у которых основным момен­том сопротивления является момент трения, так как обычно в пределах рабочих скоростей момент трения изменяется мало.

2. Л и н е и н о - возрастающая механиче­ ская характеристика (прямая 2 на рис. 2.4). В этом случае х= 1 и момент сопротивления линейно за­ висит от скорости ω, увеличиваясь с ее возрастанием (для упрощения принято М₀ = 0).

Такая характеристика получится, например, в приводе генератора постоянного тока с независимым возбуждением, если последний будет работать на постоянный внешний резистор.

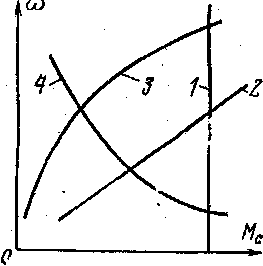
3. Нелинейно-возрастающая (парабо- лическа я) механическая характеристи- к а (кривая 3 на рис. 2.4). Этой характеристике соответст­ вует х = 2; момент сопротивления М_с здесь зависит от квадрата скорости. Механизмы, обла­ дающие такой характеристикой, назы­ вают иногда механизмами с вентиля­ торным моментом, поскольку у вен­ тиляторов момент сопротивления за­ висит от квадрата скорости. К меха-

Рис. 2.4. Механические характеристики про­изводственных механизмов.

низмам, обладающим параболической механической харак­теристикой, относятся также центробежные насосы, греб­ные винты и т. п.

4. Нелинейно-спадающая механиче­ская характеристика (кривая 4 на рис. 2.4). При этом х = –1 и момент сопротивления M_С изменяется обратно пропорционально скорости, а мощность, потреб­ляемая механизмом, остается постоянной. Такой харак­теристикой обладают, например, некоторые токарные, рас­точные, фрезерные и другие металлорежущие станки, мо­талки в металлургической промышленности и т. п. Эти характеристики не исчерпывают всех практически воз­можных случаев, но дают представление о характеристиках некоторых типичных производственных механизмов.

Механической характеристикой электродвигателя называется зависи­мость его угловой скорости от вра­щающего момента, т.е. ω = f(М). Почти все электродвигатели обладают тем свойством, что скорость их является убывающей функцией момента двигателя.

Это относится почти ко всем обычным электродвигателям, применяемым в промышленности, т. е. к двигателям постоянного тока независимого, последовательного и сме­шанного возбуждения, а также к асинхронным бесколлек­торным и коллекторным двигателям переменного тока. Однако степень изменения скорости с изменением момента у разных двигателей различна и характеризуется так называемой жесткостью их механических характеристик. Жесткость механической характе­ристики электропривода — это отношение разности электромагнитных моментов, развиваемых элек­тродвигательным устройством, к соответствующей разности угловых скоростей электропривода, т. е.

(2.17)

Обычно на рабочих участках механические характери­стики двигателей имеют отрицательную жесткость β < 0. Линейные механические характеристики обладают постоян­ной жесткостью. В случае нелинейных характеристик их жесткость не постоянна и определяется в каждой точке как производная момента по угловой скорости

(2.18)

Понятие жесткости может быть применено и к механи­ческим характеристикам производственных механизмов. Эти характеристики можно оценивать жесткостью

(2.19)

Механические характеристики электродвигателей можно разделить на четыре основные категории:

1. Абсолютно жесткая механическая характеристика (β= ∞) — это характеристика, при которой скорость с изменением момента остается неизменной. Такой характеристикой обладают синхронные двигатели (прямая 1 на рис. 2.5).

2. Жесткая механическая характери­ стика — это характеристика, при которой скорость с изменением момента хотя и уменьшается, но в малой степени. Жесткой механической характеристикой обладают двигатели постоянного тока независимого возбуждения, а также асинхронные двигатели в пределах рабочей части механической характеристики (кривая 2 на рис. 2.5).

Для асинхронного двигателя жесткость в различных точках механической характеристики различна (рис. 2.6).

Между максимальными (критическими) значениями момен­тов в двигательном M_К,_Д и генераторном М_К,Г режимах характеристика асинхронного двигателя имеет сравнительно большую жесткость.

3. Мягкая механическая характери­стика — это характеристика, при которой с изменением момента скорость значительно изменяется. Такой харак­теристикой обладают двигатели постоянного тока после­довательного возбуждения, особенно в зоне малых моментов (кривая 3 на рис. 2.5). Для этих двигателей жесткость не остается постоянной для всех точек характеристик.

Двигатели постоянного тока смешанного возбуждения могут быть отнесены ко второй или третьей группе в зави-

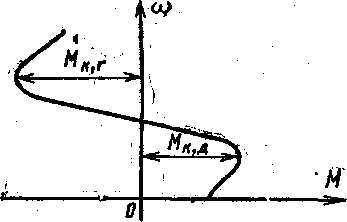
Рис. 2.5. Механические теристики двигателей.

харак-

Рис. 2.6. Механическая харак- теристика асинхронного двигателя.

симости от значения жесткости механической характери­ стики.

4. Абсолютно мягкая механическая характеристика (β = 0) — это характеристика, при которой момент двигателя с изменением угловой ско­рости остается неизменным. Такой характеристикой обла­дают, например, двигатели постоянного тока независимого возбуждения при питании их от источника тока или при работе в замкнутых системах электропривода в режиме стабилизации тока якоря (прямая 4 на рис. 2.5).

Работе электрического двигателя и производственного механизма в установившемся режиме соответствует равно­весие момента сопротивления механизма и вращающего момента двигателя при определенной скорости, т. е. М=М_С.

Изменение момента сопротивления на валу двигателя приводит к тому, что скорость двигателя и момент, который он развивает, могут автоматически изменяться и

привод будет продолжать устойчиво работать при другой скорости с новым значением момента.

Для восстановления равновесия между изменившимся моментом сопротивления и моментом двигателя во всех неэлектрических двигателях требуется участие специаль­ных регуляторов, которые воздействуют на источник энергии, увеличивая или соответственно уменьшая подачу воды, топлива или пара. В электрических двигателях роль автоматического регулятора может выполнять ЭДС двига­теля. Эта особенность электродвигателей автоматически поддерживать равновесие системы при изменяющемся мо­менте сопротивления является весьма ценным свойством, так как во многих случаях момент может изменяться в той или иной степени.

Изложенное иллюстрируется рис. 2.7, где приведены механическая характеристика 3 двигателя постоянного тока независимого возбуждения и две характеристики 1 и 2 производственного механизма, например конвейера, приводимого в движение этим двигателем ¹.

Характеристика 1 соответствует моменту сопротивле­ния М₁ при холостом ходе конвейера. Характеристика 2 получается при большом моменте сопротивления M₂ после того, как на конвейер положены транспортируемые .им детали. Вначале при холостом ходе конвейера М = М₁ двигатель работает со скоростью ω₁. С увеличением на­грузки двигатель тормозится, скорость его снижается, благодаря чему уменьшается ЭДС. При уменьшении ЭДС возрастают ток в якорной цепи двигателя и момент, раз­виваемый двигателем. Рост момента двигателя продол­жается до тех пор, пока не наступит равновесие моментов М = М₂ (точка ω₂). Эта новая точка также является общей для механической характеристики конвейера (2) и механической характеристики электродвигателя (3).

Рассмотренные условия работы электропривода в уста­новившемся режиме характеризуют статическую устойчивость привода, когда изменение во вре­мени скорости и момента происходит относительно медленно в отличие от динамической устойчивости, имеющей место при переходных режимах.

Под статической устойчивостью по­нимается такое состояние установившегося режима ра-

¹ Механические характеристики производственного механизма для удобства изображаются в первом квадранте, хотя момент сопротивле­ния имеет отрицательный знак.

боты привода, когда при случайно возникшем отклонении скорости от установившегося значения привод возвратится в точку установившегося режима. При неустойчи­вом движении любое, даже самое малое, отклонение ско­рости от установившегося значения приводит к изменению состояния привода — он не возвращается в точку устано­вившегося режима.

Привод статически устойчив, если в точке установив­шегося режима выполняется условие

или

(2.20)

(2.21)

Условие (2.20) означает, что привод статически устой­чив, если при положительном приращении угловой ско-

0 Mi М •»

I Li

Рис. 2.7. Механические харак­теристики двигателя постоян­ного тока независимого возбуж­дения и приводимого им меха­низма.

Рис. 2.8. К определению стати­ческой устойчивости привода при постоянном моменте сопро­тивления и вентиляторной на­грузке.

рости момент двигателя окажется меньше статического момента (момента сопротивления) и привод вследствие этого затормозится до прежнего значения скорости. При отрицательном приращении угловой скорости момент дви­гателя окажется больше момента сопротивления и привод вследствие этого разгонится до прежнего значения ско­рости.

При постоянном моменте нагрузки (прямая 1 на рис. 2.4) статическая устойчивость будет определяться только жест­костью механической характеристики двигателя, так как Если она отрицательна, то работа в уста-

новившемся режиме устойчива

как это имело место в рассмотренном слу­чае (рис. 2.7).

Если же использовать асинхронный двигатель с ко-роткозамкнутым ротором и нагрузить его постоянным моментом (рис. 2.8), то в точке а = —А/В — 0 < 0, т. е. устойчивый режим, а в точке б = А/C — 0 > 0, т. е. режим неустой­чивый. При работе того же двигателя на механизм с вен­тиляторной характеристикой (рис. 2.8) легко доказать, что во всех точках работа будет устойчивой.

Обычно при проектировании электропривода механиче­ская характеристика производственного механизма явля­ется уже заданной. Поэтому для получения устойчивой работы в установившемся режиме для определенных ско­ростей и моментов сопротивления производственных меха­низмов необходимо подбирать механическую характери­стику электродвигателя соответствующей формы. Это мо­жет быть достигнуто подбором электродвигателя соответ­ствующего типа и изменением электрических параметров его цепей. Иногда для получения требуемых механических характеристик приходится применять специальные схемы включения электрических машин и аппаратов.

2.1. Уравнение движения электропривода

Выше были рассмотрены условия работы электропривода в установившемся режиме, когда момент, развиваемый двигателем, равен моменту сопротивления механизма и скорость привода является постоянной. Од­нако во многих случаях привод ускоряется или замедля­ется, и тогда возникает инерционная сила или инерцион­ный момент, которые двигатель должен преодолевать, находясь в переходном режиме. Таким образом, пере­ходным режимом электропривода называют ре­жим работы при переходе от одного установившегося со­стояния к другому, когда изменяются скорость, момент и ток.

Причинами возникновения переходных режимов в элек­троприводах является либо изменение нагрузки, связан­ное с производственным процессом, либо воздействие на электропривод при управлении им, т. е. пуск, торможе­ние, изменение направления вращения и т. п. Переходные режимы в электроприводах могут возникнуть также в ре-

зультате аварий или нарушения нормальных условий электроснабжения (например, изменения напряжения или частоты сети, несимметрия напряжения и т. п.).

Уравнение движения электропривода должно учитывать все силы и моменты, действующие в переходных режимах.

При поступательном движении движущая сила F всегда уравновешивается силой сопротивления машины F_c и

инерционной силой , возникающей при изменениях

скорости. Если масса тела т выражена в килограммах, а скорость v — в метрах в секунду, то сила инерции, как и другие силы, действующие в рабочей машине, измеря­ются в ньютонах (кг∙м∙с^-2).

В соответствии с изложенным уравнение равновесия сил при поступательном движении записывается так:

F-F_с = m. (2.22)

Аналогично уравнение равновесия моментов, Н∙м, для вращательного движения (уравнение движения привода) имеет следующий вид:

(2.23)

Уравнение (2.23) показывает, что развиваемый двига­телем вращающий момент М уравновешивается моментом сопротивления М_c на его валу и инерционным или дина­мическим моментом J (2.22) и (2.23) принято, что

масса тела т и соответственно момент инерции привода J являются постоянными, что справедливо для значительного числа производственных механизмов.

Из анализа (2.23) видно:

1) при М > М_с dω/dt > 0, т. е. имеет место ускорение привода;

2) при М < М_с dω/dt < 0, т. е. имеет место замедле­ ние привода (очевидно, что замедление привода может быть и при отрицательном значении момента двигателя);

3) при М = М_с dω/dt = 0; в данном случае привод работает в установившемся режиме.

Вращающий момент, развиваемый двигателем при ра­боте, принимается положительным, если он направлен в сторону движения привода. Если он направлен в сторо­ну обратную движению, то он считается отрицательным.

Отметим, что знак минус перед М_с указывает на тормозя­щее действие момента сопротивления, что отвечает усилию резания, потерям трения, подъему груза, сжатию пру­жины и т. п. при положительном знаке скорости.

При спуске груза, раскручивании или разжатии пру­жины и т. п. перед М_С ставится знак плюс, поскольку в этих случаях момент сопротивления помогает вращению привода.

Инерционный (динамический) момент (правая часть уравнения моментов) проявляется только во время переходных режимов, когда изменяется скорость привода. При ускорении привода этот момент направлен против движения, а при торможении он поддерживает движение. Инерционный момент как по значению, так и по знаку определяется алгебраической суммой моментов двигателя и момента сопротивления.

При учете сказанного о знаках моментов формула (2.23) соответствует работе двигателя в двигательном режиме при реактивном моменте сопротивления (или при потен­циальном тормозящем моменте сопротивления). В общем виде уравнение движения привода может быть записано следующим образом:

(2.23a)

Выбор знаков перед значениями моментов в (2.23а) зависит от режима работы двигателя и характера моментов сопротивления.