8. 3. Переходные процессы при

экспоненциальной зависимости управляющего воздействия

а) Общие положения. Форсирование процесса возбуждения

Экспоненциальная зависимость управляю- щего воздействия характерна для системы Г—Д, в которой закон изменения ЭДС генератора обусловлен индуктив- ностью его обмотки возбуждения. Пуск, торможение и ре- версирование, а также регулирование угловой скорости двигателя в системе Г—Д производят обычно путем соот- ветствующих переключений в цепи обмотки возбуждения генератора, а иногда и двигателя. Так как обмотки воз- буждения обладают сравнительно большой индуктивно- стью, то их электромагнитные постоянные времени велики и переходные процессы в цепях возбуждения машин про- текают сравнительно медленно.

Для обмоток якорей электрических машин значение электромагнитной постоянной лежит обычно в пределах сотых и даже тысячных долей секунды, и поэтому в боль- шинстве расчетов переходных режимов она может не учи- тываться. Что касается обмоток возбуждения машин, то их постоянная времени Т_в имеет уже существенное значение, так как ее значение колеблется в пределах от десятых долей секунды для машин малой мощности до нескольких се- кунд в мощных электрических машинах. Ниже дается представление о порядке электромагнитных постоянных времени в зависимости от мощности машин постоянного тока:

Мощность машины, кВт Постоянная времени обмотки

возбуждения Т_в, с (ориентировочно)

1, 5 0, 2

15 0, 6

75 0, 8 — 0, 9

3000 и выше 2 — 4

Рассмотрим некоторые способы ускорения процесса возбуждения на примере системы Г—Д применительно к мощным реверсивным станам, устанавливаемым для прокатки металла на заводах металлургической промыш- ленности. Выводы, полученные в результате этого расс- мотрения, являются общими для подобных приводов посто- янного тока.

По технологическим условиям в указанных прокатных станах требуется производить 15—20 реверсов в минуту. Как видно из приведенных данных, электромагнитная по- стоянная времени обмотки возбуждения генератора Т_в достигает в некоторых случаях значений, лежащих в преде- лах 2—4 с, и поэтому без специальных мер в подобной уста- новке можно получить лишь три-четыре реверса в минуту.

На рис. 8. 8 показана принципиальная схема Г—Д. Прежде всего рассмотрим процесс нарастания тока в цепи обмотки возбуждения генератора. После замыкания клю- ча К и скачкообразного приложения напряжения к выво-

Рис. 8. 8. Принципиальная схема соединения машин в системе генера- тор — двигатель.

дам обмотки возбуждения ток в ней будет нарастать плавно по экспоненциальному закону ¹:

(8.18)

здесь I_в, _ном = U_в.ном/R_в — установившийся (номинальный) ток в обмотке возбуждения генератора; Т_в — L_в/R_в — электромагнитная постоянная времени этой обмотки; (U_в.ном, R_в и L_в — соответственно номинальное напряжение на выводах обмотки возбуждения, ее активное сопротивле- ние и индуктивность.

Практически процесс возбуждения можно считать за- кончившимся, когда i_в = 0, 95 I_в,иом. В этом случае t_0,95 = = 3Т_в.

Таким образом, приходим к выводу, что скорость элект- ромагнитного процесса возбуждения в указанной схеме определяется постоянной времени обмотки возбуждения генератора.

Для ускорения электромагнитного процесса применя- ются способы, основанные на том, что на время пуска к об-

¹ Здесь и в дальнейшем индуктивность цепи обмотки возбуждения принимается постоянной,

моткам возбуждения генератора прикладывается повышен- ное напряжение. Для ограничения установившегося тока номинальным значением I_в,_ном приходится включать до- полнительный резистор или прибегать к другим мерам ограничения напряжения в установившемся режиме.

На рис. 8. 9 представлена схема с постоянно включенным . дополнительным резистором R_доб. Сопротивление этого резистора подбирается так, чтобы при повышенном напря- жении U'_в > U_в.ном ток в обмотке возбуждения не превос- ходил номинального значения, которое равно:

(8.19)

(8.20)

здесь

где а — коэффициент форсировки, показывающий, во сколь- ко раз приложенное извне напряжение выше номинального;

Рис. 8. 9. Схема цепи возбуждения генератора с постоянно включен- ным дополнительным резистором,

R_р — сопротивление разрядного резистора, принимаемое практически равным (3—4) R_в.

Ток в обмотке возбуждения для рассматриваемой схемы изменяется по закону

(8.21)

где

(8.22)

Анализ (8.22) показывает, что с увеличением R_доб уменьшается постоянная времени цепи возбуждения и, следовательно, более интенсивно возрастает ток возбужде- ния генератора. Очевидно, что с ростом R_доб должно уве- личиваться приложенное напряжение U'_в. Необходимо отметить, как это вытекает из (8. 21), что при t =0, т. е.

в начальный момент процесса возбуждения, i_в = 0 и все внешнее напряжение U'_B прикладывается к выводам об- мотки возбуждения. По мере роста тока возбуждения напря- жение на обмотке возбуждения снижается, достигая уста- новившегося значения. Таким образом, форсировка про-

Рис. 8. 10. Кривые изменения тока возбуждения генератора при различных сопротивлениях Дополнительного резистора в схеме на рис. 8. 9,

цесса возбуждения генератора для рассматриваемой схемы не остается постоянной.

Характер изменения тока возбуждения для этой схемы приведен на рис. 8. 10, где показаны кривые нарастания тока i_B при различных значениях напряжения U'_в и соответ- ственно разных сопротивлениях дополнительных резисто- ров. Совершенно очевидно, что время переходного процесса

Рис. 8. 11. Схема цепи возбуждения генератора с резистором, шунти- руемым на время переходного процесса,

может быть сокращено до требуемого значения. Однако с увеличением сопротивления дополнительного резистора в цепи обмотки возбуждения возрастает и напряжение Ue, а следовательно, и потери в дополнительном резисторе.

Для форсирования процесса возбуждения в системе Г—Д часто применяется схема с шунтированием резистора на время переходного процесса (рис. 8.11).

В подобной схеме напряжение U'_в принимается в нес- колько раз выше номинального, однако ток возбуждения

генератора по-прежнему не должен превосходить номиналь- ного значения. Здесь, как и прежде, коэффициент форси- ровки может быть определен из соотношения α= U´_B/U_B,_ном. Отличие этой схемы от приведенной на рис. 8. 9 заключается в том, что при переходном процессе дополнительный ре- зистор R_доб шунтируется и контакты КФ размыкаются только в момент, когда ток достигает значения I_в.ном. Повы- шенное напряжение в переходных процессах полностью приложено к обмотке возбуждения генератора, а ток i_B стремится к значению I´_B = U'_B/R_B при той же постоянной времени, что и в схеме рис. 8.8.

Рис. 8. 12. Кривые изменения Рис. 8. 13. Кривые изменения

тока i_в = f (t) в схеме с шун- напряжения на выводах обмот-

тируемым резистором, ки возбуждения генератора,

1 — в схеме на рис. 8.9; 2 — в схе- ме на рис. 8.11.

Уравнение для тока возбуждения в переходном режиме имеет следующий вид:

(8.23)

Решением этого уравнения относительно t определяется время, в течение которого ток достигает номинального значения:

(8.24)

Примерные кривые нарастания тока возбуждения при различных коэффициентах форсировки приведены на рис. 8.12. Целесообразно принимать значения коэффициен- та форсировки α = 3 -:- 4, так как дальнейшее его увели- чение мало сказывается на уменьшении времени нараста- ния тока возбуждения.

Сравнивая приведенные выше способы ускорения пере- ходных процессов, можно сделать вывод, что наиболее

эффективным является формирование напряжения, с шун- тируемым на время переходного процесса резистором. Здесь при прочих равных условиях достигается наиболь- шее ускорение процесса и, кроме того, нарастание тока возбуждения идет почти по прямой линии, что благоприятно сказывается на форме кривой тока в цепи якоря двигателя.

Напряжение, прикладываемое к выводам обмотки воз- буждения генератора по схеме, приведенной на рис. 8. 9, уменьшается в процессе пуска (кривая 1 на рис. 8.13), а по схеме, данной на рис. 8.11, остается неизменным, как это показано на рис. 8.13 (кривая 2). Поэтому по схеме, изображенной на рис. 8.11, обеспечиваются более форсиро- ванное нарастание тока возбуждения и большее ускорение переходного процесса при одном и том же напряжении U'_B.

Следует еще раз подчеркнуть, что первопричиной уско- рения переходных процессов во всех рассмотренных выше схемах является увеличение подводимой мощности за счет повышения на время пуска напряжения на выводах обмотки возбуждения генератора. Ускорение процесса возбуждения сокращает длительность переходных режимов двигателя.

б] Пуск электропривода в системе Г—Д

Если принять генератор ненасыщенным, то его ЭДС при ω_г = const будет пропорциональна току воз- буждения и в переходных режимах определится уравне- нием

(8.25)

где Е_ном — номинальное значение ЭДС генератора при

i_в=I_в.ном

Для цепи якоря двигателя, в которой проходит ток i, при пуске уравнение равновесия ЭДС

(8.26)

где R_я и L_я — соответственно сопротивление и индуктив- ность цепи якоря генератора и двигателя; е_Д — ЭДС дви- гателя.

Значение L_я часто можно не учитывать, так как оно мало по сравнению с индуктивностью обмотки возбуждения гене- ратора L_B, т. е. можно принять L_B*di/dt .

Для получения зависимостей, определяющих изменение угловой скорости, тока и момента при пуске двигателя,

необходимо уравнение (8. 26) решать совместно с уравне- нием движения привода:

Полагая при постоянном магнитном потоке двигателя е_Д = сω, а М = ci и решая совместно указанные уравне- ния, получаем зависимость угловой скорости двигателя от времени при пуске:

(8.27)

где ω₀ — угловая скорость идеального холостого хода двигателя; α — коэффициент форсировки; Т_в —- электро- магнитная постоянная времени обмотки возбуждения гене- ратора; Т_м — электромеханическая постоянная времени электропривода; Δω_с — перепад угловой скорости при мо- менте сопротивления М_с, равный

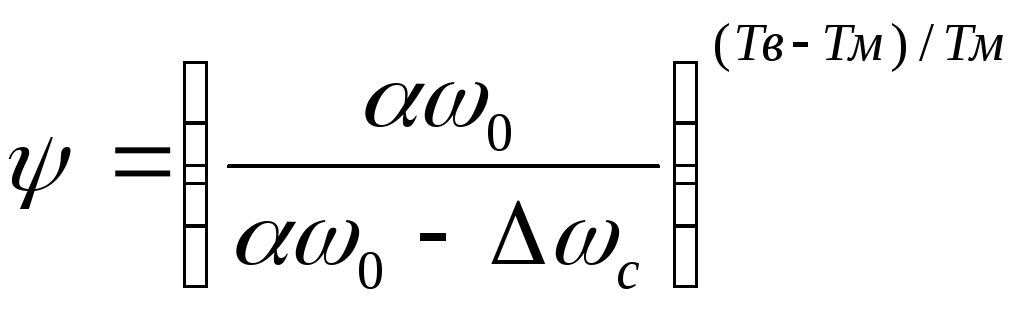(8.28)

Использовав уравнение движения, разделив левую и правую части его на с и взяв производную угловой скорости, из (8.27) можно получить выражение для тока якоря дви- гателя в функции времени:

(8.29)

где I_к, ₃ — ток короткого замыкания в цепи Г—Д, соответ- ствующий номинальному значению ЭДС генератора; I_с — ток нагрузки при моменте сопротивления М_с.

(8.30)

(8.31)

Если пуск двигателя производится без нагрузки, т. е. при M_С = 0, то в этом случае I_с = 0; Δω_с = 0; ψ= 1; тогда

Если магнитный поток двигателя сохраняется неиз- менным, то зависимости для момента, развиваемого дви- гателем, оказываются такими же, как и для тока.

На рис. 8. 14, а, б показаны кривые ω = f (t) и i = f₁ (t) при различных коэффициентах форсировки.

Приведенные выше равенства показывают, что проте- кание переходных процессов в системе Г—Д зависит как ох электромеханической постоянной времени привода Т_м, так и от электромагнитной постоянной времени обмотки возбуждения генератора Т_в. В зависимости от мощности привода эти постоянные имеют различные значения, ле-

жащие в широких пределах. Как упоминалось, в приво- дах мощностью в несколько киловатт Т_в = 0, 1 -:- 0, 3 с.

В мощных приводах ре- версивных прокатных станов Т_в — 2 -:- 4 с, в то время как Г_м = 0, 3 -:- 0, 05 с. В послед- нем случае при определении длительности переходных процессов можно учитывать лишь электромагнитную пос- тоянную времени обмотки возбуждения генератора, пре- небрегая электромеханичес- кой постоянной времени ввиду

Рис. 8. 14. Кривые угловой скоро- сти (а) и тока в цепи якоря (б) при пуске двигателя в системе Г — Д при схеме возбуждения генератора на рис, 8.11.

.

ее относительной малости. Поэтому уравнение (8. 30) примет более простой вид:

(8.32)

При определении зависимости i = f₁ (t) практический интерес представляет нахождение максимального тока в цепи якоря для сравнения его с допустимым значением по условиям коммутации на коллекторе двигателя.

Пользуясь уравнением (8. 29), находим производную di/dt и приравниваем ее 0, т. е.

Отсюда можно определить время, по истечении которого ток достигает максимума, а именно:

(8.33)

Подставив значение t_max в (8.29) и произведя соответ- ствующие преобразования, получим максимум тока в цепи якоря при пуске двигателя

(8.33а)

Если пуск двигателя совершается без нагрузки (М_с = 0, Δω_с = 0 и I_с = 0),

(8.33б)

в) Торможение и реверсирование привода в системе Г—Д

Выше были показаны способы ускорения про- цесса возбуждения и даны соотношения ω = f (t) и i = = f (t) при пуске двигателя постоянного тока в системе Г—Д. Не менее важными являются расчеты, связанные с уменьшением времени переходных процессов при тормо- жении и реверсировании в рассматриваемой системе.

Рис. 8. 15, Схема торможения двигателя в системе Г — Д.

Торможение двигателя М (рис. 8.15) производится чаще всего отключением от сети обмотки возбуждения генератора и замыканием ее на разрядный резистор R_p либо замыка- нием ее на выводы якоря, причем таким образом, чтобы изменялась полярность на обмотке возбуждения. При этом двигатель работает в режиме генератора за счет запасенной в нем и в механической части привода кинетической энер- гии, а генератор — в двигательном режиме. Генератор G, работая двигателем, отдает механическую энергию привод- ному асинхронному (или синхронному) двигателю, связанному с генератором общим валом. Наконец, асинхронный

(или синхронный) двигатель при резком снижении тока возбуждения генератора переходит в генераторный режим, отдавая энергию в сеть переменного тока. Интенсивность спадания тока в обмотке возбуждения характеризует и темп торможения двигателя. Зависимость спадания тока воз- буждения генератора от времени при торможении может быть установлена на основании уравнения

Решение этого уравнения относительно тока i_в дает:

(8.34)

где Т_в = L_B/(R_B + R_р) — электромагнитная постоянная времени контура возбуждения.

По-прежнему полагая генератор ненасыщенным, полу- чаем изменение ЭДС генератора при торможении:

(8.35)

(8.36)

Из приведенных уравнений видно, что уменьшение по- стоянной времени приводит к форсированию процесса тор- можения. Последнее достигается увеличением сопротивле- ния разрядного резистора. Однако следует иметь в виду, что напряжение на выводах разрядного резистора, а зна- чит, и на обмотке возбуждения подчиняется следующему закону:

а при t — О

Значительное увеличение сопротивления разрядного ре- зистора, связанное с уменьшением постоянной времени, может привести к недопустимым перенапряжениям на вы- водах обмотки возбуждения в начале торможения, а также к значительным броскам тока в цепи якоря. Поэтому со- противление разрядного резистора практически не превы- шает обычно трехкратного сопротивления обмотки возбу- ждения.

Для нахождения аналитической зависимости угловой скорости двигателя от времени при торможении решаем совместно два уравнения:

После преобразований получим:

(8.37)

Ток в цепи якорей машин определяем по формуле

(8.38)

(8.39)

или

(8.40)

При М_с = 0

Кривые ω = f (t) и i = f₁ (t) при М_с = 0 приведены соответственно на рис. 8. 16 и 8, 17. Кривые 1на обоих ри-

Рис, 8. 16. Кривые угловой ско Рис. 8-17. Кривые тока в цепи

рости двигателя при торможе- якоря при торможении двигате-

нии двигателя в системе Г —Д ля в системе Г— Д по схеме

по схеме на рис, 8, 15, на рис, 8, 15.

сунках относятся к приводам с большей постоянной вре- мени Т_в, кривые 2 — с меньшей.

Максимум тока при торможении находим из уравнений (8. 31) путем приравнивания 0 производной тока по вре- мени

(8.41)

Если торможение производится без нагрузки (I_С = 0), то

(8.42)

Реверсирование двигателя в рассматриваемой системе осуществляется изменением полярности напряжения, при-.

кладываемого к выводам обмотки возбуждения генератора, что вызывает быстрое спадание тока возбуждения, а затем нарастание его в обратном направлении.

Форсирование возбуждения при реверсировании совер- шается таким же образом, как и при пуске.

Зависимость тока возбуждения от времени определяется из уравнения

(8.43)

(8.44)

После соответствующих преобразований получим:

Электродвижущая сила генератора при ненасыщенной

машине

(8.45)

Решая совместно уравнение равновесия ЭДС для цепи якоря и уравнение движения привода относительно ω, получаем:

(8.46)

Если реверсирование происходит без нагрузки (М_с = 0 и Δω_с = 0), то

(8.47)

Примерные кривые изменения угловой скорости двига- теля при реверсировании для различных коэффициентов форсировки и M_c = 0 представлены на рис. 8. 18.

Воспользовавшись уравнением (8. 47) и подставив в него ω = -ω₀, можно определить длительность реверса, т. е. время, в течение которого угловая скорость ненагружен- ного двигателя изменится от +ω₀ до -ω₀.

Для мощных электроприводов значением Т_м вследствие малости его по сравнению с Т_в можно пренебречь. В этом случае время реверса определится по упрощенной формуле

(8.48)

Формула (8. 48) указывает на то, что продолжительность реверсирования зависит от постоянной времени цепи воз- буждения и коэффициента форсировки.

Если воспользоваться выражением производной угло- вой скорости по времени

и подставить его в уравнение для тока

то после несложных преобразований получим:

(8.49)

При I_с = 0

(8.50)

Кривые изменения тока i = f (t) при I_с = 0 и различ- ных значениях α представлены на рис. 8. 19.

Рис. 8. 18. Примерные кривые Рис. 8. 19. Примерные кривые

угловой скорости при реверси- тока двигателя при реверсиро-

ровании для различных коэф- вании для различных коэффи-

фициентов форсировки (α= 1; циентов форсировки (α = 1; 2

2 и 3). и 3).

По известному правилу нахождения максимума опреде- ляем время, в течение которого ток достигает максималь- ного значения,

(8.51)

и максимум тока

(8.52)

или приI_с = 0

(8.53)

В тех случаях, когда необходимо учитывать насыщение генератора и индуктивность якорной цепи, приходится прибегать к графо-аналитическим построениям или исполь- зовать ЭВМ.

Как было показано, формирование переходных процес- сов в системе управляемый преобразователь—двигатель зависит от инерционности преобразователя. Если учесть . индуктивность якорной цепи системы Г — Д, то оказы- вается невозможным воспроизведение линейного закона на- растания тока в якорной цепи двигателя и поэтому трудно формировать темп нарастания момента.

Хотя формирование линейного нарастания ЭДС преоб- разователя и обеспечивает высокую стабильность макси- мального углового ускорения электроприводов при неиз- менной динамической составляющей момента, и все же в разомкнутой системе угловое ускорение зависит от на- грузки, поэтому ограничивается эффективность формиро- вания переходных процессов в разомкнутой системе, и в случае, если предъявляются более жесткие к ним требо- вания, необходимо создавать замкнутую систему.

Системы замкнутого регулирования скорости и момента для приводов постоянного и переменного тока приводятся в гл. 12.

ГЛАВА ДЕВЯТАЯ

РАСЧЕТ МОЩНОСТИ ЭЛЕКТРОПРИВОДОВ