менения угловой скорости. В результате слияния этих факторов при синхронной угловой скорости двигателя токи ротора могут быть не равны 0, поэтому соответственно момент двигателя не равен 0, и ротор разгоняется до угловой скорости, превышающей синхронную. Далее, токи ротора уменьшаются, уменьшается момент, развиваемый двигателем, а значит, уменьшается угловая скорость и т, д. Поэтому в конце переходного процесса пуска изменения угловой скорости и

момента двигателя имеют затухаю- щий колебательный характер. Чем мягче рабочий участок статичес- кой механической характеристики и чем больше момент инерции ро- тора, тем меньше амплитуда этих колебаний и тем быстрее они зату- хают. Практически колебания уг-

Рис. 7. 38. Статическая характери- стика ω =f(I₂) асинхронного дви- гателя.

ловой скорости и момента двигателя в конце переходного процесса пуска наблюдаются не всегда.

Итак, анализ электромагнитных переходных процессов на при- мере пуска двигателя показывает, что в начале переходного процесса момент двигателя определяется переходными токами, обусловленными в основном коммутационными операциями, а в конце переходного процесса зависимость М (t) определяется соотношением механической инерции ротора (момент инерции ротора) и электромагнитной инерции, связанной с индуктивностями обмоток асинхронной машины.

Изучение электромагнитных переходных процессов в асинхрон- ном двигателе имеет теоретическое и практическое значение, поскольку, как показано выше, исключение из рассмотрения их влияния иска- жает действительное представление о характере переходных процессов в асинхронном электроприводе. Исследования показывают, что мак- симальные значения переходного момента могут существенно превы- сить номинальный момент двигателя: при пуске в 2—4 раза, при ре- версировании в 8—15 раз, что. следует учитывать при анализе свойств конкретного электропривода.

ГЛАВА ВОСЬМАЯ

ФОРМИРОВАНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ

8. 1. Общие положения

. Ранее было показано (см. гл. 7), как возни- кающие переходные процессы протекают в электроприводе при изменении управляющего воздействия скачком. В этом случае рассматривались условия пуска, торможения, ре-

версирования, перехода от одной угловой скорости к дру- гой при моментах двигателей постоянного и переменного тока, зависящих от угловой скорости. Однако условия ра- боты производственных механизмов требуют от электро- привода обеспечения соответствующего формирования пе- реходных режимов, направленного на достижение либо максимального быстродействия, либо минимума потерь, либо ограничения динамических нагрузок, возникающих в элементах кинематических цепей, связывающих электро- привод с рабочим органом машины, и т. д. Управление переходными процессами электропривода может создать максимальное быстродействие при соответствующих огра- ничениях. Например, для двигателя постоянного тока

Рис. 8. 1. Графики зависимости угловой скорости, углового уско- рения и производной углового ускорения от времени, обеспечива- ющие ограничение динамических нагрузок привода.

одно из таких ограничений состоит в том, что ток в якоре не должен по условиям коммутации превосходить 2—2,5- кратного значения номинального. Другим ограничением, например при отработке заданного перемещения, является недопустимость превышения некоторого максимального зна- чения угловой скорости, определяемого условиями коммута- ции и механической прочностью якоря.

В большинстве случаев надо так формировать переход- ные процессы, чтобы ограничивать угловое ускорение привода, т. е. первую производную угловой скорости dω/dt, и ограничивать вторую производную угловой ско- рости ρ = d²ω/dt² (рывок) или первую производную мо- мента двигателя dM/dt = Jd²ω/dt² при М_С = const. В ка- честве примера можно сослаться на электропривод лифта, где необходимо ограничить ускорение, превышение кото- рого неблагоприятно сказывается на самочувствии пасса- жиров и важно для снижения динамических усилий в ка-

натах и кабине лифта. Максимальные значения ускорений и замедлений при движении кабины не должны превышать 1,5—2 м/с², производная ускорения и замедления для ско- ростных лифтов 3—10 м/с³.

Графики зависимости угловой скорости, углового ус- корения (или пропорционального ему тока при М_с = 0) и производной углового ускорения от времени, обеспечиваю- щие требуемое ограничение динамических нагрузок, при- ведены на рис. 8. 1.

Вкратце рассмотрим формирование переходных процес- сов для двух практических случаев: 1) при линейном за- коне нарастания управляющего воздействия на выходе преобразователя; 2) при экспоненциальном возрастании управляющего воздействия, характерном для системы Г—Д и обусловленном инерционностью обмотки возбуждения- генератора.

8. 2. Формирование переходных процессов при линейном нарастании управляющих воздействий

Линейный закон нарастания управляющего воздействия достигается при использовании тиристорного преобразователя, практически являющегося безынерцион- ным, поэтому линейное изменение ЭДС на его выходе по- лучают путем подачи на вход системы управления преоб- разователем сигнала, изменяющегося во времени линейно. Закон изменения ЭДС преобразователя, или, что то же самое, угловой скорости идеального холостого хода ω₀ двигателя постоянного тока независимого возбуждения представлен на рис. 8. 2, б и определяется формулой

(8.1)

где ε_п — угловое ускорение электропривода при пуске, характеризующее темп изменения ω₀.

Примем, что ε_п имеет такое достаточно малое значение, которое позволяет пренебречь влиянием на переходный процесс электромагнитной инерции (индуктивности якор- ной цепи).

а\ Пуск привода вхолостую

Примем механические характеристики ли- нейными и параллельными друг другу при различных фиксированных значениях ЭДС (рис. 8. 2, а) и номинальном

магнитном потоке (Ф_ном = const), т. е.

(8.2)

где β = (kФ_ном)²/R_яΣ = ΔM/ | Δ ω | — абсолютное значе- ние жесткости механической характеристики.

Рис. 8. 2. Механические ха- рактеристики привода (а) и графики переходных процес- сов (б, в) при пуске вхолос- тую.

Если принять, что статический момент М_с = 0, то уравнение движения привода можно представить в виде

Используя (8. 1), (8. 2) и уравнение движения, получаем дифференциальное уравнение переходного процесса:

(8.3)

Кривая ω (t), получаемая в результате решения (8. 3), имеет два участка, для каждого из которых расчет необ- ходимо вести отдельно. Для первого участка (до t_n0 на рис. 8. 2, б, в), принимая при t = 0 ω_нач = 0, получаем:

(8.4)

Это выражение графически показано на рис. 8. 2, б.

Воспользовавшись уравнением движения (при М_с = 0), получим показанное на рис. 8. 2, в изменение момента во времени:

(8.5)

Момент при t ≥ 3T_М достигает практически своего мак- симального (установившегося) значения, и соответственно угловое ускорение остается постоянным, а угловая скорость изменяется с таким же темпом, как и вызвавшая рассмат- риваемый переходный процесс ЭДС преобразователя.

Максимальное значение момента, равное М_тах = Jε_п, дает возможность оценить допустимое значение ε_п.

На рис. 8. 2, а утолщенной линией показана зависимость ω = f(М) в переходном режиме (фазовая траектория про- цесса), отражающая динамическую механическую харак- теристику привода.

(8.6)

где ω_нач = ω_А = ω_А1 (рис. 8. 2, а, б);

(8.7)

Второй этап пуска (при Т ≥ t_п0 на рис. 8. 2, б, в) проис- ходит тогда, когда ЭДС преобразователя и соответствую- щая ей угловая скорость идеального холостого хода по прошествии времени t_п0 окажутся постоянными. Для этого этапа пуска угловую скорость и момент двигателя удобно рассчитывать, вводя новый отсчет времени с t_п0 и обозначая время через t' = t — t_п0. Тогда на втором участке пуска угловую скорость и момент можно записать следующим образом:

т. е. переходный процесс в данном случае протекает так, как это имеет место при линейной механической характе- ристике двигателя и отсутствии момента нагрузки (М_С = 0), что соответствует участку Аω₀₁ на рис. 8. 2, а. На рис. 8. 2, б показан участок разгона привода от точки А1 до угловой скорости ω₀₁, построенный в соответствии с (8. 6), и, нако- нец, на рис. 8. 2, в дано изменение момента М (t) по урав- нению (8. 7) при разгоне привода.

б] Пуск привода с реактивным моментом нагрузки

Используя уравнение движения, линейность механической характеристики двигателя и закона изме- нения ЭДС преобразователя, получаем дифференциальное

(8.8)

уравнение переходного процесса пуска привода под на- грузкой:

где Δω_с = перепад угловой скорости на механической характеристике двигателя, обусловленный моментом нагруз- ки; ω_с (t) = ε_пt — Δω_c.

Если момент нагрузки является реактивным, то дви- гатель остается неподвижным до тех пор, пока момент, раз- виваемый им, не станет равным М_с. На этом этапе переход- ного процесса, если двигатель подключен к преобразо- вателю, ток и соответственно момент изменяются по прямой

Рис. 8. 3. Механические характеристики (а) и графики переходных процессов (б) при пуске под нагрузкой с реактивным моментом.

линии до значения М_с = ε_пt₀ | β |. С момента времени t₀ (ε_пt₀ = Δω_c), называемого временем запаздывания, мо- мент двигателя становится М > М_с, и происходит пуск электропривода по характеристике (по фазовой траектории), показанной утолщенной линией на рис. 8. 3, а.

Переходный процесс на втором участке начинается с t₀ и продолжается до t_пl (рис. 8. 3, б). Вводя новый отсчет времени и обозначая его t' — t— t₀, уравнение (8. 7) запи- сываем в виде

(8.9)

Полное решение этого уравнения с учетом того, что при t' = 0 угловая скорость ω = 0, а постоянная интегриро-

вания С = Т_Мε_п, имеет вид:

(8.10)

Уравнение (8. 10) описывает переходный процесс на втором участке, причем первая составляющая представ- ляет линейно-изменяющуюся угловую скорость в том же темпе, что и ω₀ (t). Вторая составляющая изменяется по экспоненте, и через время, практически равное 3Т_М, угло- вая скорость нарастает линейно, т. е.

(8.11)

Момент двигателя

(8.12)

В начале второго участка момент так же, как и угловая скорость, изменяется по экспоненте. По истечении времени t' ≈ 3Т_М он практически достигает максимального значе- ния и остается постоянным (рис. 8. 3, б).

На третьем участке при t> t_п1, где ω₀ (t) = ω₀₁ и угло- вая скорость электропривода достигает установившегося значения ω_с = ω₀₁ — Δω_с, дифференциальное уравнение переходного процесса принимает вид:

(8.13)

где t" = t — t_п1.

Решение уравнения (8. 13):

Момент двигателя

здесь ω_нач, М_тах равны соответственно значениям угловой скорости и момента в конце второго этапа переходного процесса.

Из рис. 8. 2 и 8. 3 следует, что характер переходных про- цессов в основном зависит от темпа нарастания ЭДС пре- образователя и не зависит от статического момента. От этого темпа зависит динамический момент, создающий ускорение привода.

При заданном значении динамического момента угловое ускорение (темп нарастания ЭДС преобразователя) опре- деляется моментом инерции привода:

(8.14)

в) Пуск привода с активным моментом нагрузки

Переходный процесс пуска с активным момен- том нагрузки определяется начальными условиями на пер- вом этапе. Допустим, что ω_нач = 0, ω₀ = ε_пt, перепад угловой скорости, обусловленный активным моментом на- грузки, не меняющим своего знака, составляет —Δω_с> как показано на рис. 8. 4, а. Тогда по аналогии с предыдущим,

Рис. 8. 4. Механические характеристики (а) и графики переходных про- цессов (б) при пуске с активным моментом нагрузки,

подставив начальные условия, получим уравнение для скорости привода:

(8.15)

Производная скорости равна:

при t= 0

Это означает, что момент нагрузки, будучи активным, заставляет привод вращаться в обратную сторону. При t > 3T_М

ускорение dω>/dt — ε_п, т. е. привод разгоняется.

Графики изменения скорости и момента во времени показаны на рис. 8. 4, б.

г) Торможение привода под нагрузкой

(8.16)

При наличии момента нагрузки торможение начинается с угловой скорости ω_с, соответствующей мо- менту М_с (рис. 8. 5, а). Для первого этапа торможения (до ω₀ = 0) можно записать уравнение

где —ε_т — угловое замедление привода при торможении (темп спадания ЭДС преобразователя), в частном случае ׀ ε_т | = ε_п.

Рис. 8. 5. Механичес- кие характеристики (а) и графики переходных процессов (б, в) при торможении с реактив- ным и активным мо- ментами нагрузки.

(8.17)

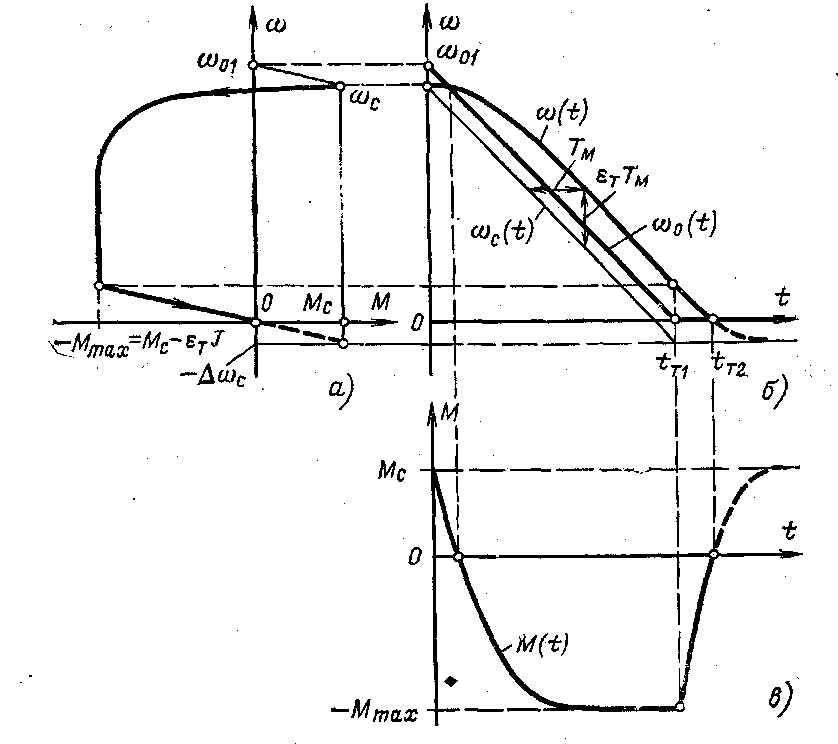
Момент двигателя

На втором этапе, начиная со времени t_т1, когда двига- тель выходит на статическую характеристику с ω_q = 0 при условии, что момент нагрузки реактивный, угловая скорость и момент изменяются по экспоненте соответственно до значений ω = 0 и М = 0, так как реактивный момент

сопротивления не вызывает движения. Графики переход- ных процессов показаны на рис. 8. 5, б, в, а фазовая траек- тория — на рис. 8. 5, а.

Торможение с активным моментом нагрузки не отли- чается вплоть до ω = 0 от случая, рассмотренного выше, когда момент нагрузки являлся реактивным. При активном моменте нагрузки (как показано штриховой линией на рис, 8. 5) привод реверсируется начиная со времени t_т2 до угловой скорости, равной -Δω_с, за счет статического момента, который не изменяет своего знака при изменении направления вращения двигателя. Момент двигателя до- стигает значения, равного моменту сопротивления.

д) Реверсирование привода под нагрузкой

Изменение направления вращения привода должно осуществляться изменением знака ЭДС преобра- зователя (или ω₀) от положительного значения до отрица- тельного; при этом, если считать момент нагрузки актив-

Рис. 8. 6. Механические характеристики (а) и график переходного про- цесса (б) при реверсировании с активной нагрузкой на валу,

ным, т. е. не меняющим своего знака при переходе через нулевое значение угловой скорости, угловое ускорение привода на всем этапе реверсирования остается постоянным, как это видно из рис. 8. 6, а, б. Переходный процесс на пер- вом этапе до угловой скор ости, близкой к установившейся, не отличается от процесса при торможении с активным моментом. На втором этапе, когда двигатель выходит на статическую характеристику, переходный процесс имеет

экспоненциальный характер и угловая скорость возрастает (по абсолютной величине) до установившегося значения ω= -ω_с2.

Переходный процесс при реверсировании привода с ре- активной нагрузкой на его валу протекает сложнее в связи с тем, что при переходе угловой скорости через 0 реактив- ный момент меняет скачком свой знак. Разгон привода в противоположную сторону происходит при условии, что момент, развиваемый двигателем, по абсолютному значению превосходит статический момент.

Рис. 8. 7. Механические характеристики (а) и график переходного про- цесса (б) при реверсировании с реактивной нагрузкой на валу.

Процесс торможения до угловой скорости, равной 0 (первый этап реверса привода), протекает так же, как и в случае реверса с активным моментом нагрузки, до точки t_р1 (рис. 8. 7).

На втором этапе в случае, если при ω = 0 | М \ > | М_с |, начинается разгон в обратную сторону. Так как в первый момент при t = t_pl динамический момент оказывается мень- ше, чем он был в период торможения, то в точке перехода через нулевое значение угловой скорости угловое ускорение привода по абсолютному значению становится меньшим. Поэтому для сохранения заданного углового ускорения ε_т нужно увеличить динамический момент привода, т. е. на втором этапе изменение угловой скорости ω(t) связано с возрастанием динамического момента (рис. 8, 7). На треть- ем этапе (точка t = t_p2) в соответствии с линейной характе- ристикой двигателя (-М_тах, -ω₀) угловая скорость и момент привода изменяются по экспоненте.