7.4. Динамическое торможение двигателя постоянного тока независимого возбуждения

Если обмотку якоря работающего двигателя посредством переключателя К отключить от сети и замкнуть на дополнительный резистор R₁ (рис. 7.13), то двигатель переходит в генераторный режим динамического торможе­ния и снижает свою угловую скорость (рис. 7.14).

Обмотка возбуждения в процессе торможения остается присоединенной к сети постоянного тока.

Основные уравнения, характеризующие процесс динами­ческого торможения:

сω + iR = 0; (7.42)

ci = J +M_c ,

где R = R₁ +R_я .

Совместное решение этих уравнений относительноω дает:

ω = — Δω_c + C , (7.43)

Постоянная интегрирования С определяется из началь­ных условий. При t = 0

ω = ω_нач = ω_с ;

С = ω_нач + Δω_с ,

где ω _нач = ω_с — угловая скорость двигателя в момент пе­реключения с двигательного режима на динамическое тор-

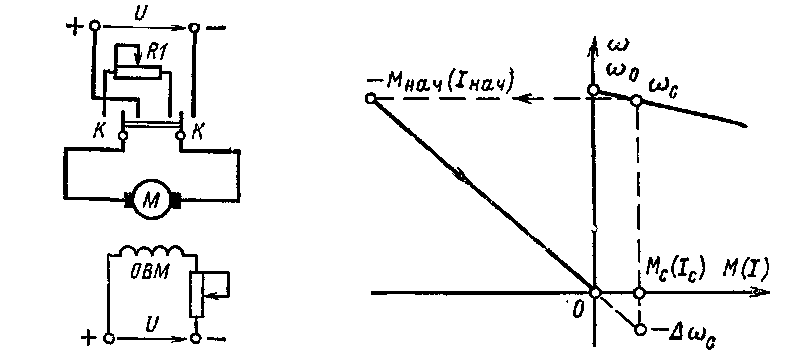
Рис. 7.13. Принципиаль­ная схема динамического торможения двигателя по­стоянного тока независи­мого возбуждения.

Рис. 7.14. Механические характерис­тики двигателя постоянного тока неза­висимого возбуждения при переходе из двигательного режима в режим динамического торможения.

можение; Δω_с = M_cR/c² — абсолютное значение перепада угловой скорости, определяемое по характеристике дина­мического торможения при моменте нагрузки М_с (рис. 7.14). После подстановки значения С в (7.43) получим:

ω = — Δω_с + (ω _нач + Δω_с) . (7.44)

При динамическом торможении без нагрузки (М_с = 0) Δω_с = 0 и ω _нач = ω₀, тогда

ω= ω₀ . (7.45)

На рис. 7.15, а показаны характеристики ω = f (t) при динамическом торможении в случае, когда торможение производится под нагрузкой (кривая 1) и когда М_с = 0 (кривая 2).

При торможении под нагрузкой кривая ω = f (t) асим­птотически стремится к угловой скорости —Δω_с, если момент нагрузки активный, например, в случае опускаю­щегося груза в приводе крановой установки. Если момент нагрузки реактивный, то торможение электропривода за­кончится при угловой скорости ω = 0 (точка b).

При торможении без нагрузки кривая ω = f (t) асимп­тотически приближается к 0, начальная угловая скорость в атом случае ω _нач = ω ₀.

Рис. 7.15. Кривые ω = f (t) (а) и i = f₁ (t) (б) при динамическом тор­можении двигателя постоянного тока независимого возбуждения.

Для определения i = f₁ (t) можно воспользоваться фор­мулой (7.8), если подставить в нее постоянную интегриро­вания С, соответствующую данным начальным условиям

С = сT_м(I_нач + I_с) /J.

Тогда

i = – (I_нач + I_с) +I_с . (7.46)

На рис. 7.15, б кривая 1 иллюстрирует изменение тока в цепи якоря при динамическом торможении и наличии активной нагрузки на валу двигателя, которой соответст­вует ток I_с. При реактивном моменте процесс закончится в точке b при ω = 0.

Кривая 2 иллюстрирует процесс динамического тормо­жения при М_с — 0. Ток в цепи якоря для этого случая определяется по формуле

i = –I_нач , (7.47)

Абсолютное значение тока в момент переключения из двигательного режима в режим динамического торможения

I_нач = сω_нач/R. (7.48)

Время торможения от начальной угловой скоростиω_нач до текущей ω₁ может быть получено из (7.44), если решить его относительно t₁ т. е.

t₁ = Т_м ln (7.49)

При торможении до полной остановки (ω₁ = 0)

t_т = Т_м1n (7.50)

Когда I_с = 0; Δω_с = 0 и теоретически время t_т = ∞, практически процесс торможения можно считать закон­ченным за время t_т = 3T_М. Постоянная времени определя­ется аналогично тому, как это производилось в § 7.2. В дан­ном случае учитывается суммарное сопротивление цепи якоря двигателя при динамическом торможении.

Время торможения может быть также определено на основании (7.46). Например, при торможении до полной остановки, когда i = 0, время торможения

t_т = Т_м1n (7.51)