ГЛАВА СЕДЬМАЯ

ПЕРЕХОДНЫЕ РЕЖИМЫ В ЭЛЕКТРОПРИВОДАХ

7.1. Общие положения

Переходным или динамическим режимом элек­тропривода называется режим работы при переходе из одного установившегося состояния привода к другому, происходящему во время пуска, торможения, реверсиро­вания и резкого приложения нагрузки на валу. Эти режимы характеризуются изменениями ЭДС, угловой ско­рости, момента и тока.

Изучение переходных режимов электропривода имеет большое практическое значение. Результаты их расчетов позволяют правильно определить мощность электродви­гателей и аппаратуры, рассчитать систему управления и оценить влияние работы электропривода на производи­тельность и качество работы производственных механиз­мов.

В переходном режиме электропривода одновременно и взаимосвязано между собой действуют переходные меха­нические, электромагнитные и тепловые процессы. При быстро протекающих процессах изменение теплового со­стояния электропривода в большинстве случаев не оказы­вает существенного влияния на другие процессы, поэтому в дальнейшем при изучении переходных режимов в электро­приводах изменение теплового состояния двигателя не учитывается. В этом случае имеют в виду протекание только механических и электромагнитных переходных процессов, в совокупности называемых электромеханическим пере­ходным процессом.

Электромагнитные переходные процессы вызываются электромагнитной инерцией обмоток электрических машин и аппаратов. В некоторых случаях с влиянием электромаг­нитных процессов можно не считаться, тогда переходные процессы будут определяться только механическими про­цессами, в которых учитывается только механическая инерция движущихся масс электропривода.

При расчете переходных процессов необходимо построить зависимости i = f₁(t); М = f₂(t); ω = f₃(t), а в ряде случаев зависимость пути от времени φ = f₄ (t).

7.2. Пуск двигателя постоянного тока независимого возбуждения до основной угловой скорости и ударное приложение нагрузки

Переходный процесс пуска двигателя посто­янного тока независимого возбуждения до основной ско­рости происходит в случае питания двигателя от сети постоянного тока при замыкании в цепи якоря выключа­теля К (рис. 7.1). В приведенной схеме постоянно включен резистор, следовательно, общее сопротивление цепи якоря

R =R_я+R_p .

При исследовании процесса пуска полагаются неизмен­ными: магнитный поток двигателя Ф, напряжение сети U

Рис. 7.1. Принципиальная схе- Рис, 7.2. Пусковая механичес

ма пуска двигателя постоянного кая характеристика двигателя

тока независимого возбуждения постоянного тока независимого

в одну ступень. возбуждения.

и момент нагрузки M_c. Кроме того, индуктивность обмотки якоря принимается L_я = 0.

Уравнения электрического и механического равновесия системы при пуске:

U=cω + iR; (7.1)

M = ci = J +M_C. (7.2)

Если из (7.2) определить значение тока якоря i и под­ставить его в (7.1), а затем разделить его левую и правую части на с, то после несложных преобразований получим:

(7.3)

или

где ω₀ = U/с — угловая скорость двигателя при идеаль­ном холостом ходе; Δω_с = M_сR/с² — перепад угловой скорости при нагрузке моментом М_с (рис. 7.2); Т_M = JR/с² = = Jω₀/M_K,3 — электромеханическая постоянная времени.

Электромеханической постоянной времени называется время, в течение которого привод, обладающий моментом инерции J, разгоняется без нагрузки из неподвижного состояния до угловой скорости идеального холостого хода ω₀ при неизменном моменте, равном моменту короткого замыкания M_K,3. Необходимо отметить, что постоянная времени зависит от М_K,3. С увеличением сопротивления цепи якоря момент М_K,3 уменьшается и соответственно увеличивается постоянная времени. Электромеханическая постоянная времени не зависит от нагрузки.

Уравнение (7.2) может быть записано иначе:

d ω/dt + ω/T_м = (ω₀ — Δω_с)/T_м . Решение этого уравнения дает:

ω = ω₀ — Δω_с+ С, (7.4)

где С — постоянная интегрирования, определяемая по начальным условиям переходного режима.

Для t = 0 начальное значение угловой скорости ω = = ω_нач, поэтому

С = ω_нач — (ω₀ — Δω_с) = ω_нач — ω_c .

Теперь легко получить уравнение для угловой скорости двигателя при пуске в общем виде:

ω = ω_с + (ω_нач — ω_с) , (7.5)

где ω_с — установившаяся угловая скорость двигателя при моменте нагрузки М_с (рис. 7.2).

В частном случае, когда пуск двигателя совершается под нагрузкой из неподвижного состояния (ω_нач = 0),

ω = ω_с (1-). (7.6)

При пуске без нагрузки до установившейся угловой скорости ω₀

ω = ω_о(1-). (7.7)

Аналогичные формулы получаются, если вместо угло­вой скорости использовать частоту вращения двигателя п, об/мин, приводимую в каталогах.

На рис. 7.3 представлены кривые ω = f(t) при пуске двигателя постоянного тока независимого возбуждения под нагрузкой (кривая 1) и без нагрузки (кривая 2). Со­гласно (7.6) и (7.7) процесс пуска теоретически заканчи­вается за бесконечно большое время. Однако практически можно считать процесс пуска закончившимся при t_n = = (3÷4) Т_M , так как угловая скорость в этом случае отличается от установившегося значения не более чем на 5—2 %. Из (7.6) вытекает, что

при t =∞; = 0; ω = ω_с;

» t = ЗТ_м ; е^-з ≈ 0.05; ω ≈ 0,95 ω _с;

» t = 4Т_м ; е^-4 ≈ 0,02; ω ≈ 0,98 ω _с.

Таким образом, для t = 3 Т_M угловая скорость привода отличается от установившегося значения не более чем на 5 %, и можно считать, что неустановившийся процесс к этому времени практически закончится.

Если бы пуск двигателя совершался с неизменным мо­ментом, равным М_к,₃, то уг-

Рис. 7.3. Кривыеω = f(t) при пуске двигателя постоянного тока независимого возбуждения в одну ступень.

ловая скорость двигателя во времени изменялась бы по прямой Оа при пуске двигателя без нагрузки и по Об — при пуске под нагрузкой (рис. 7.3). Следовательно, если провести через начало координат касательную к кривой 2 до пересечения с горизонталью, проходящей через точку ω₀, то полученный отрезок ω₀а даст в определенном масштабе значение t=T_M. Если же аналогичным путем провести касательную к прямой 1, то отрезок ω_сб также будет равен Т_M .

Зависимость тока в цепи якоря от времени при пуске двигателя определяется из (7.2):

где I_с = M_c /c — ток нагрузки.

Определив из (7.4)

иподставив значение производной в уравнение для тока, получим:

(7.8)

Для начальных условий при t = 0; i = I_нач постоянная интегрирования

Подставив постоянную интегрирования С в (7.8), най­дем:

i=I_c+(I_нач – I_с) . (7.9)

Начальное значение тока в общем виде определяется по формуле

I_нач = (U-E)/R.

В частном случае, когда пуск совершается из неподвиж­ного состояния двигателя, ЭДС его равна 0 и I_нач = I_к,3 = U/R.

Ток в якоре при этом выражается зависимостью

i = (I_к,з – I_с) + I_с. (7.10)

При пуске без нагрузки, когда I_с = 0,

i= I_к,з . (7.11)

По (7.10) и (7.11) построены кривые i= f(t), приве­денные на рис. 7.4.

Из рассмотрения (7.5), (7.6), а также (7.10) и (7.11) можно заключить, что если механическая характеристика двигателя линейна и момент нагрузки постоянен, то ω =

= f(t) и i = f₁(t) выражаются простыми экспоненциаль­ными зависимостями.

При многоступенчатом резисторном пуске двигателя постоянного тока независимого возбуждения и постоянном напряжении сети задаются обычно определенными грани­цами колебаний пускового тока или пускового момента. В этом случае для нахождения времени пуска удобнее пользоваться в качестве исходного не уравнением угловой скорости, а уравнением тока (7.9).

Процесс пуска двигателя в несколько ступеней, изобра­женный на рис. 7.5, характерен тем, что ток двигателя во время пуска колеблется в пределах от I₁ до I₂. В начале пуска I_нач = I₁, далее по мере ускорения двигателя рас­тет его ЭДС, вследствие чего начинает уменьшаться ток в цепи якоря двигателя, а следовательно, и момент двига­теля. Когда ток достигнет некоторого значения I₂, выклю­чается часть пускового резистора с таким расчетом, чтобы ток двигателя снова достиг значения I₁ и т. д. Найдем

Рис. 7.4. Кривые i = f (f) при пуске двигателя постоянного тока независимого возбуждения в одну ступень.

1 — пуск под нагрузкой; 2 — пуск вхолостую.

Рис. 7.5. Графики при реостат­ном пуске двигателя постоян­ного тока независимого воз­буждения в несколько ступе­ней.

время t_x, в течение которого ток двигателя изменяется от I₁ до I₂. Для этого воспользуемся уравнением (7.9), написав его в следующем виде:

I₂ = I_c+(I₁ – I_с) , (7.12)

где I₁ и I₂ — границы изменения пускового тока (рис. 7.5); t_x — время разбега двигателя на рассматриваемой ступени пускового резистора; Т_M,х — электромеханическая пос­тоянная времени для той же ступени.

Постоянная времени для каждой ступени резистора соответствует суммарному сопротивлению цепи якоря.

Решая (7.12) относительно времени разбега, находим:

(7.13)

Если значение тока нагрузки Iс не изменяется, то под знаком логарифма стоит постоянная величина и, следова­тельно, можно написать:

t_x = kT_MX. (7.14)

По мере выведения резистора сопротивление цепи якоря уменьшается, а следовательно, уменьшается и электроме­ханическая постоянная времени, что приводит в свою очередь к уменьшению времени разбега на каждой после­дующей ступени,

т. е. t_xl > t_x2 > t_X3 и т. д.

Приведенная на рис. 7.5 зависимость i = f (t) построе­на на основании (7.9) с учетом сказанного выше, а кривая угловой скорости двигателя ω = f (t) построена по (7.5). Время переходного процесса на последней ступени (при I = I_с или ω = ω_с) получается равным бесконечности

Рис. 7.6. Графики ω = f (t) и i = f (t) при пуске в одну ступень под нагрузкой двигателя постоян­ного тока независимого возбужде­ния, построенные с учетом элект­ромагнитной инерции якоря.

Практически для этой ступени надо принимать подобно предыдущему

t_x = (3÷4) T_мx .

В тех случаях, когда время протекания электромагнит­ных процессов соизмеримо со временем протекания механи­ческих процессов, приходится учитывать и влияние элект­ромагнитной инерции цепи якоря, которым мы до сих пор пренебрегали. На рис. 7.6 показаны кривые пуска дви­гателя при постоянном напряжении сети и учете индуктив­ности якоря. Как видно из рис. 7.6, пуск двигателя состоит из двух этапов.

Первый этап: якорь двигателя неподвижен, пока ток в якоре не достигнет значения, необходимого для создания момента трогания. На этом этапе увеличение тока двига­теля зависит от скорости протекания электромагнитного

процесса, определяемого уравнением напряжений для цепи якоря двигателя:

U = iR + L_я . (7.15)

Решение (7.15) при индуктивности якоря L_Я = const дает закон изменения тока в якоре при неподвижном якоре

(7.16)

где I_к,3 = U/R — ток короткого замыкания двигателя; Т_э == L_я/R—электромагнитная постоянная времени цепи якоря; она имеет размерность времени и определяет ско­рость протекания электромагнитных процессов.

Кривая тока, построенная по (7.16), изображена на рис. 7.6 в пределах промежутка времени t₃ сплошной кри­вой, а за его пределами — штриховой. Время t₃, которое называют временем запаздывания, определяется из (7.16) при подстановке тока i = I_с. В этом случае

t₃ = (7.17)

Следует отметить, что в действительности время запаз­дывания будет несколько больше времени, подсчитанного по (7.17). Это дополнительное запаздывание пуска двига­теля объясняется тормозящим влиянием вихревых токов, возникающих в стали двигателя.

По истечении времениt₃ якорь начнет вращаться. Угло­вая скорость двигателя возрастает, и ЭДС, возникающая в якоре, влияет на ток двигателя. Теперь уже оба процес­са — электромагнитный и электромеханический проте­кают совместно, составляя единый процесс пуска двига­теля. Расчет тока якоря и угловой скорости двигателя при Ф = const необходимо вести, исходя из следующих урав­нений:

U = iR + L_я + e = iR + L_я + сω (7.18)

и

М = М_С + J .

Разделив обе части последнего равенства на с, получим: i = Ic+ . (7.19)

Совместное решение уравнений (7.18) и (7.19) приводит к линейному дифференциальному уравнению второго по­рядка относительноω

(7.20)

где ω_с — установившееся значение угловой скорости при моменте нагрузки М_с.

Решение этого дифференциального уравнения имеет вид:

(7.21)

где α₁, α₂ — корни характеристического уравнения

A,В — постоянные интегрирования, определяющиеся на­чальными условиями.

Соответственно для тока:

(7.22)

При условии, что Т_M > 4 Т_э, корни уравнения α₁ и α₂ имеют действительные отрицательные значения, а выра­жения для угловой скорости и тока с учетом постоянных интегрирования имеют вид:

(7.23)

(7.24)

К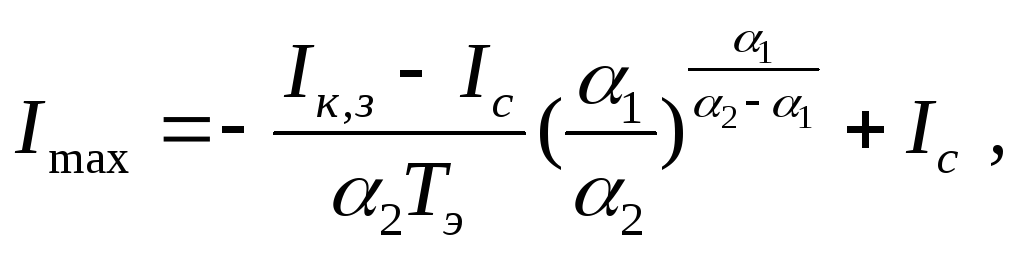ривые угловой скорости и тока, полученные по (7.23) и (7.24), показаны на рис. 7.6. Угловая скорость асимпто­тически стремится кω_с, а ток, достигнув максимума

(7.25)

уменьшается, асимптотически приближаясь к значению Iс. В процессе прямого пуска двигателя индуктивность якоря ограничивает пик тока и увеличивает время пуска. Из (7.25) следует, что максимум тока зависит от соотношения пос­тоянных времени Т_э и Т_М. Реальное соотношение этих постоянных времени таково, что ограничение тока при прямом пуске оказывается незначительным и пик тока превосходит допустимое по условиям коммутации значение. Поэтому прямой пуск (без добавочных резисторов) практиче-

ски недопустим для двигателей мощностью более 0,5—1 кВт. Для ограничения тока при пуске вводится в цепь якоря пусковой резистор. При этом Т_э уменьшается, а Т_M увели­чивается настолько, что оказывается Т_э « Т_M.

Если Т_э « Т_M то можно приближенно принять:

α₁ ≈ — 1/ Т_M и α₂ ≈ —1/ Т_э . (7.26)

Тогда при I_с = 0 получим более простые выражения для определения угловой скорости и тока, а именно:

(7.27)

(7.28)

(7.29)

Как видно из (7.27) — (7.29), при Т_э « Т_M (при боль­шом сопротивлении добавочного резистора) индуктивность якоря практически не сказывается на переходных процес­сах.

Пик тока при прямом пуске можно попытаться умень­шить введением в якорь реактора (индукционной катуш­ки). Однако при этом процесс разбега приобретает неже­лательный колебательный характер, если 4Т_э > Т_м.

При Т_м « 4Т_э корни α₁ и α₂ есть комплексные числа:

α_l,2 = — а ± JΩ,

где а =1/2 Т_э;

Уравнение для определения угловой скорости в данном случае:

(7.30)

здесь

для тока:

(7.31)

Из (7.30) и (7.31) следует, что изменения угловой ско­рости и тока имеют характер затухающих колебаний (рис. 7.7). Из-за колебательного характера процесса су­щественно увеличивается время пуска, возникает значи­тельное перерегулирование угловой скорости (превышение

над установившимся значением) и снижается эффектив­ность ограничения пика тока. Так, для граничного значе­ния Т_э = Т_M /4 при пуске вхолостую I_max ≈ 0,73 I_К,3, а при Т_э = 1,25 Т_м/4 пик тока I_max ≈ 0,52 I_к,з, что обычно превышает допустимый по условиям коммутации ток. Поэ­тому пуск с индукционной катушкой на практике не при­меняют, а используют, пусковые резисторы, при наличии которых влияние индуктивности якоря на процесс, как было показано выше, несущественно.

При торможении или реверсировании влияние электро­магнитных процессов оказывается также незначительным, если в цепь якоря включается дополнительный резистор, сопротивление которого должно быть больше, чем при пуске.

Рис. 7.7. Кривые тока (а) и угло­вой скорости (б) в функции вре­мени при колебательном процессе пуска двигателя постоянного тока независимого возбуждения с доба­вочной индуктивностью в якорной цепи.

Влияние индуктивности якоря на переходный процесс может существенно сказаться при работе двигателя на естественной характеристике в случае резкого приложения или снятия нагрузки как при питании двигателя от сети, так и по системе преобразователь — двигатель. Наличие индуктивности в якорной цепи в переходных режимах нарушает связь между угловой скоростью и моментом, определяемую статической механической характеристи­кой.

В переходных режимах при ударном приложении на­грузки возникает резкое динамическое падение угловой скорости, что отрицательно сказывается на работе многих электроприводов (в металлургии, машиностроении и т. п.). Это динамическое падение угловой скорости должно быть ограничено определенным небольшим значением (около 5—10 % значения установившейся угловой скорости) до приложения нагрузки.

Переходный процесс при ударном приложении нагруз­ки в случае, когда 4T_э > Т_м, протекает так, как показано на рис. 7.8, а—в. До приложения нагрузки двигатель посто­янного тока независимого возбуждения работал на стати­ческой характеристике / с угловой скоростью ω == ω_нач при моменте нагрузки М_С1 (рис. 7.8, в). При скачкообразном

Рис. 7.8. Графики изменения угловой скорости (а), момента (б) и пере­ходного процесса (в) при ударном приложении нагрузки к валу дви­гателя постоянного тока независимого возбуждения, 1 — статическая характеристика; 2 — фазовая траектория.

изменении момента сопротивления до значения Мс2 возни­кает резкое замедление привода, в первый момент равное

и угловая скорость быстро падает (рис. 7.8, а), вызывая вследствие уменьшения ЭДС двигателя рост его тока и мо­мента. Но индуктивность цепи якоря задерживает нараста­ние тока и момента двигателя (рис. 7.8, б), поэтому, когда угловая скорость достигнет значения ω_с , момент двигателя не достигнет значения М_с2, равновесия моментов не будет и угловая скорость будет продолжать снижаться (рис. 7.8, а, б). Лишь после того, как момент двигателя

сравняется со статическим моментом М_с2, уменьшение угловой скорости прекратится. В этой точке угловая ско­рость будет минимальной, а перепад Δω_max — максималь­ным. Это значение перепада угловой скорости и называется динамическим падением угловой скорости, которое обычно больше статического Δω_с .

В точке равенства моментов двигателя и нагрузки угло­вая скорость оказывается меньше, чем это соответствует статической характеристике 1, что влечет за собой (из-за малого значения ЭДС двигателя) дальнейший рост момента до значения М_тах. Угловая скорость возрастает. Когда она достигнет значения ω_с , момент двигателя окажется больше M_С2 и угловая скорость, продолжая расти, превы­шает значение ω_с . Это превышение повлечет за собой умень­шение момента и т. д. Протекающие таким образом коле­бания затухают за счет электрических и механических потерь в системе. После двух-трех колебаний момент и угловая скорость достигнут установившихся значений М_с2 и ω_с .

Отклонение момента и угловой скорости в переходном процессе от значений, соответствующих статической харак­теристике 1, наглядно показывает фазовая траектория про­цесса (кривая 2). Точки этой траектории получают из гра­фиков рис. 7.8, а и б, перенося значения моментов и угло­вой скорости для каждого момента времени в виде одной точки на плоскость ω, М (на рис. 7.8 построение одной точки показано стрелками).

Подобно рассмотренному будет протекать переходный процесс и при резком снятии (сбросе) нагрузки. Колеба­ниями сопровождаются и другие переходные процессы (пуск, торможение, реверс) при отсутствии добавочных резисторов в цепи якоря, когда 4Т_э > Т_м, что часто имеет место, например, в системе управляемый (тиристорный) выпрямитель — двигатель.