Файловый архив студентов. Файловый архив студентов.
1302 вуза, 5124 предмета.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Донецкий национальный технический университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Лин. алгебра и аналит. геометрия / Метод. указания / Варианты инд. задания

.doc
Скачиваний:
25
Добавлен:
03.03.2016
Размер:
805.89 Кб
Скачать
☆

  1. Какому условию должны удовлетворять векторы и , чтобы имело место указанное соотношение.

.

.

при всяких значениях и .

2. Найти вектор , удовлетворяющий указанным условиям.

где

где .

где

3.1 - 18. Выполнить указанные действия над векторами, заданными в различных формах.

3.19 – 25. Найти проекцию вектора на направление вектора .

4. Треугольник ACD задан координатами своих вершин. В каждой задаче, кроме указанного в условии, вычислить площадь треугольника, не находя длины его сторон. Принятые обозначения: точки B, H и M – точки пересечения биссектрис, высот и медиан треугольника соответственно; BA – биссектриса угла при вершине A; HC – высота, опущенная из вершины C на противоположную сторону; MD – медиана проведенная из вершины D. Сделать чертеж.

4.1 A(3;-5), C(-1;-2), D(-3;3). Найти: 1) уравнение и длину BA; 2) уравнение MC;3) угол между BA и HC.

4.2 A(2;8), C(6;4), D(-4;2). Найти: 1) уравнение и длину MA; 2) уравнение HA;3) угол между BA и MA.

4.3 A(0;5), C(-3;4), D(5;0). Найти: 1) уравнение и длину MA; 2) точку H; 3)угол между MA и HA.

4.4 A(-8;2), C(2;2), D(10;8). Найти: 1) уравнение и длину BC; 2) точку H; 3)угол между HD и MC.

4.5 A(-2;-3), C(6;-6), D(2;3). Найти: 1) уравнение и длину HD; 2) точку M; 3) угол между MD и MA.

4.6 A(4;-4), C(0;1), D(-2;4). Найти: 1) уравнение и длину HD; 2) уравнение BA;3) угол между HD и BA.

4.7 A(-3;-8), C(9;0) D(3;8). Найти: 1) уравнение и длину BD; 2) точку M; 3)угол между BD и MD.

4.8 A(0;10), C(4;6) D(-6;4). Найти: 1) уравнение и длину MD; 2) центр описанной окружности и ее радиус; 3) углы треугольника.

4.9 A(1;7), C(-2;-2) D(6;2). Найти: 1) уравнение AK║CD; 2) точку H; 3) угол между HC и MA.

4.10 A(8;6), C(2;0) D(6;8). Найти: 1) уравнение и длину HC; 2) уравнение KL, где K и L – середины сторон CD и CA; 3) угол ACM.

4.11 A(8;14), C(16;-2) D(2;-4). Найти: 1) уравнение и длину MD; 2) центр описанной окружности и ее радиус; 3) угол между HA и MD.

4.12 A(4;2), C(6;-12) D(18;0). Найти: 1) уравнение и длину MA; 2) центр вписанной окружности и ее радиус; 3) угол CBA.

4.13 A(-7;-3), C(1;9) D(9;3). Найти: 1) уравнение и длину HC; 2) точку M; 3)угол между HC и MA.

4.14 A(-5;-1), C(5;-1) D(13;5). Найти: 1) уравнение и длину MС; 2) точку H; 3) угол между BC и HD.

4.15 A(1;-2), C(-2;0) D(5;6). Найти: 1) уравнение и длину BA; 2) центр описанной окружности и ее радиус; 3) уравнение HA.

4.16 A(2;14), C(-4;-4) D(12;4). Найти: 1) уравнение и длину PQ, где P и Q – середины сторон AC и AD; 2) точку H; 3) угол между MA и HA.

4.17 A(-6;-13), C(12;-7) D(4;17). Найти: 1)уравнение и длину HC; 2)точку B; 3) угол между MC и HC.

4.18 A(2;-8), C(2;2) D(8;10). Найти: 1) уравнение и длину HC; 2) центр описанной окружности и ее радиус; 3) угол DMC.

4.19 A(0;-1), C(4;5) D(8;-4). Найти: 1) уравнение DK║AC; 2) точку M; 3)угол между HD и MD.

4.20 A(0;4), C(2;-10) D(14;2). Найти: 1) уравнение CD; 2) центр вписанной окружности и ее радиус; 3) угол между HC и MA.

4.21 A(4;5), C(-3;-1) D(0;-3). Найти: 1) уравнение и длину BD; 2) уравнение AK║CD; 3) углы треугольника.

4.22 A(3;0), C(-3;2), D(3;8). Найти: 1) уравнение и длину HA; 2) центр описанной окружности и ее радиус; 3) угол между HA и MC.

4.23 A(-2;1), C(6;-5) D(-2;11). Найти: 1) уравнение и длину BA; 2) точку H; 3) угол MAC.

4.24 A(2;4), C(-12;6) D(0;18). Найти: 1) уравнение и длину HA; 2) точку B; 3) расстояние от B до стороны AD.

4.25 A(2;-6), C(-2;-3) D(-4;2). Найти: 1) уравнение и длину MC; 2)уравнение HD;3)угол между HD и MC.

5.Установить, какую линию определяет уравнение, определить фокусы, вершины, оси линии, нарисовать ее.

5.1. 4x2 – y2 –8x – 4y – 4 = 0.

    1. x2 + y2 –2x – 4y + 1 = 0.

    2. 4y2 – 8x – 4y + 9 = 0.

    3. x2 – 4y2 + 8y + 4 = 0.

    4. x2 + 2x + 4y – 7 = 0.

    5. 4x2 + 4y2 – 8x – 24y + 31 = 0.

    6. x2 + 4y2 + 4x – 8y + 4 = 0.

    7. x2 – y2 – 6x – 4y + 1 = 0.

    8. y2 + 8x – 6y + 25 = 0.

    9. x2 + y2 + 8x + 2y + 1 = 0.

    10. 4x2 + y2 – 8x + 4y + 4 = 0.

    11. 4x2 – y2 – 8x – 6y – 9 = 0.

    12. y2- 16x + 6y + 25 = 0.

    13. 2x2 + 2y2 + 16x – 28y + 53 = 0.

    14. x2 + 9y2 –2x +18y + 1 = 0.

    15. x2 – 4y2 – 8x +8y + 16 = 0.

    16. x2 – 4x – 4y + 12 = 0.

    17. x2 + y2 – 8x + 2y + 16 = 0.

    18. 9x2 + 4y2 – 18x + 24y + 9 = 0.

    19. x2 – 9y2 – 8x + 18y – 2 = 0.

    20. 3x2 + 3y2 – 42x + 6y + 146 = 0.

    21. y2 + 10x – 10y + 55 = 0.

    22. 9x2 – 16y2 – 36x + 32y + 164 = 0.

    23. y2 – 20x – 14y + 37 = 0.

    24. 9x2 + 16y2 – 18x + 96y + 9 = 0.

6.Установить , какая линия определяется уравнением , нарисовать ее.

6.1. 6.2.

6.3. 6.4.

6.5. 6.6.

6.7. 6.8.

6.9. 6.10.

6.11. 6.12.

6.13. 6.14.

6.15. 6.16.

6.17. 6.18.

6.19. 6.20.

6.21. 6.22.

6.23. 6.24.

6.25.

7.1-8.Провести касательные к линии l , параллельные прямой p.

7.1. l: , p: 2x+y-7=0.

7.2. l: , p: 4x-2y+23=0.

7.3. l: , p: 10x-3y+9=0.

7.4. l: , p: 3x-2y+13=0.

7.5. l: , p: 3x-4y+7=0.

7.6. l: , p: 2x+2y-13=0.

7.7. l: , p: x-y-7=0.

7.8. l: , p: 2x-y+3=0.

7.9-16.Провести касательные к линии l , перпендикулярные прямой p.

7.9. l: , p: x-2y+9=0.

7.10. l: , p: 2x-2y-5=0.

7.11. l: , p: 4x+3y-7=0.

7.12. l: , p: 4x+2y-1=0.

7.13. l: , p: y-2x-4=0.

7.14. l: , p: 3x-2y-6=0.

7.15. l: , p: 5x+2y+8=0.

7.16. l: , p: x+y-17=0.

7.17-21.Через точку М провести касательную к линии l .

7.17. M(-9;3), l: .

7.18. M( 2;2), l: .

7.19. M(0;-6), l: .

7.20. M(0;11), l: .

7.21. M( 7;0), l: .

7.22-25.Вывести условие, при котором прямая y=kx+b касается линии l .

7.22. l : .

7.23. l : .

7.24. l : .

7.25. l : .

8. Определить параметры, входящие в уравнения прямых и плоскостей, используя данные об их взаимном расположении.

8.1

8.2

8.3

8.4

8.5

8.6

8.7

8.8

8.9

8.10

8.11

8.12 )

8.13

8.14

8.15

8.16

8.17

    4. - пересекаются

    5. p и q – пересекаются

    6. p и q – пересекаются

9. Составить уравнение плоскости и найти расстояние точки N от неё. Выяснить, лежат ли точка N и начало координат по одну или по разные стороны относительно плоскости .

9.1 А.

9.2 .

9.3 .

9.4 линии пересечения плоскостей

.

9.5 .

9.6 .

9.7 .

9.8 .

9.9 .

9.10 проходит через линию пересечения плоскостей

.

9.11 .

9.12

.

9.13 .

9.14 .

9.15 .

9.16 .

9.17 .

9.18 .

9.19 .

9.20 .

9.21 .

9.22 .

9.23 .

9.24 .

9.25

10.Составить канонические, параметрические или общие уравнения прямой р,проходящей через точку N, используя данные о расположении p относительно других объектов.

    1. N (-1,2,-3) , p|| q:.

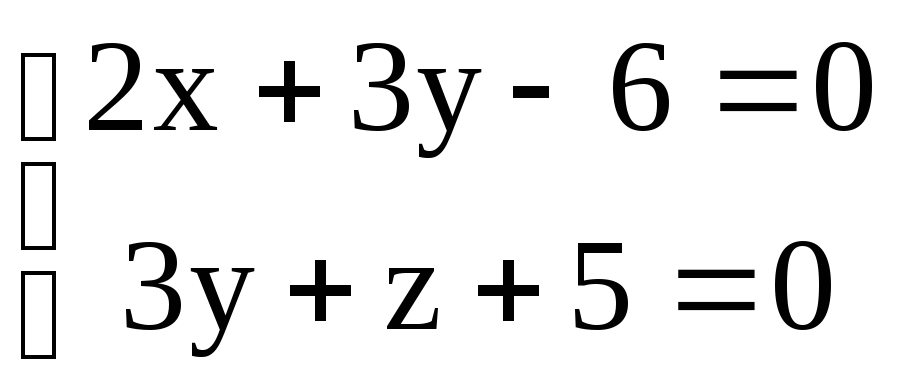    2. N (2,2,5) , p ={1,2,0}, ={0,3,7}.

    3. N (1,0,5) , p||: 3x-y+7z=0 , p пересекается с прямой

Соседние файлы в папке Метод. указания
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности