§6. Другие виды уравнения плоскости

I Уравнение плоскости, проходящей через три точки

Выведем уравнение плоскости, которая проходит через три различные точки M₁(x₁,y₁,z₁), M₂(x₂,y₂,z₂) и M₃(x₃,y₃,z₃), не лежащие на одной прямой. Так как указанные точки не лежат на одной прямой, векторы инеколлинеарны, а потому произвольная точкаM(x,y,z) лежит в одной плоскости с точками M₁, M₂, M₃ тогда и только тогда, когда векторы ,икомпланарны. Но компланарность равносильна равенству нулю смешанного произведения векторов. Записав смешанное произведение через проекции векторов, получим:

. (1)

Это и есть уравнение плоскости проходящей через данные три точки.

II Уравнение плоскости “в отрезках”

Рассмотрим плоскость, которая пересекает все координатные оси и не проходит через начало координат. Введем обозначения для точек пересечения с осями: M₁(a;0;0), M₂(0;b;0) и M₃(0;0;c). Составим уравнение плоскости, используя формулу (1):

.

Вычислив определитель, получим:

(x–a)bc+yac+zab=0.

Разделим обе части уравнения на abc:

.

И окончательно

. (2)

Это и есть уравнение плоскости “в отрезках”.

§7. Прямая в пространстве

I Общие уравнения прямой

Как уже говорилось ранее, в аналитической геометрии линию в пространстве понимают как пересечение двух поверхностей. В частности, прямую линию мы будем рассматривать как пересечение двух плоскостей. Поэтому, если в пространстве задананекоторая ДПСК,то уравнениями прямойслужит система двух уравнений первой степени:

(1)

Будем называть эти уравнения общими уравнениями прямой (конечно, предполагается, что прямые пересекаются).

Очевидно, существует бесчисленное множество пар плоскостей, пересекающихся по данной прямой, и соответственно этому существует бесчисленное множество общих уравнений (1) для данной прямой.

Общие уравнения удобны при решении задачи о пересечении прямой и плоскости или двух прямых, задачи о проектировании прямой на плоскость. В других задачах более удобными оказываются иные формы уравнений прямой.

II Канонические уравнения прямой

Определение. Всякий ненулевой вектор, лежащий на данной прямой или параллельный ей, называется ее направляющим вектором. Обозначение: .

Составим уравнение прямой, проходящей через точку M₀(x₀,y₀,z₀) в направлении вектора . Возьмем текущую точку прямойM(x,y,z) и рассмотрим вектор . Он лежит на данной прямой и поэтому коллинеарен ее направляющему вектору. Осталось написать условие коллинеарности, т.е. пропорциональность проекций:

. (2)

Это и есть канонические уравнения прямой, проходящей через точку M₀(x₀,y₀,z₀) и имеющей направляющий вектор .

Пример. Найти канонические уравнения прямой

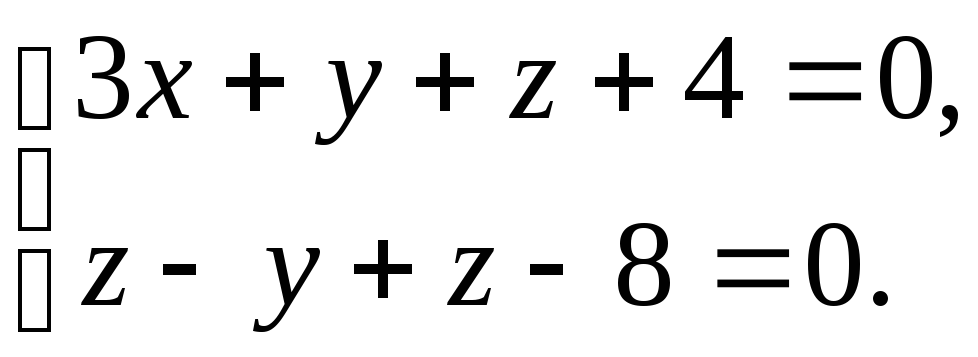(3)

Решение. Чтобы составить канонические уравнения прямой, нужно: 1) найти какую-либо точку прямой; 2) найти направляющий вектор прямой.

1) Найти какую-нибудь точку прямой (3) – это означает найти какое-нибудь решение этой системы двух уравнений с тремя неизвестными. Положим, например, x=0. Система (3) превратится в

Отсюда нетрудно найти: z=2, y= –6. Итак, точка M₀(0;–6; 2) принадлежит прямой (3).

2) Прямая определена как пересечения двух плоскостей, значит она лежит в каждой из них и поэтому перпендикулярна их нормальным векторам и. В качестве направляющего вектора можно взять любой вектор перпендикулярный к векторами, например, их векторное произведение

,

или вектор, коллинеарный ему . Итак, искомые канонические уравнения имеют вид

Пример. Составить уравнения прямой, проходящей через точки M₁(x₁,y₁,z₁) и M₂(x₂,y₂,z₂).

Решение. Для того, чтобы использовать канонические уравнения (2), положим M₀=M₁, . Получим:

. (4)

Имея эти уравнения, предыдущей пример можно решить, не находя направляющий вектор прямой. Надо только найти не одну точку, лежащую на прямой, а две.