Тема Плоскость и прямая в пространстве.

§1. Уравнение поверхности и уравнения линии

I Поверхность

Соотношение вида F(x,y,z)=0, где F(x,y,z) – выражение с переменными, называется уравнением с тремя переменными. Например, x+2y+3z–1=0, x²+y²–25=0, x–1=0.

Говорят, что три числа x=x₀, y=y₀, z=z₀ удовлетворяют данному уравнению с тремя переменными, если при подстановке их в это уравнение вместо переменных оно становится верным числовым равенством.

Пусть теперь в пространстве задана некоторая поверхность и выбрана некоторая ДПСК. Тройку чисел (x,y,z) понимаем как координаты точки пространства.

Определение 1. Уравнением данной поверхности называют такое уравнение с тремя переменными, которому удовлетворяют координаты каждой точки, лежащей на этой поверхности, и не удовлетворяют координаты ни одной точки, не лежащей на ней.

Определение 2. Поверхность, определяемая данным уравнением вида F(x,y,z)=0, есть множество всех точек пространства, координаты которых удовлетворяют этому уравнению.

С этими определениями связны две задачи аналитической геометрии в пространстве: 1) по словесному определению поверхности, по свойствам ее точек составить уравнение поверхности; 2) зная уравнения поверхности, выяснить свойства ее точек, изобразить поверхность.

Замечание. Задание поверхности уравнением F(x,y,z)=0 называется неявным. Если же это уравнение удается разрешить относительно одной из переменных и получить, например, z=f(x,y), то говорят о явном задании поверхности. Отметим, что существует и параметрический способ задания поверхности, но его мы будем рассматривать позже.

II Линия в пространстве

Линию в пространстве естественно рассматривать как пересечение двух поверхностей.

Именно, если F(x,y,z)=0 и Ф(x,y,z)=0 есть уравнения двух поверхностей, пересекающихся по некоторой линии L, то линия L есть множество общих точек этих поверхностей, т.е. множество точек, координаты которых удовлетворяют одновременно обоим уравнениям.

Таким образом, система двух уравнений

(1)

определяет линию L, т.е. является уравнениями этой линии.

Например, уравнения

двух плоскостей определяют прямую, проходящую через начало координат и точку P(1;1;2) (координаты точек О и Р удовлетворяют обоим уравнениям).

Однако, задание линии уравнениями (1) не всегда удобно. Возможен, и очень естественен с кинематической точки зрения, другой подход к понятию линии: линия – это траектория движения материальной точки. Этот подход приводит к параметрическим уравнениям линии, когда абсцисса, ордината и аппликата текущей точки линии выражаются функциями вспомогательной переменной – параметра t:

Например, параметрические уравнения

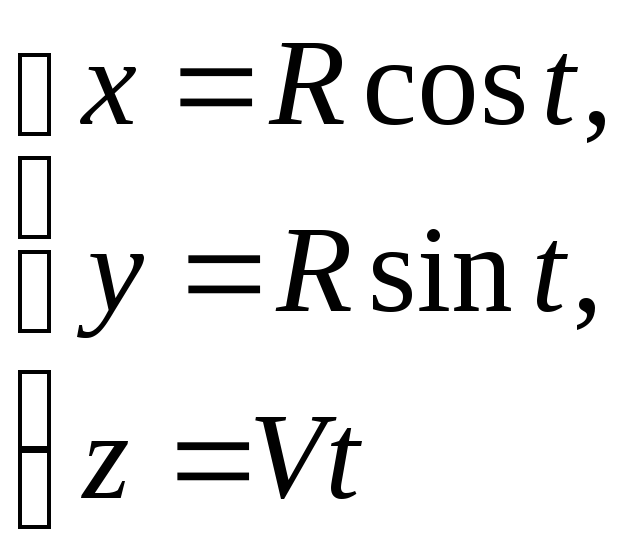
задают так называемую винтовую линию. Ее можно понимать как траекторию точки, движущейся равномерно по образующей кругового цилиндра, если сама образующая равномерно вращается вокруг оси цилиндра.

§2. Общее уравнение плоскости

Будем считать, что в пространстве задана некоторая ДПСК.

Определение. Всякий ненулевой вектор, перпендикулярный данной плоскости, называется ее нормальным вектором. Обозначение:

Теорема. В декартовых координатах всякая плоскость определяется уравнением первой степени, т.е. уравнением вида

Ax+By+Cz+D=0. (1)

И обратно: всякое уравнение вида (1) определяет в пространстве некоторую плоскость.

Доказательство этой теоремы аналогично доказательству теоремы об общем уравнении прямой на плоскости.

Уравнение (1) называют общим уравнением плоскости. Коэффициенты A,B,C – это проекции нормального вектора плоскости.

Уравнение вида

A(x–x₀)+B(y–y₀)+C(z–z₀)=0

является уравнением плоскости, проходящей через точку M₀(x₀;y₀;z₀) и имеющей нормальный вектор

Пример. Составить уравнение плоскости α, проходящей через данную точку M₀(1;2;3) и перпендикулярной плоскостям β:x+2y–z=0 и γ:2x–y+3z+1=0.

Решение. Нормальные векторы иплоскостейβ и γ перпендикулярны своим плоскостям, а значит параллельны плоскости α, т.к. и. Но тогда векторное произведение, будучи перпендикулярным своим сомножителям, будет также перпендикулярным к плоскости, т.е. оно является нормальным вектором этой плоскости. Найдем его:

Вектор , коллинеарный, также будет нормальным вектором искомой плоскостиα. Теперь можем составить ее уравнение:

1(x–1)+(–1)(y–2)+(–1)(x–3)=0 или

x–y–z+4=0.