§2. Елементарні функції

I Основні елементарні функції

До основних елементарних функцій відносять константи, степеневі, показникові, логарифмічні, тригонометричні й обернені тригонометричні.

1) Константа y = Const.

D(y) = R, E(y)={c}.

не існує, парна.

Графік – пряма, паралельна осі абсцис.

2) Степенева.

D(y) і E(y) залежать від , але 

(0, +) D(y).

Парність-непарність залежить від

показника .

Обернена для є .

Для <0 осі координат –

асимптоти.

3) Показникова (0<a1).

D(y) = R, E(y) = (0, +).

Функція загального виду.

Вісь абсцис – асимптота.

Обернена для функції є

логарифмічна функція

4)Логарифмічна (0<a1).

D(y) = (0, +), E(y) = R.

Функція загального виду.

Вісь ординат – асимптота.

Обернена для логарифмічної –показникова функція.

У математичному аналізі в основному використовують натуральні логарифми lnx, тобто логарифми з основою a=e=2,7…

5)Тригонометричні

а) .

D(y) = R, E(y) = [1, 1].

Непарна.

Періодична, .

б) .

D(y) = R, E(y) = [1, 1].

Парна.

Періодична, .

в) .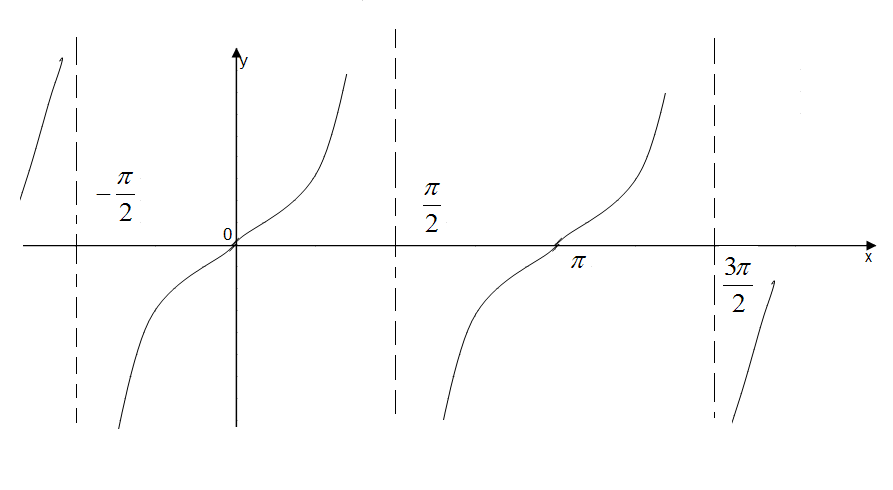

D(y) = R \ {,kz},

E(y) = R.

Непарна.

Періодична, .

Прямі  асимптоти.

г) .

D(y) = R \{k, kz}, E(y) = R

Непарна.

Періодична, .

Прямі x = k  асимптоти.

6) Обернені тригонометричні

При визначенні цих функцій вибираються наступні проміжки монотонності: для синуса  , для косинуса [0, ], для тангенса , для котангенса (0, ).

Визначення, наприклад, арксинуса: arcsina – це кут   такий, що sin=a. Інші функції визначаються аналогічно.

а) .

D(y) = [1, 1], E(y) = .

Непарна.

б) .

D(y) = [1, 1], E(y) = [0, ].

arccos(x) =   arccosx.

arcsinx + arccosx = .

в) .

D(y) = R, E(y) = .

Непарна.

Прямі  асимптоти.

г) .

D(y) = R, E(y) = (0, ).

arcctg(x) =   arcctgx.

Прямі y = 0 і y =   асимптоти.

Зауваження. Іноді до основних елементарних функцій відносять ще й т.зв. гіперболічні функції й обернені до них. Всі ці функції досить просто виражаються через показникову й логарифмічну функції.

а) синус гіперболічний : D(y) = R, E(y) = R, непарна; обернена функція має вигляд y = Arshx = .

б) косинус гіперболічний : D(y) = R, E(y) = [1, +), парна; обернена функція має вигляд y = Archx = , (у функції chx береться проміжок ).

в) тангенс і котангенс гіперболічні визначаються так само, як і в тригонометрії:

, .

Обернена функція для y = thx – це y = Arthx = . Графіки гіперболічних функцій:

II Елементарні функції

Означення. Елементарною називають функцію, що може бути задана явно однією формулою, що містить скінчене число арифметичних операцій і суперпозицій, застосованих до основних елементарних функцій.

Слід зазначити, що деякі функції, задані декількома формулами (тобто, загалом кажучи, неелементарні), іноді вдається записати однією формулою. Прикладом служить функція y = |x|. За означенням

У той же час маємо: . Таким чином, функціяy = |x|  елемен-тарна. Її графік: