
- •104 Тема дослідження функцій за допомогою похідних
- •§1. Умова сталості функції
- •§2. Умова монотонності функції
- •§3. Дослідження функції на екстремум
- •§4. Дослідження функції на опуклість і перегин
- •I Напрямок опуклості (увігнутості)
- •II Точки перегину
- •§5. Асимптоты графіка функції
- •I Вертикальні асимптоти
- •II Горизонтальні асимптоти
- •III Похилі асимптоти
- •§6. Загальна схема дослідження функції
- •§7. Найбільше й найменше значення функції на проміжку
- •Тема формули тейлора й маклорена
- •§1. Формула Тейлора для многочлена. Біном Ньютона
- •§2. Формула Тейлора для довільної функції
- •I Означення
- •II Формула Тейлора із залишковим членом у формі Пеано
- •III Формула Тейлора із залишковим членом у формі Лагранжа
- •§3. Формула Маклорена. Оцінка Rn(X)
- •I Формула Маклорена
- •II Універсальна оцінка залишкового члена
- •§4. Розкладання по формулі Маклорена деяких елементарних функцій
- •§5. Застосування формули Маклорена
- •I Обчислення границь
- •II Наближені обчислення
- •Iiі Дослідження функцій
Тема формули тейлора й маклорена
Лекція 15
§1. Формула Тейлора для многочлена. Біном Ньютона
Нагадаємо формулу для обчислення похідних (будь-якого порядку) степеневої функції з натуральним показником степені:
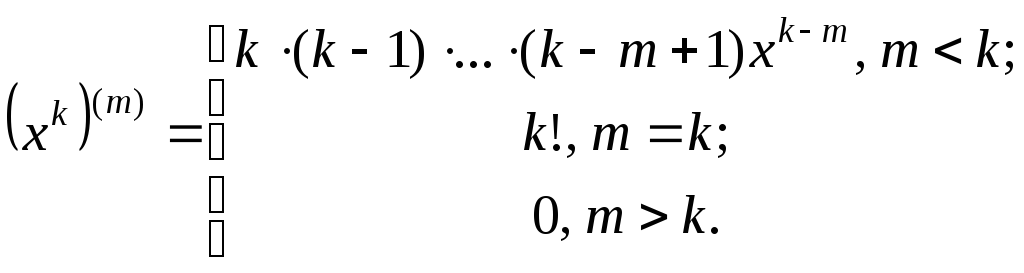
За допомогою цієї формули встановимо зв'язок між коефіцієнтами многочлена
![]() (1)
(1)
і похідними самого многочлена в нулі. Запишемо многочлена у вигляді
![]()
Перший
доданок правої частини після k-кратного
диференціювання обернеться в нуль, а
другий
– в
![]() Длятретього
маємо:
Длятретього
маємо:

У цій
сумі всі показники степені
![]() .
Щоб ця сума звернулася в нуль, досить
покласти
.
Щоб ця сума звернулася в нуль, досить
покласти
![]() Отже, одержимо
зв'язок:
Отже, одержимо
зв'язок:
![]() Звідси
випливає формула, що виражає коефіцієнти
многочлена через похідні самого
многочлена:
Звідси
випливає формула, що виражає коефіцієнти
многочлена через похідні самого
многочлена:
![]() (2)
(2)
Тепер многочлен (1) можна записати у формі
![]()
Нагадаємо, що похідна нульового порядку – це сама функція.
Іноді
потрібно многочлен (1) записати не по
степенях
![]() ,
а по степенях двочлена
,
а по степенях двочлена![]() Неважко переконатися, що в цьому випадку
коефіцієнти обчислюються по формулі
Неважко переконатися, що в цьому випадку
коефіцієнти обчислюються по формулі![]() а сам многочлен можна записати у вигляді
а сам многочлен можна записати у вигляді
![]()
Це і є формула Тейлора для многочлена.
З формули (2) для коефіцієнтів многочлена (1) можна вивести два важливих наслідки.
Наслідок 1. Розглянемо два многочлени
![]() і
і
![]()
Якщо
![]() то й
то й![]() звідкиодержимо:
а) степені
многочленів рівні
–
звідкиодержимо:
а) степені
многочленів рівні
–
![]() ;
б) коефіцієнти при однакових степеняхзмінної
рівні
–
;
б) коефіцієнти при однакових степеняхзмінної
рівні
–
![]()
Наслідок
2.
Розглянемо
многочлен, що представляє
собою
![]() степінь бінома
степінь бінома![]() й запишемойого
в стандартній формі (1):
й запишемойого
в стандартній формі (1):
![]() .
.
Коефіцієнти обчислимо по формулі (2):

Отже, ми одержали т.зв. формулу бінома Ньютона:
![]()
Числа
![]() позначають
позначають
![]() і
називають біноміальними коефіцієнтами.
Тому що
і
називають біноміальними коефіцієнтами.
Тому що
![]() ,
можна використовувати
компактний запис цих чисел:
,
можна використовувати
компактний запис цих чисел:
![]()
Ці числа
виникають у задачах
комбінаторики, де вони називаються
«числом сполучень із
![]() по
по![]() »
і дають відповідь на питання: «Скількома
способами можна вибрати
»
і дають відповідь на питання: «Скількома
способами можна вибрати![]() предметів із
предметів із![]() предметів, якщо не важливий порядок
вибору?»
предметів, якщо не важливий порядок
вибору?»
Приклад.
Запишемо многочлен
![]() по степенях
по степенях![]() .
Відповідно до формулиТейлора
маємо:
.
Відповідно до формулиТейлора
маємо:
![]()
Тут:
![]()
![]()
![]()
![]()
Отже,
![]()
§2. Формула Тейлора для довільної функції
I Означення
Розглянемо
функцію
![]() ,
що має вточці
,
що має вточці
![]() похідні всіх порядків доп-го
включно. Складемо для цієї функції
многочлен
похідні всіх порядків доп-го
включно. Складемо для цієї функції
многочлен
![]()
![]() .(1)
.(1)
З
результатів попереднього параграфа :
коефіцієнт при
![]() ,
тобто
,
тобто
![]() ,
повинен рівнятися
,
повинен рівнятися
![]() .
Таким чином, многочлен (1) задовольняє
співвідношенням:
.
Таким чином, многочлен (1) задовольняє
співвідношенням:
![]()
![]()
Оскільки
функція
![]() не многочлен, то вже не можна очікувати
рівності
не многочлен, то вже не можна очікувати
рівності![]() .
Однак, через збіг похідних природно
очікувати, що
.
Однак, через збіг похідних природно
очікувати, що![]() .
Тому особливий інтересздобуває
вивчення різниці
.
Тому особливий інтересздобуває
вивчення різниці
![]()
Для похідних цієї функції справедливі співвідношення:
![]()
![]() (2)
(2)
Для
останнього,
мабуть, потрібно, щоб у
функції
![]() існувала похідна
існувала похідна![]() -го
порядку.
-го
порядку.
Прийнято наступну термінологію:
1)
многочлен (1):
![]() – многочленТейлора
порядку
– многочленТейлора
порядку
![]() для функції
для функції![]() ;
;
2)
формула
![]() – формула Тейлора
порядку
– формула Тейлора
порядку
![]() для функції
для функції![]() або розкладання по формуліТейлора
функції
або розкладання по формуліТейлора
функції
![]() ;
;
3)
різниця
![]() – залишковий член формулиТейлора.
Для різних цілей є різні форми залишкового
члена. Формули Тейлора
й розрізняють по цих формах. Ми розглянемо
лише 2 форми залишкового члена.
– залишковий член формулиТейлора.
Для різних цілей є різні форми залишкового
члена. Формули Тейлора
й розрізняють по цих формах. Ми розглянемо
лише 2 форми залишкового члена.
