Приклади розв'язання задач

Задача 14.1.

Структурна схема нелінійної автоматичної системи зображена на рис.14.2,а. Коефіцієнт передачі лінійної частини системи й нелінійної ланки умовно віднесений до нелінійної ланки. Визначити, при яких значенняхсистема буде абсолютно стійка, якщо характеристика нелінійної ланки розташована в сектори (0,) (рис. 14.2,б). Вихідні дані: постійна часу лінійної частини системи,,.

Рисунок 14.2.  Структурна схема системи й статична характеристика нелінійної ланки.

Рішення.

Частотна передаточна функція лінійної частини системи має вигляд

. (14.1)

Її дійсна й мнима частини відповідно рівні

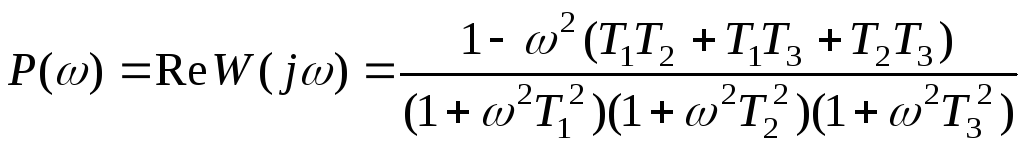, (14.2)

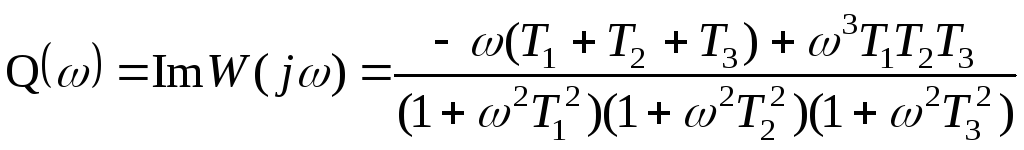. (14.3)

Введемо деякі функції йу такий спосіб:

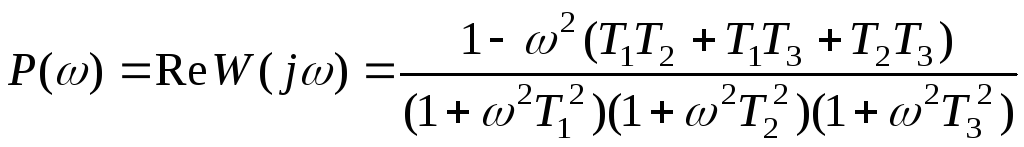, (14.4)

(14.5)

По вираженнях (14.5) і (14.5) побудуємо характеристику й через точку () проведемо пряму Попова так, щоб побудована характеристика цілком лежала праворуч від цієї прямої (рис.14.3.)

jQ*()

P*()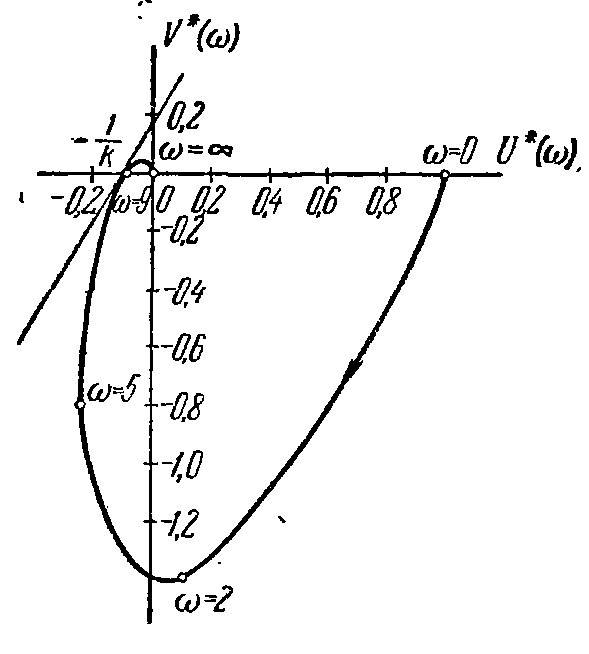

Рисунок 14.3. Модифікована АФЧХ до задачі 14.1.

Згідно рис.14.3. . Тому система абсолютно стійка для всіх нелінійних характеристик розташованих у секторі

(14.6)

і, зокрема, для характеристики релейного типу, зображеної на рис.14.2,б.

Таким чином, достатня умова абсолютної стійкості замкнутої нелінійної системи зводиться в цьому випадку до виконання необхідної й достатньої умови стійкості замкнутої лінійної системи, що має в розімкнутому стані коефіцієнт передачі, рівний .

Задача 14.2.

Структурна схема нелінійної автоматичної системи зображена на рис.14.4,а. Перевірити виконання достатньої умови абсолютної стійкості системи при наступних значеннях параметрів системи: ,,,, коефіцієнт передачі лінійної частини системи, коефіцієнт підсилення нелінійної ланки(рис.14.4,б).

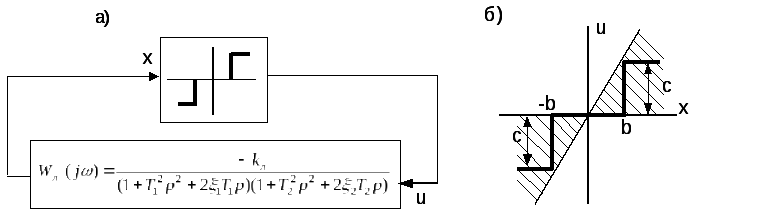
Рисунок 14.4. Структурна схема системи й характеристика нелінійної ланки.

Рішення.

Коефіцієнт передачі розімкнутої системи

віднесемо до нелінійної ланки. Тоді частотна передаточна функція розімкнутої системи буде дорівнює

(14.7)

Визначаємо функції

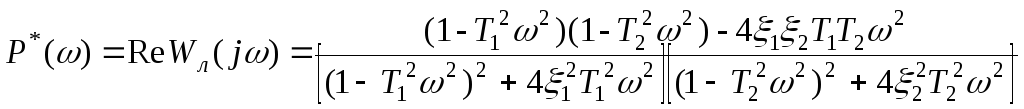, (14.8)

. (14.9)

По вираження (14.8) і (14.9) будуємо характеристику (рис.14.5) на речовинній осі відкладемо точку з координатами. Через цю точку можна провести пряму Попова так, що вся побудована характеристика буде розташовуватися праворуч від неї. Отже, дана система буде стійкою при заданому, якщо статична характеристика нелінійної ланки цілком розташовується в секторі. Цей сектор заштрихований на рис.14.4,б.

jQ*()

P*()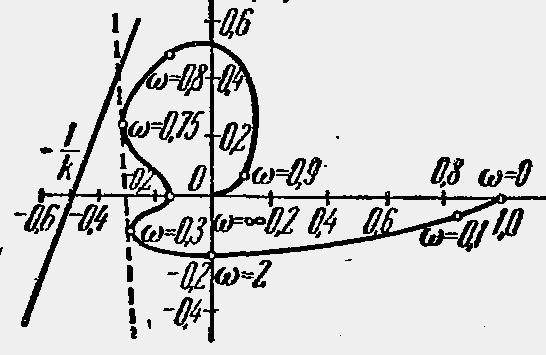

Рисунок 14.5. Модифікована АФЧХ до задачі 14.2.

СПИСОК ЛИТЕРАТУРЫ

1. Воронов А.А. Основы теории автоматического управления. Автоматическое регулирование непрерывных линейных систем.– М.:Энергия, 1980.- 310с.

2. Теория автоматического управления. Ч. 1/ под общей редакцией Нетушила А.В. – М.: Высшая школа, 1968.- 424с.

3. Лукас В. А. Теория автоматического управления. – М.: Недра, 1990. – 416 с.

4. Попов Е.П. Теория нелинейных систем автоматического регулирования и управления. М.: Наука, 1989. 304 с.

5. Расчет автоматических систем / под редакцией Фатеева А.В.– М.: Высшая школа, 1973.- 336с.

6.Сборник задач по теории автоматического регулирования и управления/под редакцией Бесекерского В.А. – М.:Наука,1978.-510с.

Навчальне видання

Методичні вказівки до проведення практичних занять з курсу

"Теорія автоматичного управління"

Частина 2

Для студентів, що навчаються за напрямами