
Для студентов ЭКИ-1 / RGR-1
.doc4.11 A(8;14), C(16;-2) D(2;-4). Найти: 1) уравнение и длину MD; 2) центр описанной окружности и ее радиус; 3) угол между HA и MD.
4.12 A(4;2), C(6;-12) D(18;0). Найти: 1) уравнение и длину MA; 2) центр вписанной окружности и ее радиус; 3) угол CBA.
4.13 A(-7;-3), C(1;9) D(9;3). Найти: 1) уравнение и длину HC; 2) точку M; 3)угол между HC и MA.
4.14 A(-5;-1), C(5;-1) D(13;5). Найти: 1) уравнение и длину MС; 2) точку H; 3) угол между BC и HD.
4.15 A(1;-2), C(-2;0) D(5;6). Найти: 1) уравнение и длину BA; 2) центр описанной окружности и ее радиус; 3) уравнение HA.
4.16 A(2;14), C(-4;-4) D(12;4). Найти: 1) уравнение и длину PQ, где P и Q – середины сторон AC и AD; 2) точку H; 3) угол между MA и HA.
4.17 A(-6;-13), C(12;-7) D(4;17). Найти: 1)уравнение и длину HC; 2)точку B; 3) угол между MC и HC.
4.18 A(2;-8), C(2;2) D(8;10). Найти: 1) уравнение и длину HC; 2) центр описанной окружности и ее радиус; 3) угол DMC.
4.19 A(0;-1), C(4;5) D(8;-4). Найти: 1) уравнение DK║AC; 2) точку M; 3)угол между HD и MD.
4.20 A(0;4), C(2;-10) D(14;2). Найти: 1) уравнение CD; 2) центр вписанной окружности и ее радиус; 3) угол между HC и MA.
4.21 A(4;5), C(-3;-1) D(0;-3). Найти: 1) уравнение и длину BD; 2) уравнение AK║CD; 3) углы треугольника.
4.22 A(3;0), C(-3;2), D(3;8). Найти: 1) уравнение и длину HA; 2) центр описанной окружности и ее радиус; 3) угол между HA и MC.
4.23 A(-2;1), C(6;-5) D(-2;11). Найти: 1) уравнение и длину BA; 2) точку H; 3) угол MAC.
4.24 A(2;4), C(-12;6) D(0;18). Найти: 1) уравнение и длину HA; 2) точку B; 3) расстояние от B до стороны AD.
4.25 A(2;-6), C(-2;-3) D(-4;2). Найти: 1) уравнение и длину MC; 2)уравнение HD;3)угол между HD и MC.
5.Установить, какую линию определяет уравнение, определить фокусы, вершины, оси линии, нарисовать ее.
5.1. 4x2 – y2 –8x – 4y – 4 = 0.
-
x2 + y2 –2x – 4y + 1 = 0.
-
4y2 – 8x – 4y + 9 = 0.
-
x2 – 4y2 + 8y + 4 = 0.
-
x2 + 2x + 4y – 7 = 0.
-
4x2 + 4y2 – 8x – 24y + 31 = 0.
-
x2 + 4y2 + 4x – 8y + 4 = 0.
-
x2 – y2 – 6x – 4y + 1 = 0.
-
y2 + 8x – 6y + 25 = 0.
-
x2 + y2 + 8x + 2y + 1 = 0.
-
4x2 + y2 – 8x + 4y + 4 = 0.
-
4x2 – y2 – 8x – 6y – 9 = 0.
-
y2- 16x + 6y + 25 = 0.
-
2x2 + 2y2 + 16x – 28y + 53 = 0.
-
x2 + 9y2 –2x +18y + 1 = 0.
-
x2 – 4y2 – 8x +8y + 16 = 0.
-
x2 – 4x – 4y + 12 = 0.
-
x2 + y2 – 8x + 2y + 16 = 0.
-
9x2 + 4y2 – 18x + 24y + 9 = 0.
-
x2 – 9y2 – 8x + 18y – 2 = 0.
-
3x2 + 3y2 – 42x + 6y + 146 = 0.
-
y2 + 10x – 10y + 55 = 0.
-
9x2 – 16y2 – 36x + 32y + 164 = 0.
-
y2 – 20x – 14y + 37 = 0.
-
9x2 + 16y2 – 18x + 96y + 9 = 0.
6.Установить , какая линия определяется уравнением , нарисовать ее.
6.1. ![]() 6.2.
6.2. ![]()
6.3. ![]() 6.4.
6.4. ![]()
6.5. ![]() 6.6.
6.6. ![]()
6.7. ![]() 6.8.
6.8. ![]()
6.9. ![]() 6.10.
6.10. ![]()
6.11. ![]() 6.12.
6.12. ![]()
6.13. ![]() 6.14.
6.14. ![]()
6.15. ![]() 6.16.
6.16. ![]()
6.17. ![]() 6.18.
6.18. ![]()
6.19. ![]() 6.20.
6.20. ![]()
6.21. ![]() 6.22.
6.22. ![]()
6.23. ![]() 6.24.
6.24.![]()
6.25. ![]()
7.1-8.Провести касательные к линии l , параллельные прямой p.
7.1. l: ![]() , p: 2x+y-7=0.
, p: 2x+y-7=0.
7.2. l: ![]() , p: 4x-2y+23=0.
, p: 4x-2y+23=0.
7.3. l: ![]() , p: 10x-3y+9=0.
, p: 10x-3y+9=0.
7.4. l: ![]() , p: 3x-2y+13=0.
, p: 3x-2y+13=0.
7.5. l: ![]() , p: 3x-4y+7=0.
, p: 3x-4y+7=0.
7.6. l: ![]() , p: 2x+2y-13=0.
, p: 2x+2y-13=0.
7.7. l: ![]() , p: x-y-7=0.
, p: x-y-7=0.
7.8. l: ![]() , p: 2x-y+3=0.
, p: 2x-y+3=0.
7.9-16.Провести касательные к линии l , перпендикулярные прямой p.
7.9. l: ![]() , p: x-2y+9=0.
, p: x-2y+9=0.
7.10. l: ![]() , p: 2x-2y-5=0.
, p: 2x-2y-5=0.
7.11. l: ![]() , p: 4x+3y-7=0.
, p: 4x+3y-7=0.
7.12. l: ![]() , p: 4x+2y-1=0.
, p: 4x+2y-1=0.
7.13. l: ![]() , p: y-2x-4=0.
, p: y-2x-4=0.
7.14. l: ![]() , p: 3x-2y-6=0.
, p: 3x-2y-6=0.
7.15. l: ![]() , p: 5x+2y+8=0.
, p: 5x+2y+8=0.
7.16. l: ![]() , p: x+y-17=0.
, p: x+y-17=0.
7.17-21.Через точку М провести касательную к линии l .
7.17. M(-9;3), l: ![]() .
.
7.18. M(
2;2), l: ![]() .
.
7.19. M(0;-6), l: ![]() .
.
7.20. M(0;11), l: ![]() .
.
7.21. M(
7;0), l: ![]() .
.
7.22-25.Вывести условие, при котором прямая y=kx+b касается линии l .
7.22. l
: ![]() .
.
7.23. l
: ![]() .
.
7.24. l
: ![]() .
.
7.25. l
: ![]() .
.
8. Определить параметры, входящие в уравнения прямых и плоскостей, используя данные об их взаимном расположении.
8.1
![]()
![]()
![]()
![]()
![]()
8.2
![]()
![]()
![]()
![]()
![]()
8.3
![]()
![]()
![]()
![]()
![]()
![]()
![]()
8.4
![]()
![]()
![]()
![]()
8.5
![]()
![]()
![]()
![]()
![]()
![]()
8.6
![]()
![]()
![]()
![]()
![]()
8.7
![]()
![]()
![]()
![]()
![]()
8.8
![]()
![]()
![]()
![]()
![]()
![]()
8.9
![]()
![]()
![]()
![]()
![]()
![]()
8.10
![]()
![]()
![]()
![]()
![]()
![]()
8.11
![]()
![]()
![]()
![]()
8.12
![]()
![]()
![]()
![]()
![]() )
)
![]()
8.13
![]()
![]()
![]()
![]()
8.14
![]()
![]()
![]()
![]()
8.15
![]()
![]()
![]()
![]()
8.16
![]()
![]()
![]()
![]()
8.17
![]()
![]()
![]()
![]()
-

-

-

-



 -
пересекаются
-
пересекаются -
 p
и q
– пересекаются
p
и q
– пересекаются -
 p
и q
– пересекаются
p
и q
– пересекаются -

-

9.
Составить уравнение плоскости
![]() и найти расстояние точки N
от неё. Выяснить, лежат ли точка N
и начало координат по одну или по разные
стороны относительно плоскости
и найти расстояние точки N
от неё. Выяснить, лежат ли точка N
и начало координат по одну или по разные
стороны относительно плоскости
![]() .
.
9.1
А![]() .
.
9.2
![]() .
.
9.3
![]() .
.
9.4
![]() линии
пересечения плоскостей
линии
пересечения плоскостей
![]() .
.
9.5
![]() .
.
9.6
![]() .
.
9.7
![]() .
.
9.8
![]() .
.
9.9
![]() .
.
9.10
![]()
![]() проходит через линию пересечения
плоскостей
проходит через линию пересечения
плоскостей
![]() .
.
9.11
![]() .
.
9.12
![]()
![]() .
.
9.13
![]() .
.
9.14
![]() .
.
9.15
![]() .
.
9.16
![]() .
.
9.17
![]() .
.
9.18
![]() .
.
9.19
![]() .
.
9.20
![]() .
.
9.21
![]() .
.
9.22
![]() .
.
9.23
![]() .
.
9.24
![]() .
.
9.25
![]()
10.Составить канонические, параметрические или общие уравнения прямой р,проходящей через точку N, используя данные о расположении p относительно других объектов.
-
N (-1,2,-3) , p|| q:
 .
. -
N (2,2,5) , p

 ={1,2,0},
={1,2,0},
 ={0,3,7}.
={0,3,7}. -
N (1,0,5) , p||
 :
3x-y+7z=0
, p
пересекается с прямой
:
3x-y+7z=0
, p
пересекается с прямой
q: ![]() =
=![]() =
=![]()
-
N (2,-3,1) , p

 ={2,1,-1}
, p
пересекается
с прямой q:
={2,1,-1}
, p
пересекается
с прямой q: .
. -
N (3,1,0) , p||
 :
x-3y+z-1=0
, p||
:
x-3y+z-1=0
, p|| :
2x+3y+z+3=0.
:
2x+3y+z+3=0. -
N (4,-3,1) , p||
 :
x+2y-3z-1=0
, p
пересекается с прямой
:
x+2y-3z-1=0
, p
пересекается с прямой
 .
. -
N (5,7,-5) , p
 q:
q:
 =
= =
= , p
и q
– пересекаются.
, p
и q
– пересекаются. -
N (3,2,-2) , p пересекается с прямыми q:
 и r:
и r: .
. -
N (4,1,-3) , p

 ={3,-2,1}
, p
пересекается с прямой
q:
={3,-2,1}
, p
пересекается с прямой
q:
 =
= =
= .
. -
N (5,7,3) , p пересекается с прямой q:
 и
p
и
p q.
q. -
N (7,1,1) , p

 ={3,4,-1}
, p||
={3,4,-1}
, p|| :
2x-3z+6=0.
:
2x-3z+6=0. -
N (-2,3,1) , p

 :
3x+y+3=0 , p||
:
3x+y+3=0 , p|| :
2y-z+1=0.
:
2y-z+1=0. -
N (4,2,1) , p

 ={7,1,2}
, p
={7,1,2}
, p q:
q:
 .
. -
N (2,3,2) , p
 :
3x-2y+z-2=0 , p
:
3x-2y+z-2=0 , p ={2,0,1}.
={2,0,1}. -
N (-3,-,5) , p||
 :2x-3y-z+1=0
, p
:2x-3y-z+1=0
, p q:
q: .
. -
N (1,7,9) , p
 q:
q: , p
и q
–пересекаются.
, p
и q
–пересекаются. -
N (2,-3,-5) , p
 ={2,-1,-3}
, p
={2,-1,-3}
, p q:
q:
 .
.
10.18
N
(7,-3,1) , p![]() ={1,-1,2}
, p
пересекается с прямой q:
={1,-1,2}
, p
пересекается с прямой q:![]() .
.
10.19
N
(-1,2,1) , p![]() ={3,5,1}
, p
={3,5,1}
, p
![]() ={1,2,2}.
={1,2,2}.
10.20
N
(6,3,7) , p![]() :3x-y+z-2=0
, p
:3x-y+z-2=0
, p![]() q:
q:![]() =
=![]() =
=![]() .
.
-
N (4,2,2) , p
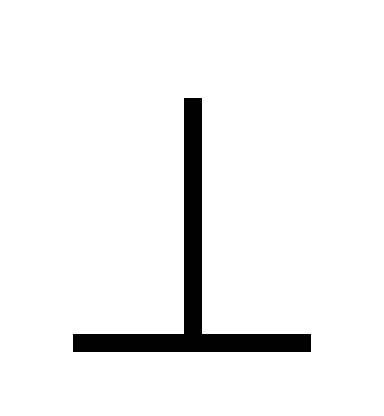 q:
q: ,
p
,
p r:
r: =
= =
= .
. -
N (1,1,3) , p||
 :2x-3y-z=0 , p
:2x-3y-z=0 , p q:
q: .
. -
N (5,0,1) , p||
 :x-3y+z=0
, p||
:x-3y+z=0
, p|| :2x+3z-1=0.
:2x+3z-1=0. -
N=q

 , где q:
, где q: =
= =
= ,
,
 :2x+7y-z+0
,p|| r:
:2x+7y-z+0
,p|| r: .
. -
N=q

 , где,
, где,
 :
x+2y+z-13=0
, p
:
x+2y+z-13=0
, p .
.
11.
Найти угол между прямой р
из задачи
10 и плоскостью
![]() из
задачи 9.
из
задачи 9.
12.1-4.
Найти проекцию точки М на прямую р или
плоскость
![]() .
.
![]()
![]()

![]()
12.5-7.Найти расстояние от точки M до прямой p.
![]()
![]()

12.8-11.Найти
точку N
, симметричную точке М относительно
плоскости
![]() или прямой р .
или прямой р .
![]()
![]()
![]()

12.12-15.Не находя точку пересечения , доказать , что прямые p и q пересекаются.
![]()
![]()


12.16-18.Составить
уравнение плоскости
![]() ,проходящей
через прямую р и параллельную прямой
q.
,проходящей
через прямую р и параллельную прямой
q.

![]()

12.19-22.Найти расстояние между прямыми p и q .

![]()


12.23-25.Составить
каноническое уравнение проекции прямой
р на плоскость
![]() .
.
![]()
![]()

Список рекомендованной литературы
1.Ильин В.А., Позняк Э.Г. Аналитическая геометрия . –М.: Наука . –223с.
2.Пак В.В., Носенко Ю.Л. Вища математика : Підручник . –К.: Либідь, 1996. –440с.
3.Клетеник Д.В. Сборник задач по аналитической геометрии. - СПб.: Спец. лит.,1998. –200с.
4.Цубербиллер О.Н. Задачи и упражнения по аналитической геометрии. –М.: Наука , 1970. –336с.
5.Сборник задач по математике для ВТУЗов . Линейная алгебра и основы математического анализа . / Под ред. Ефимова А.В., Демидовича Б.П. – М.:Наука,1986. -462 с.
6.Кузнецов Л.А. Сборник заданий по высшей математике . –М.: Высш.шк., 1983. –175с.
7.Ефимов Н.В. Краткий курс аналитической геометрии . –М. : Наука , 1975. –272с.
