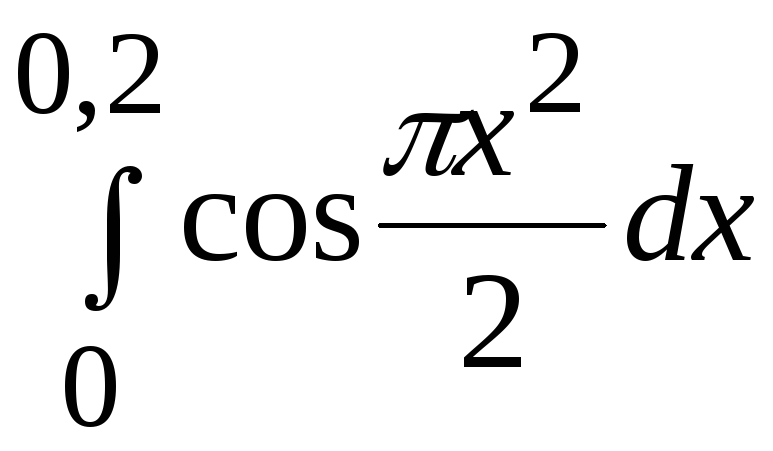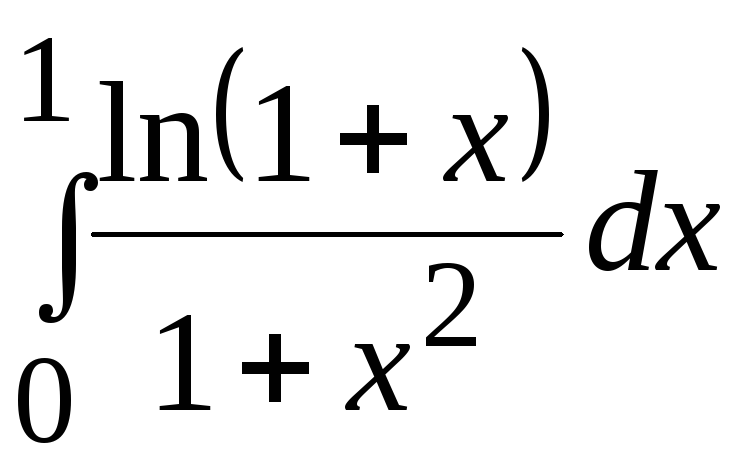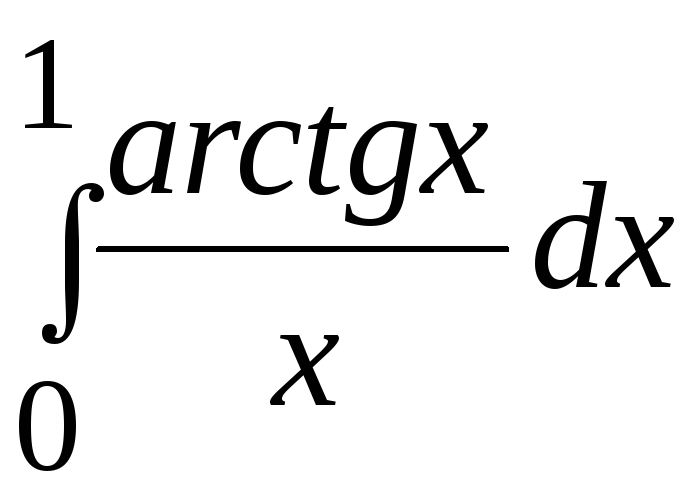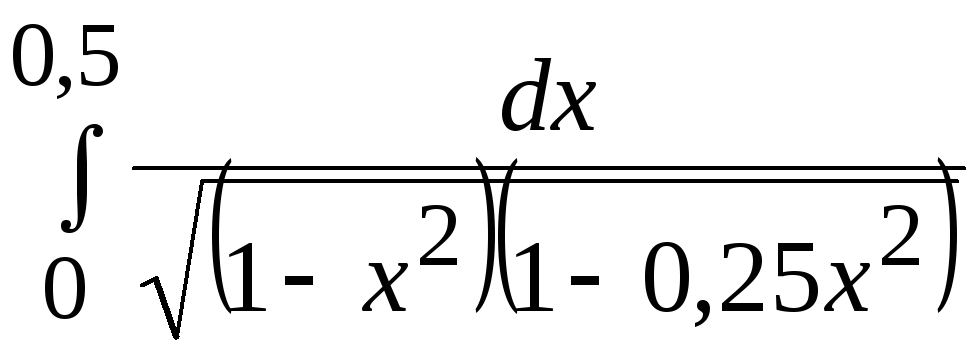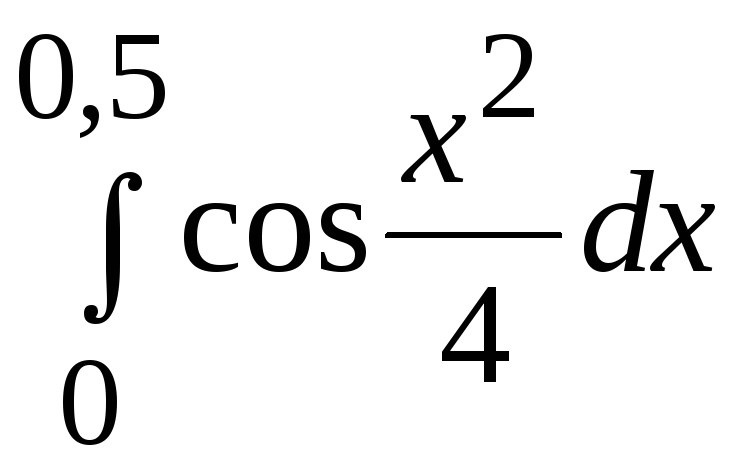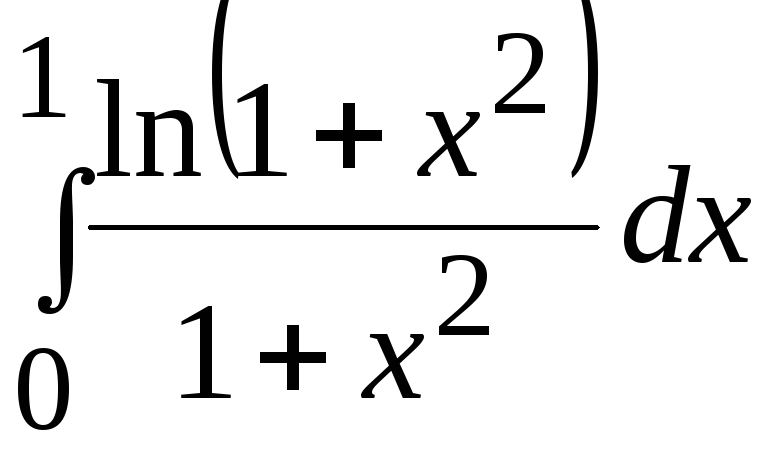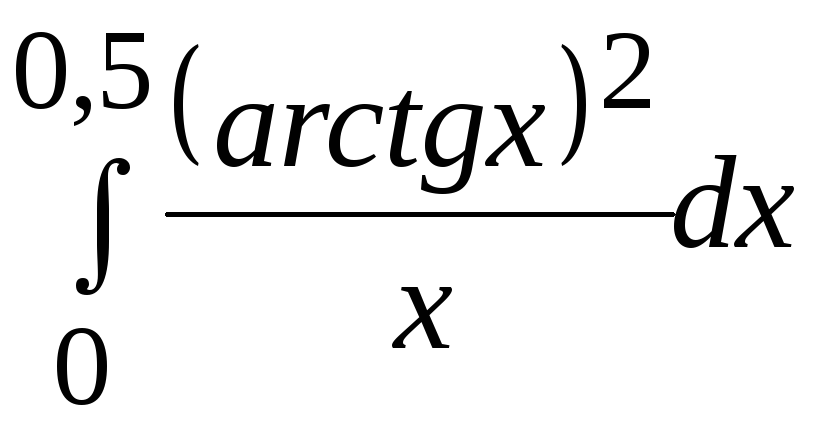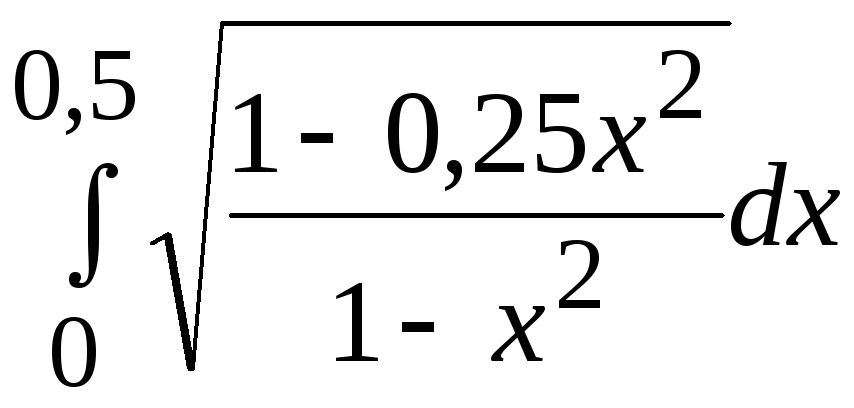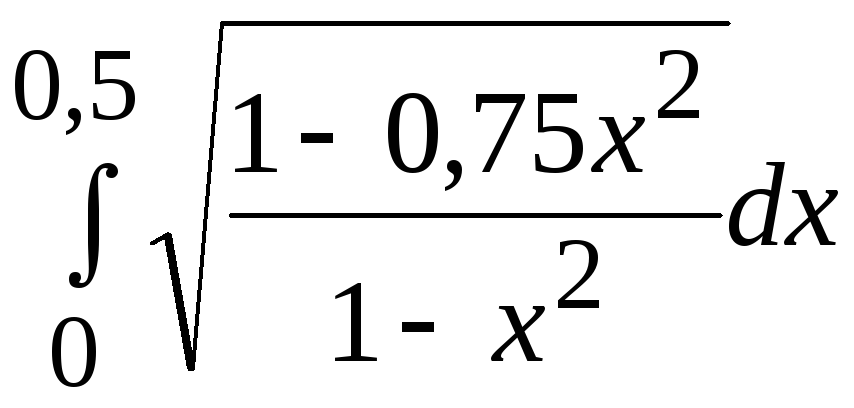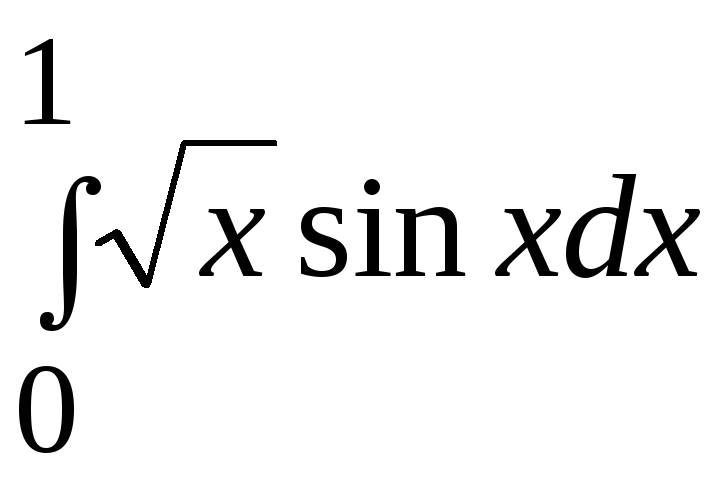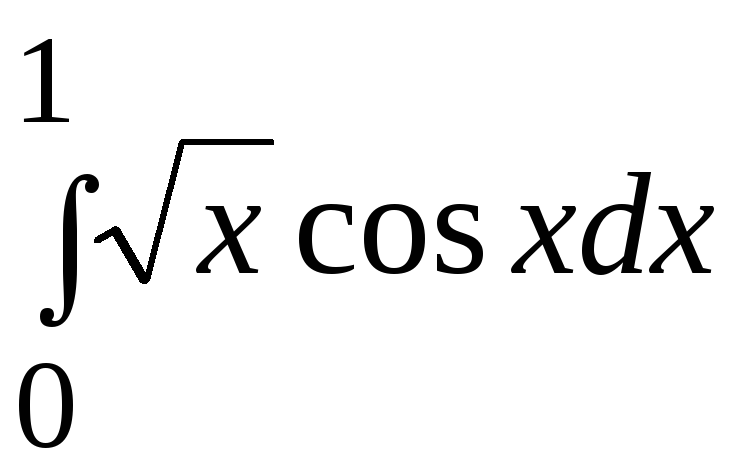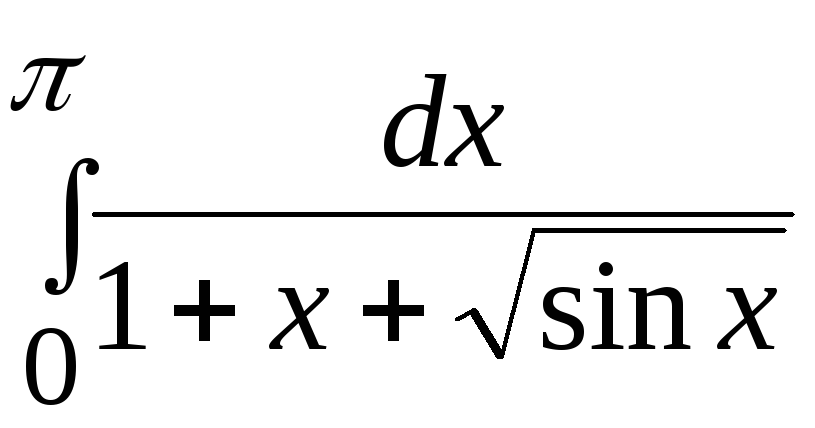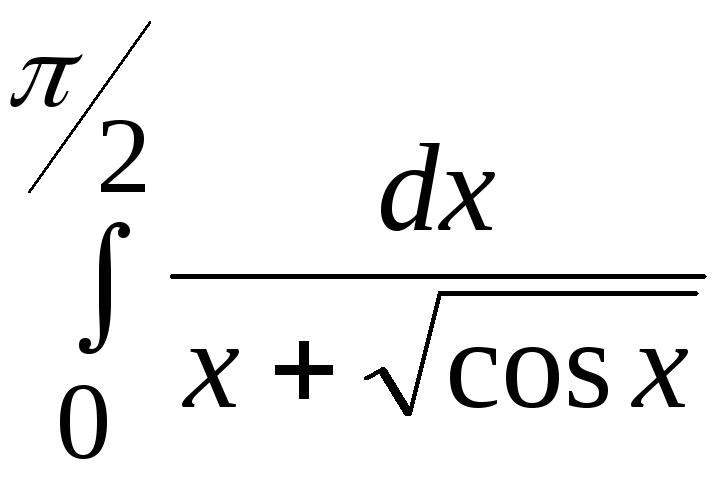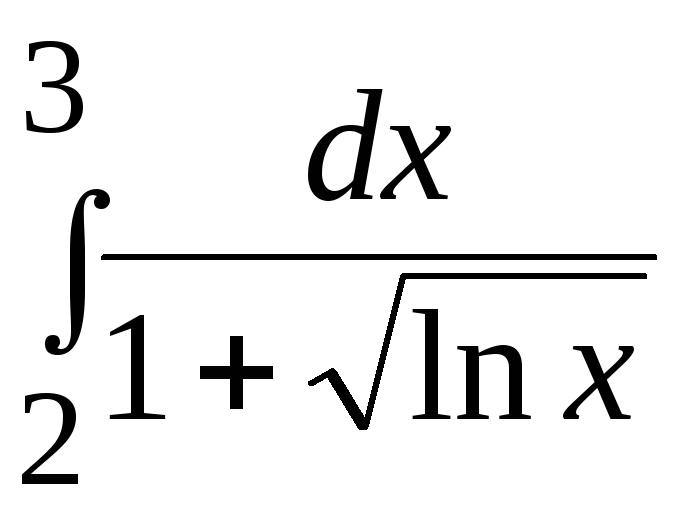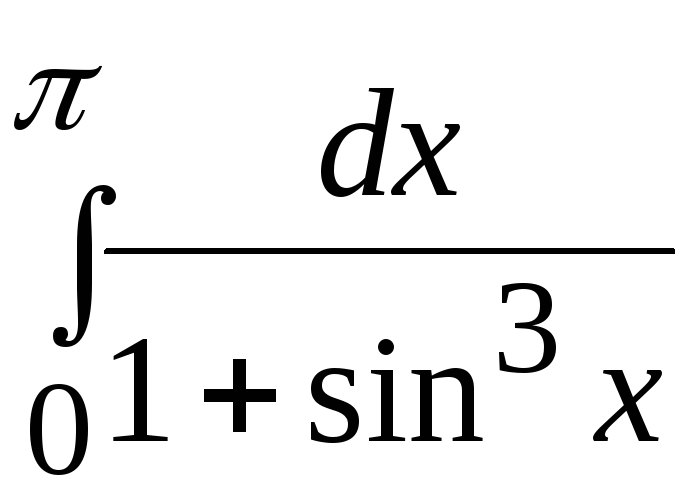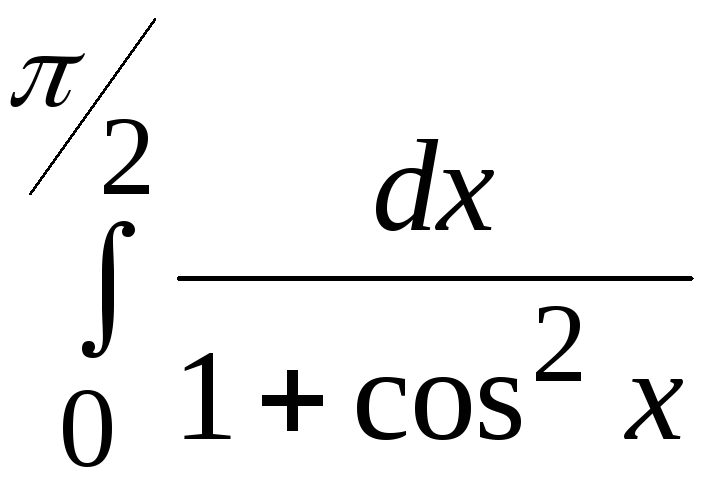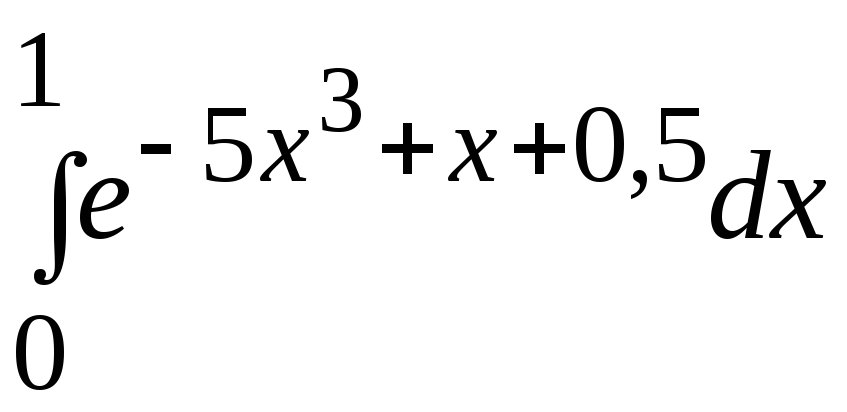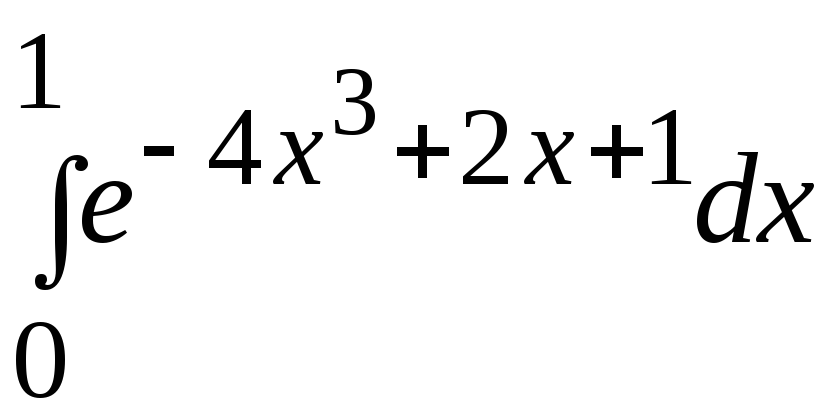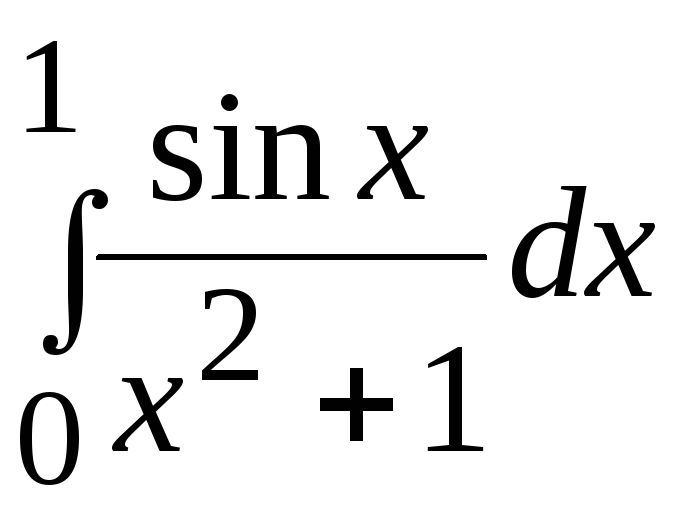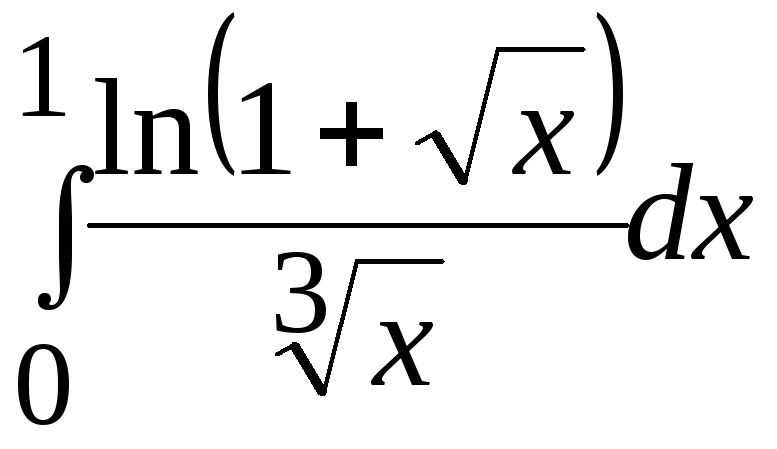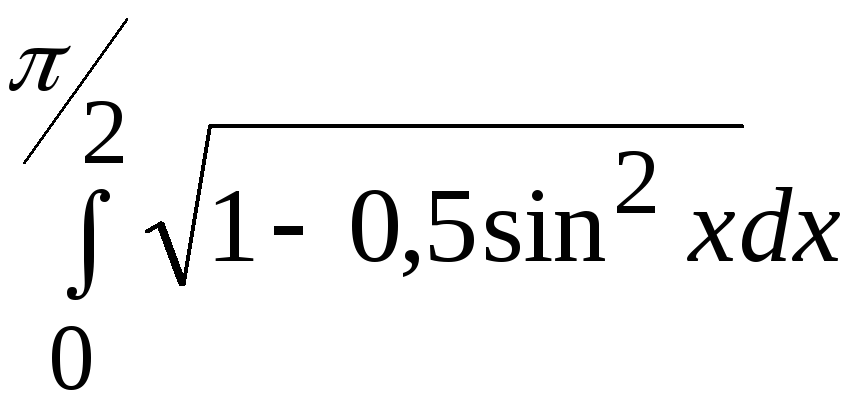5-Intergraly / LABY_po_Ch_met_5
.docЛАБОРАТОРНАЯ РАБОТА № 5
Задание
1. Применяя ручной просчет, вычислить значение заданного определенного интеграла (согласно варианту задания) с точностью 0,005*(1+k MOD 6) одним из 3-х методов:
1) прямоугольников;
2) трапеций;
3) Симпсона.
Метод выбрать по формуле: (k-1)MOD 3+1. k – номер студента в списке группы.
Построить график подынтегральной функции на отрезке интегрирования. Необходимое количество разбиений отрезка интегрирования для каждого из методов найти, используя соответствующие формулы для погрешности. Привести все промежуточные вычисления и построить графики всех необходимых функций.
2. Составить программу, вычисляющую значение данного интеграла тремя указанными методами с произвольно заданной точностью. Контроль точности производить по методу Рунге (двойного просчета):
|IN-I2N|/(2m-1) < e,
где IN и I2N – значения интеграла, найденные с числом подотрезков, равным соответственно N и 2N; m – порядок точности метода.
Входные данные программы: значение допустимой погрешности и начальное количество разбиений отрезка интегрирования (одинаковое для всех методов). Выходные данные: значение интеграла, найденные каждым методом и конечное число подотрезков для каждого метода.
Результаты расчетов свести в итоговую таблицу:
|
|
Методы |
||
|
Прямоугольников |
трапеций |
Симпсона |
|
|
Значение интеграла |
|
|
|
|
Кол-во разбиений |
|
|
|
Варианты заданий
Варианты заданий
Вопросы к защите лабораторной работы №5
«Численное интегрирование»
-
Простейшие квадратурные формулы (формулы правых, левых, центральных прямоугольников, формула трапеций, формула Симпсона), геометрическая иллюстрация, оценки погрешности. Точность квадратурных формул.
-
Квадратурные формулы интерполяционного типа: вывод формул, оценки погрешности.
-
Квадратурные формулы Гаусса: вывод формул, точность формул.
-
Метод Монте-Карло.