Материальный и тепловой балансы бинарной ректификации. Расчет числа теоретических ступеней.
Температура исходной смеси, содержащей 0,246 мол.доли муравьиной кислоты, равна (определена по диаграмме t-x-y):
С
помощью приведенных физических свойств
веществ (данные по изобарному равновесию
пар-жидкость для системы муравьиная –
уксусная кислота, теплоты испарения
чистых муравьиной и уксусной кислоты,
теплоемкость раствора в зависимости
от концентрации более летучего компонента)
можно рассчитать (принимая за стандартное
состояние компонентов в жидком виде
при
)
энтальпии смесей муравьиной и уксусной
кислот.
Так как данные по теплотам смешения муравьиной и уксусной кислоты отсутствуют, то уравнение преобразуется к виду:
Аналогично находим температуру и энтальпию кубового остатка. Для определения энтальпий дистиллята и пара, поступающего в дефлегматор с верхней тарелки по уравнениям:
Материальный баланс:
где
расходы,
соответственно, дистиллята, питания и
кубового остатка;
концентрация
более летучего компонента, соответственно,
в дистилляте, питании и кубовом остатке.
из этой системы уравнений получаем:
Тепловой баланс:
где
тепловые нагрузки дефлегматора и
кипятильника;
энтальпия пара, поступающего в дефлегматор;
потери
тепла, которые в нашей задаче принимаем
равными нулю.
Т.к.
исходная смесь подается при температуре
кипения, то
,
где
-
коэффициент характеризующий
термодинамическое состояние питания
ректификационной колонны.
Определение числа теоретически ступеней при допущении постоянства мольных расходов.
В этом случае расходы пара и жидкостей в укрепляющей части колонны равны:
Для исчерпывающей части колонны мольные расходы пара и жидкости можно найти из следующих уравнений:
При постоянстве мольных расходов уравнение материального баланса (уравнение рабочих линий), описываются для аппаратов со ступенчатым контактом фаз следующими линейными зависимостями:
-
для укрепляющей части;
-
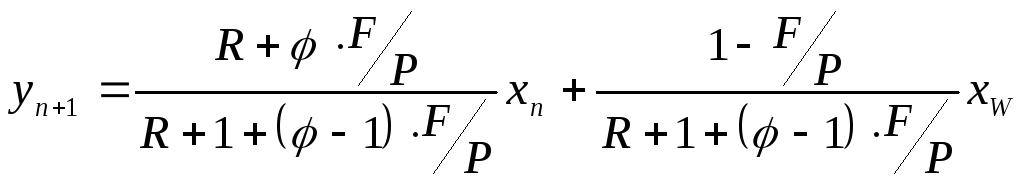
для исчерпывающей части
Схема расчета: [1] стр. 61
Точный расчет числа теоретических ступеней основан на модели ректификационной колонны со ступенчатым контактом фаз, причем каждая ступень принимается теоретической. Расчет заключается в последовательном определении, от ступени к ступени, расходов, составов и энтальпий фаз с помощью уравнения фазового равновесия:
а также материального и теплового балансов. Для верхней (укрепляющей) части колонны уравнение внутреннего материального и теплового баланса имеет вид:
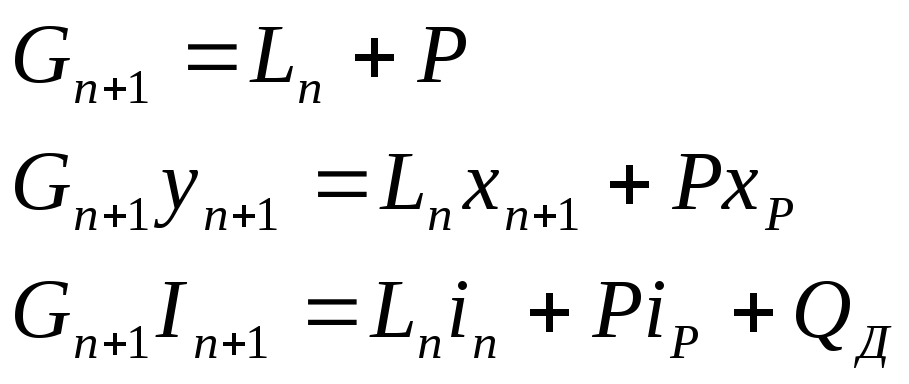
Для нижней (исчерпывающей) части колонны соответствующие уравнения образуют следующую систему:
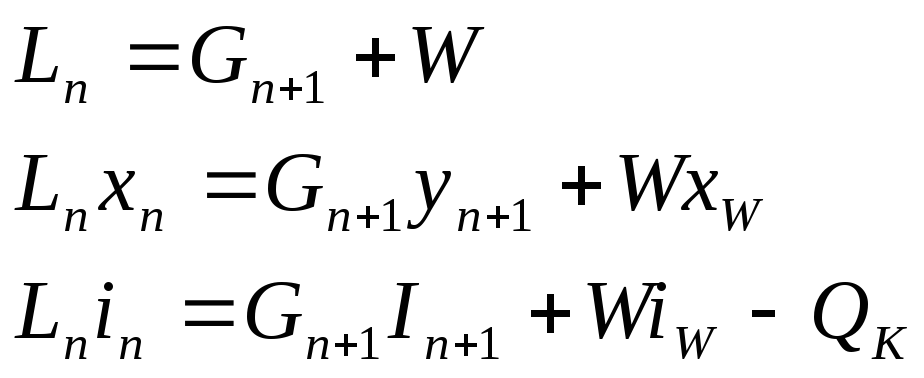
В этих системах не учтены потери тепла.
Одна из возможных схем точного расчета числа теоретических ступеней для процесса бинарной ректификации: [1] стр. 59
Сначала
из материального баланса определяются
расходы дистиллята и кубового остатка.
При полной конденсации паров в дефлегматоре
должно соблюдаться следующее условие:
Это
уравнение позволяет найти состав пара,
уходящего с верха колонны, и состав
флегмы. По составу пара можно найти
температуру его конденсации
.
При этой температуре будет выходить
пар с первой ступени. Температуру флегмы
можно принять равной
(если пренебречь ее переохлаждением в
флегме). Знание температур и составов
пара, поступающего в дефлегматор, и
флегма дает возможность определить их
энтальпии
.
Расходы пара
и
флегмы
определяются флегмовым числом:
Теперь можно найти тепловые нагрузки дефлегматора и кипятильника, рассчитав энтальпии исходной смеси и кубового остатка (энтальпия дистиллята при полной конденсации паров в дефлегматоре равна энтальпии флегмы). После этих предварительных вычислений проводиться последовательный расчет составов, расходов, температур и энтальпий фаз для всех ступеней.
Сначала
с помощью равновесных данных находим
состав жидкости, выходящей с первой
«теоретической ступени»:
.
Температура этой жидкости должна быть
равна
.
Расход ее, а также расход, состав и
температура пара, поступающего на первую
ступень со второй, определяется системой
уравнений внутреннего материального
баланса для укрепляющей части колонны.
Решив эту систему при
находим
.
Далее переходим к второй ступени и их
условия равновесия находим
.
Опять решаем систему при
,
определяем
.
Затем переходим к третьей ступени и так
далее.
Так рассчитываем для ступеней, пока не достигнем состава на тарелке питания, номер той ступени, который будет этому соответствовать, и будет номером тарелки питания. Дальше расчет ведут по уравнениям для нижней части колонны. Расчет продолжается до тех пор, пока содержание легко летучего компонента в жидкости, стекающей с какой-либо ступени, не станет меньше его содержания в кубовом остатке. Номер этой ступени равен числу теоретических ступеней, при котором кубовый остаток содержит не более заданного количества легколетучего компонента.
При расчете этой главы использовалась программа Рабирек-7 «Материальный и тепловой балансы бинарной ректификации. Расчет числа теоретических ступеней».