Государственное высшее учебное заведение

«Донецкий национальный технический университет»

Факультет компьютерных наук и технологий

Кафедра «Вычислительная математика и программирование»

Курсовая работа

по курсу:«Вычислительная техника и алгоритмические языки»

на тему:

«Использование метода наименьших квадратов при решении электротехнических задач»

Студента первого курса

группы

направления подготовки 6.050702

специальности 7.05070204

Руководитель Чеснокова Оксана Витальевна

Национальная шкала _______________

Количество баллов: ___ Оценка: ECTS ___

Членыкомисии ________________ __________________

(подпись) (фамилия и инициалы)

________________ __________________

(подпись) (фамилия и инициалы)

________________ __________________

(подпись) (фамилия и инициалы)

г. Донецк – 2014

Анотация

В данной курсовой работе я рассмотрел задачу о зависимости тока ротора АД АИУМ225М4 от напряжения при различных коэффициентах нагрузки. Составил программудля вычисления коэффициента корреляции,подбора методом наименьших квадратов.Контрольный расчет был проведен при помощи математического пакетаMathCad.

Содержание

Анотация 2

Введение 4

1.Постановка задачи 5

2.Описание математической модели решения задачи 6

3.Блок-схема алгоритма 13

4.Описание программы 18

4.1.Описание алгоритма программы 18

4.2.Описание выполнения программы 19

1.Характеристика данных и их условные обозначения 21

2.Текст программы 22

3.Контрольный пример 31

4.Анализ результатов 35

Заключение 36

Список литературы 37

Приложение 38

Введение

В работе рассматривается решение задачи по обработке реальных количественных экспериментальных данных, полученных в результате технических испытаний, методом найменьших квадратов. В качестве инструмента для решения поставленной задачи выбраны язык программирования С++ и математический пакет MathCAD.

1.Постановка задачи

Известны зависимости тока ротора АД АИУМ225М4 от напряжения при различных коэффициентах нагрузки.

Для зависимостей с коэффициентами нагрузки 1, 1,3 вычислить коэффициент корреляции; методом наименьших квадратов подобрать зависимости вида, вычислить индекс корреляции, суммарную квадратичную ошибку, среднюю ошибку в точке и относительную ошибку. Найти ожидаемое значение токов при напряжениях 0,72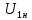, 0,98, 1,23. Номинальной ток ротора 52 А.

В программе исходные данные рекомендуется считывать из файла aium225m4.txt или с клавиатуры. Результаты вычислений сохранить в текстовом файле rezult.txt. Средствами математического пакета или электронных таблиц проверить результаты работы программы, построить график экспериментальной зависимости и подобранной функции.

Рисунок 1.График исходных данных

2.Описание математической модели решения задачи

Метод наименьших квадратов используется при обработке реальных количественных данных, полученных в результате всевозможных научных опытов, технических испытаний, астрономических, геодезических и т.п. наблюдений. Пусть в результате эксперимента были получены некоторые данные, представленные в виде таблицы . Необходимо построить аналитическую зависимость, наиболее близко описывающую результаты эксперимента.

Таблица 1– экспериментальные данные

Идея метода наименьших квадратов заключается в том, что функцию

необходимо подобрать таким образом, чтобы сумма квадратов отклонений измеренных значений yi от расчетных Yi была наименьшей:

Рисунок 2.Визуализация метода найменьших квадратов

Геометрическая интерпретация метода наименьших квадратов Задача сводится к определению коэффициентов . Для ее решения необходимо составить систему уравнений

Если параметры ai входят в зависимостьлинейно, то получим систему из k-линейных уравнений с k неизвестными:

Зная коэффициенты, являющиеся решением системы , можно составить искомую функцию

Подбор параметров линейной функции

Пусть необходимо определить параметры функци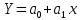и: . Составим многочлен для заданной функции:

Сформируем систему линейных уравнений , решив которую, определим коэффициенты функции:

Кубическая функция

Необходимо определить параметры многочлена третьей степени:

Составим функцию

Система уравнений для вычисления параметров 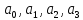примет вид:

Полином k-й степени

Необходимо определить параметры многочлена k-й степени:

Тогда система уравнений для определения параметров ak принимает вид:

Получив коэффициенты полинома, необходимо произвести выравнивание значений экспериментальной зависимости, то есть выполнить расчет теоретических значений по полученной формуле.

Уравнение регрессии и коэффициент корреляции

Линия, описываемая уравнением вида y = a0 + a1x, называется линией регрессии y на x, параметры a0 и a1 называются коэффициентами регрессии и определяются формулами .

Чем меньше величина тем более обоснованно

предположение, что экспериментальные данные описываются линейной функцией. Существует показатель, характеризующий тесноту линейной связи между x и y, называемый коэффициентом корреляции и рассчитываемый по формуле:

Значение коэффициента корреляции удовлетворяет соотношению:

.

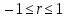Чем меньше отличается абсолютная величина r от единицы, тем ближе к линии регрессии располагаются экспериментальные точки. Если коэффициент корреляции равен нулю, то это означает, что между x и y не существует линейной связи, но между ними может существовать зависимость, отличная от линейной.

Криволинейная корреляция

Обычно коэффициент корреляции r применяется только в тех случаях, когда между данными существует прямолинейная связь. Если же связь криволинейная, то пользуются индексом корреляции, который рассчитывается по формуле:

где y– экспериментальные значения,

Y – теоретические значения,

–среднее значение y.

Индекс корреляции по своему абсолютному значению колеблется в пределах от 0 до 1. При функциональной зависимости индекс корреляции равен 1. При отсутствии связи R = 0. Если коэффициент корреляции r является мерой тесноты связи только для линейной формы связи, то индекс корреляции R – и для линейной, и для криволинейной. При прямолинейной связи коэффициент корреляции по своей абсолютной величине равен индексу корреляции:.