
- •Раздел 1.Статика- это раздел механики, в котором изучаются методы преобразования систем сил в эквивалентные системы и устанавливаются условия равновесия сил, приложенных к твердому телу.
- •Задача 1. Определение реакций опор балки под действием плоской произвольной системы сил
- •2. Условия равновесия:
- •3. Составление уравнений равновесия:
- •Задача 2.Определение реакций опор составной конструкции
- •Раздел 2. Кинематика это раздел механики, в котором изучается движение материальных тел в пространстве с геометрической точки зрения, вне связи с силами, определяющими это движение.
- •6 Семестр. Основы расчета механизмов и машин. Сопротивление материалов— это наука об инженерных методах расчета на прочность, жесткость и устойчивость элементов конструкций.
- •2. Поперечная сила считается положительной, если она вращает отсеченную часть по ходу часовой стрелки и отрицательной, если вращение происходит против хода часовой стрелки.
- •3. Изгибающий момент положителен, если сжаты верхние волокна отсеченной части, и отрицателен, если сжаты нижние волокна. Эпюра изгибающих моментов строится на сжатых волокнах.
- •4. Правило знаков для крутящего момента удобно принимать произвольным.
- •Задача 1. Расчет на прочность бруса при растяжении
- •Задача 2. Расчет вала на прочность при кручении
- •Задача 3. Расчет балки на изгиб
- •7 Семестр. Основы построения механизмов и машин. Детали машин
- •1. Расчет прочности фрикционных передач
- •2. Расчет на прочность валов и осей
- •Российская академия образования
- •2. Расчет зубчатых цилиндрических колес редуктора
Раздел 2. Кинематика это раздел механики, в котором изучается движение материальных тел в пространстве с геометрической точки зрения, вне связи с силами, определяющими это движение.
Скорость — это векторная величина, характеризующая быстроту и направление движения точки в данной системе отсчета.
При неравномерном криволинейном движении точки изменяются модуль и направление ее скорости. Ускорение точки характеризует быстроту изменения модуля и направления скорости точки.
Поступательным движением твердого тела называется такое движе-ние, при котором любая прямая, проведенная в теле, остается во все время движения тела параллельной своему начальному положению.
Все точки твердого тела. движущегося поступательно описывают одинаковые (совпадающие при наложении) траектории и в каждый момент времени имеют геометрически равные скорости и ускорения.
Вращательным движением твердого тела называется такое его движение, при котором все точки, принадлежащие некоторой прямой, неизменно связанной с телом, остаются неподвижными.
Величина, характеризующая быстроту изменения угла поворота φ с течением времени, называется угловой скоростью тела.

Числовая величина, характеризующая быстроту изменения угловой скорости с течением времени, называется угловым ускорением тела.
Задача 1. Определение кинематических характеристик поступательного и вращательного движений твердого тела
Груз
1
(рис. 1),
опускаясь, согласно уравнению s
= 3
![]() +15,
где s
- расстояние груза от места схода нити
с поверхности вала в сантиметрах; t
- время в
секундах, приводит в движение колесо
2, ременную передачу, колесо 3 и рейку 4.
+15,
где s
- расстояние груза от места схода нити
с поверхности вала в сантиметрах; t
- время в
секундах, приводит в движение колесо
2, ременную передачу, колесо 3 и рейку 4.
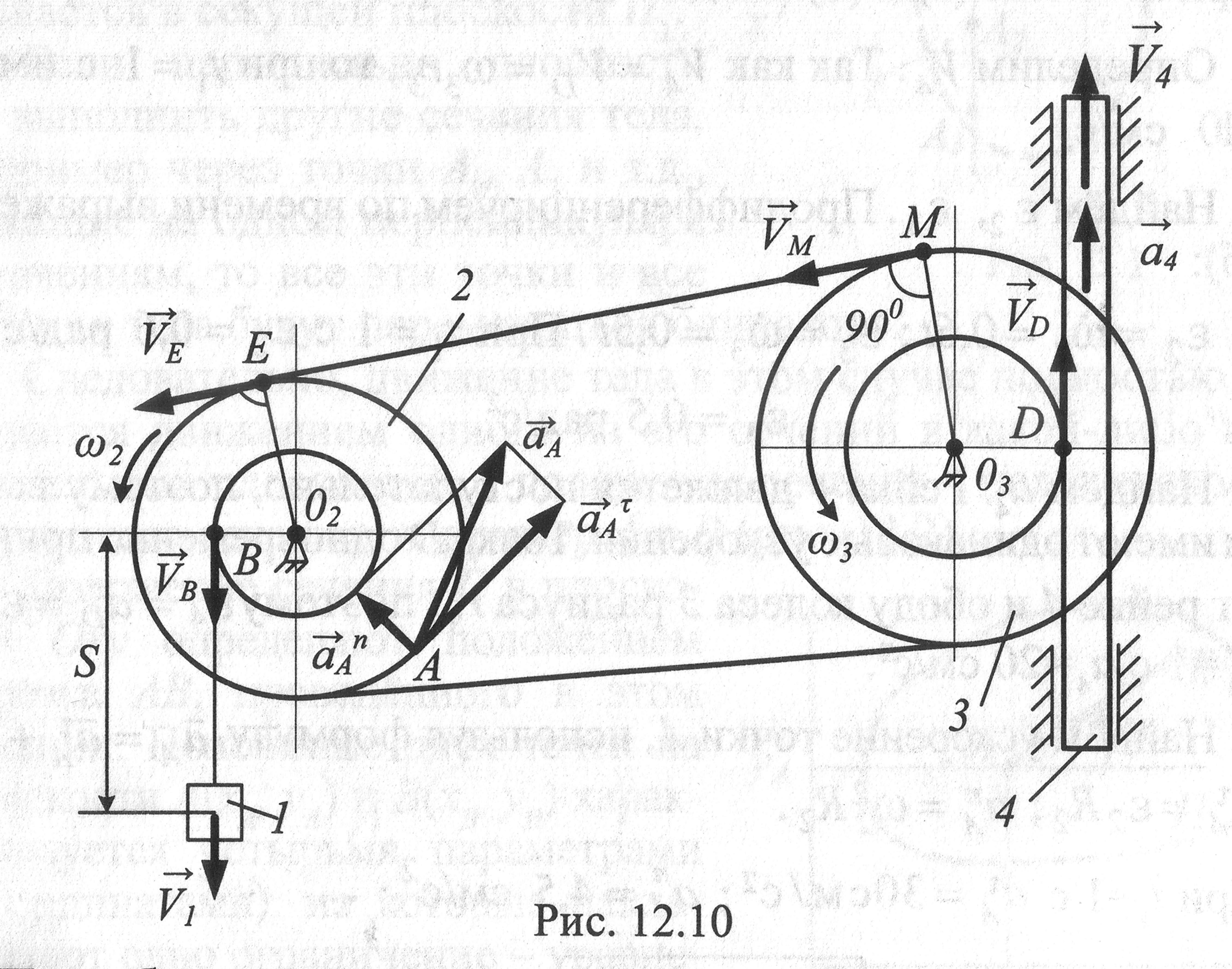
Рис.1
Пренебрегая
скольжением ремня по ободам колес,
определить для момента времени
![]() =1
с скорость и ускорение рейки 4, угловые
скорости и ускорения колёс 2, 3 и ускорение
точки А, если
=1
с скорость и ускорение рейки 4, угловые
скорости и ускорения колёс 2, 3 и ускорение
точки А, если
![]() =30
см;
=30
см;
![]() =50
см - радиусы
ступеней колеса 2;
=50
см - радиусы
ступеней колеса 2;
![]() =40
см;
=40
см;
![]() =60
см -
радиусы ступеней
колеса 3.
=60
см -
радиусы ступеней
колеса 3.
Дано:
![]() ;
;![]() =30
см;
=30
см;![]() =50
см;
=50
см;
![]() =40
см;
=40
см;
![]() =60
см.
=60
см.
Определить:
![]() при
при
![]() с.
с.
Найдём
 ,
, .
Зная уравнение
движения груза 1, определим его скорость
как функцию времени
.
Зная уравнение
движения груза 1, определим его скорость
как функцию времени
 =
= =
9
=
9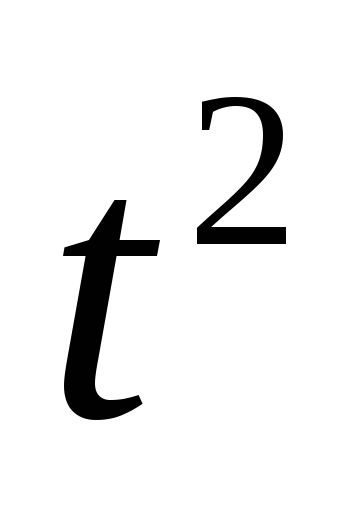 .
Груз подвешен на нерастяжимом канате,
поэтому скорость груза 1 такая же, как
скорости точек на ободе колеса 2 радиуса
.
Груз подвешен на нерастяжимом канате,
поэтому скорость груза 1 такая же, как
скорости точек на ободе колеса 2 радиуса
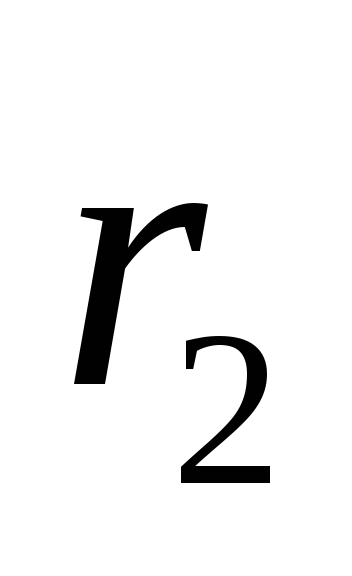 ,
т.е.
,
т.е.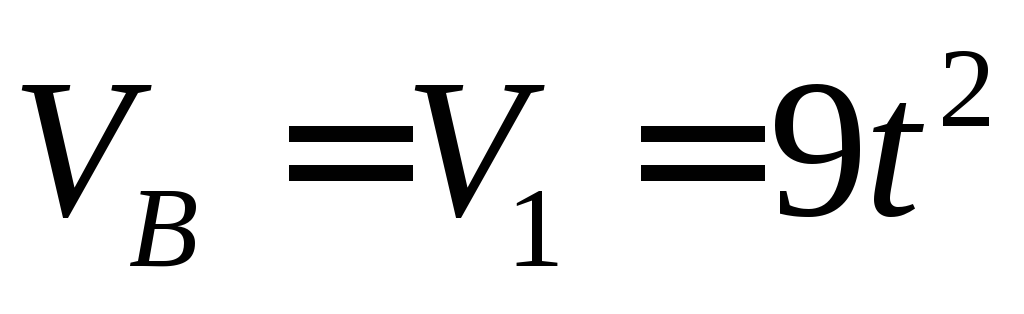 .
Найдем
.
Найдем как функцию времени:
как функцию времени:
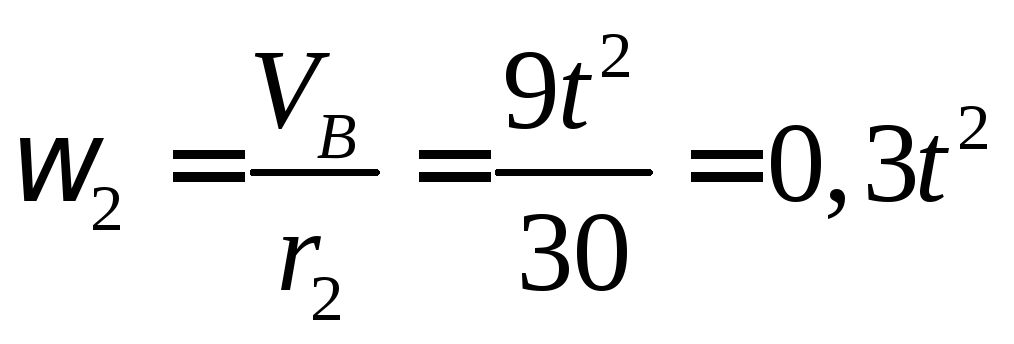 . (а)
. (а)
Так
как колёса 2 и 3 связаны ременной передачей
(ремень нерастяжим), то
![]() ,
но
,
но![]() ;
;![]() .
.
![]() ,
,
поэтому
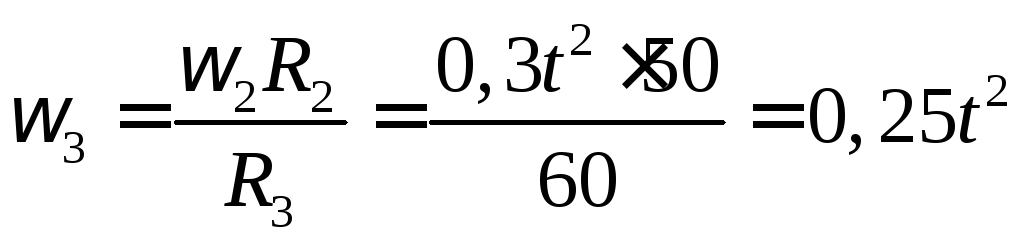 . (б)
. (б)
При
t=1
с из (а) и (б) найдем ![]() =
0,3 рад/с;
=
0,3 рад/с; ![]() =0,25
рад/c.
=0,25
рад/c.
Определим
 .
Так как
.
Так как =
=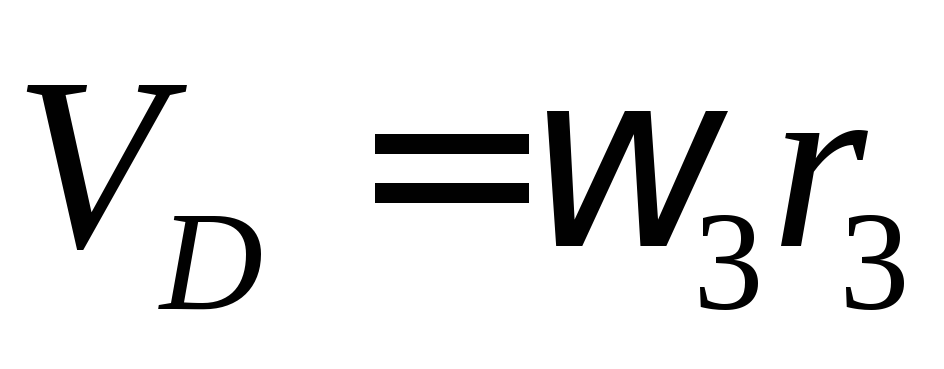 ,
то при
,
то при =1
с имеем
=1
с имеем =10
см/c.
=10
см/c.Найдем
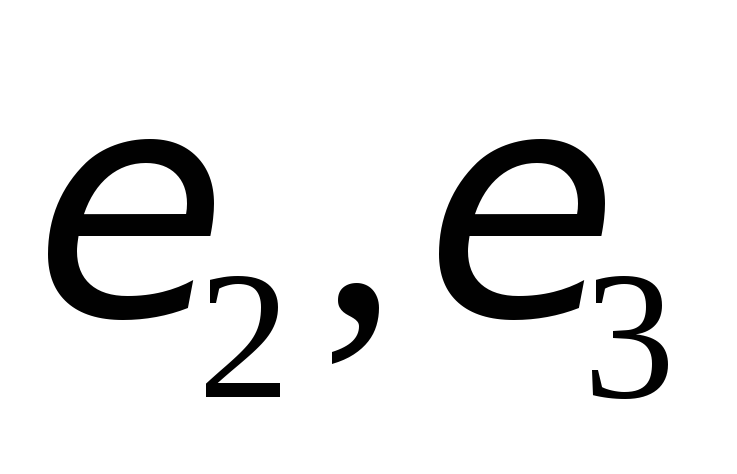 .
Продифференцируем по времени выражения
(а), (б):
.
Продифференцируем по времени выражения
(а), (б):
![]() ;
;
![]() .
При
.
При![]() =1с
=1с![]() =0,5
рад/
=0,5
рад/![]() .
.
Найдем
 .
Рейка 4 движется поступательно, поэтому
все её точки имеют одинаковые ускорения.
ТочкаD
одновременно принадлежит рейке 4 и
ободу колеса 3 радиуса
.
Рейка 4 движется поступательно, поэтому
все её точки имеют одинаковые ускорения.
ТочкаD
одновременно принадлежит рейке 4 и
ободу колеса 3 радиуса
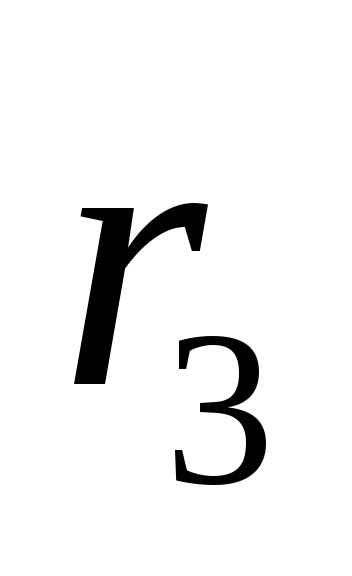 ,
поэтому
,
поэтому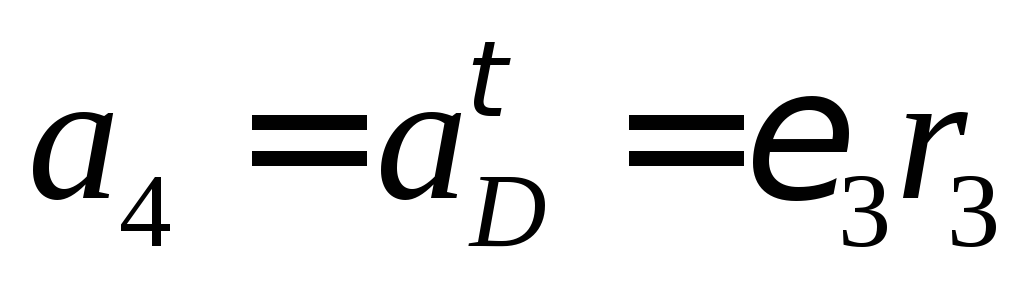 ;
при
;
при =1с
и
=1с
и =20
см/
=20
см/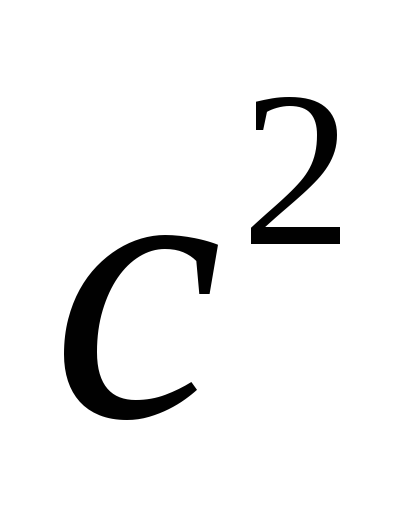
Найдем ускорение точки А, используя формулу
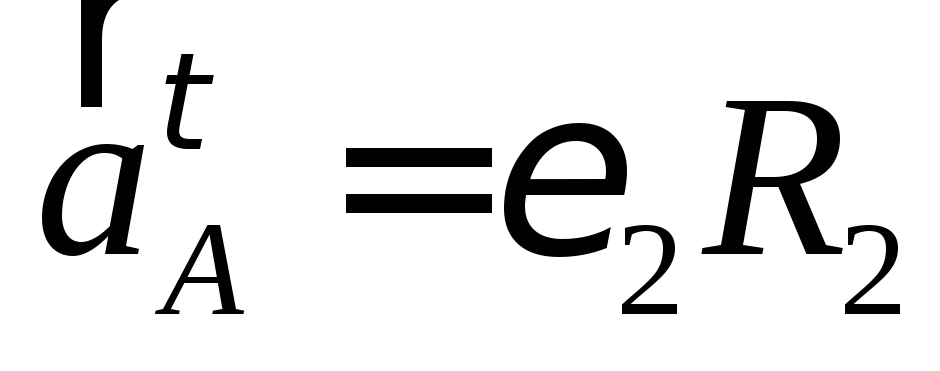 -вращательное
ускорение;
-вращательное
ускорение;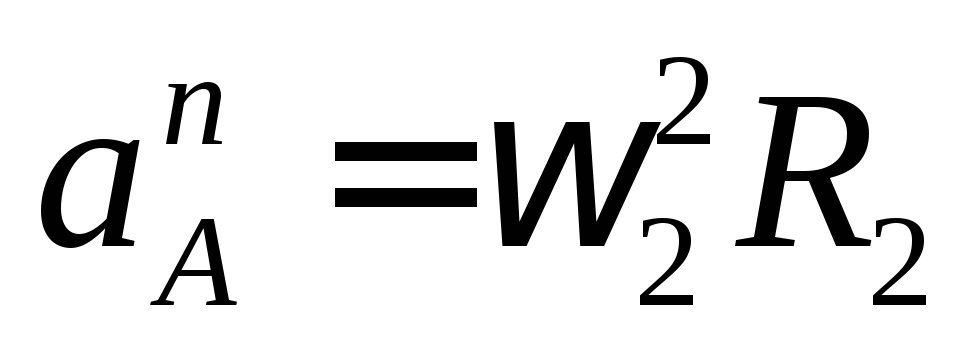 .-центростремительное
ускорение.
.-центростремительное
ускорение.
При
![]() =1с
и
=1с
и![]() =30
см/
=30
см/![]() ;
;![]() =4,5
см/
=4,5
см/![]() ;
;
![]() см/
см/![]() .
.
Раздел 3. Динамика раздел механики, в котором изучается движение материальных тел в пространстве в зависимости от действующих на них сил.
Задача 1. Применение теоремы об изменении кинетической энергии к исследованию движения механической системы
Каток для раскатывания асфальта (рис. 1) состоит из кузова массой т1 = 3∙103 кг и двух одинаковых барабанов. Масса барабана m2=103 кг, радиус его r=0,5м, а радиус инерции ρ=0,4м. Коэффициент трения качения барабанов fк=9 см. Определить скорость кузова катка после того, как он проехал расстояние S=2 м, начальная скорость катка была равна 0,2 м/с. К ведущему барабану приложен постоянный момент M=4,6 кНм.
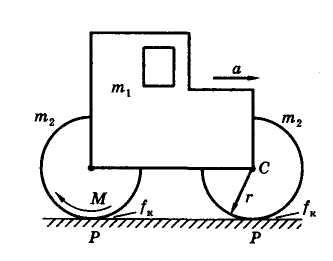
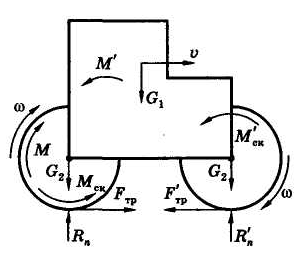
Рис. 1 Рис. 2
Решение. Так как в задаче идет речь о конечном перемещении системы, то следует применить теорему об изменении кинетической энергии в интегральной (конечной) форме:
![]() .
.
Кинетическая энергия системы (поступательно движущийся кузов и совершающие плоское движение барабаны) имеет вид
![]() ,
,
где v — скорость кузова, vС — скорость центра масс барабана, ω — его угловая скорость, JzC = m2ρ2 = 160 кгм2 — момент инерции барабана относительно его оси (проходящей через центр масс).
Кинематические связи определяются тем, что каждый барабан поворачивается вокруг своего мгновенного центра скоростей (точки Р), а именно: vC = ωr; кроме того, v = vC, т. е. ω = v/r. Тогда кинетическая энергия приводится к виду
![]() ,
,
где тпр= 6280 кг — приведенная к кузову масса системы. Начальная кинетическая энергия системы
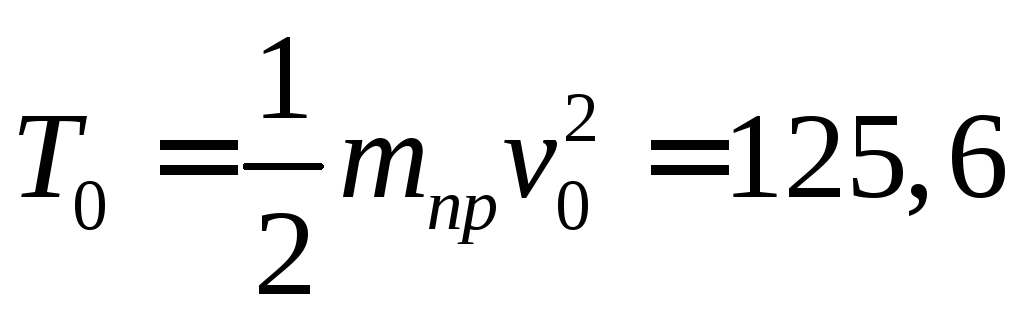 Дж.
Дж.
Вычислим теперь величину работы действующих сил (рис. 2).
Внешние
силы. Силы
тяжести барабанов G2
и кузова G1
работы не совершают, поскольку они
перпендикулярны скоростям (и,
соответственно, перемещениям) точек их
приложения. Также не работают нормальные
реакции Rn
и R’n
и силы трения Frp
и
![]() ,
так как всегда равны нулю скорости их
точек приложения — мгновенных центров
скоростей, и, соответственно, постоянно
равны нулю их мощности.
,
так как всегда равны нулю скорости их
точек приложения — мгновенных центров
скоростей, и, соответственно, постоянно
равны нулю их мощности.
Работу будут совершать моменты сопротивления качению:
![]() и
и
![]() ,
,
а именно:
![]() ,
,
где
![]() .
.
Здесь φ — угол поворота барабанов, для которого, интегрируя уравнение кинематической связи ω = v/r с учетом нулевых начальных условий для перемещений s и φ, легко получаем φ = s/r. Тогда
![]()
Внутренние силы. Запишем, учитывая, что кузов не вращается, суммарную работу внутренних сил (моментов) М и М’:
![]() .
.
Тогда сумма работ всех сил запишется в виде
![]() .
.
Множитель, стоящий в этой формуле перед перемещением s, — это приведенная сила системы
![]()
Итак
![]() Дж.
Дж.
Собирая правую и левую части теоремы, получаем
![]()
или Т – 125,6 = 760, откуда
![]() и
и
![]()
Ответ: v = 0,53 м/с.
