
- •Справочные материалы по курсу «Основы научных исследований оперативно-тактических действий»
- •1 Движения руки (рук), пальцев, кисти
- •2 Движения корпуса
- •3 Движение ног
- •4 Умственно – зрительная деятельность
- •5 Прилагаемое усилие г
- •Укрупнённые временные параметры выполнение некоторых видов действий
- •Коэффициенты Стьюдента
- •Необходимое число измерений для получения ошибки ∆ с надежностью p
- •Показатели работоспособности
- •Учет условий, выполнение нормируемых упражнений
- •Время открепления и снятия пожарного оборудования
- •Время выполнения операций с пожарным оборудованием
- •Время преодоления 1 м
- •Коэффициент, учитывающий высоту снежного покрова
- •Коэффициент, учитывающий влияние температуры окружающей среды
Справочные материалы по курсу «Основы научных исследований оперативно-тактических действий»
Таблица:
|
№ п/п |
Наименование |
Формула | |||||||||||||||||||||||||||||||||||||||||||||
|
1. |
Интервалы статистического ряда
|
| |||||||||||||||||||||||||||||||||||||||||||||
|
2. |
Выборочная средняя |
| |||||||||||||||||||||||||||||||||||||||||||||
|
3. |
Выборочная дисперсия |
| |||||||||||||||||||||||||||||||||||||||||||||
|
4. |
Среднее квадратичное отклонение
|
S
=
| |||||||||||||||||||||||||||||||||||||||||||||
|
5. |
Коэффициенты интенсивности освоения |
| |||||||||||||||||||||||||||||||||||||||||||||
|
6. |
Доверительный интервал
|
| |||||||||||||||||||||||||||||||||||||||||||||
|
7. |
Исключение грубых ошибок
|
| |||||||||||||||||||||||||||||||||||||||||||||
|
8.
|
Требуемое количество измерений |
| |||||||||||||||||||||||||||||||||||||||||||||
|
9. |
Критерий Фишера |
| |||||||||||||||||||||||||||||||||||||||||||||
|
10. |
Средняя арифметическая дисперсия
|
| |||||||||||||||||||||||||||||||||||||||||||||
|
11. |
Проверка однородности нескольких дисперсий
|
| |||||||||||||||||||||||||||||||||||||||||||||
|
12. |
Сравнение двух выборочных средних
|
| |||||||||||||||||||||||||||||||||||||||||||||
|
13. |
Число степеней свободы |
| |||||||||||||||||||||||||||||||||||||||||||||
|
14. |
Коэффициент корреляции
|
r
=
| |||||||||||||||||||||||||||||||||||||||||||||
|
15. |
Проверка гипотезы о корреляционной связи
|
| |||||||||||||||||||||||||||||||||||||||||||||
|
16. |
Определение количества переменных факторов |
q
=
| |||||||||||||||||||||||||||||||||||||||||||||
|
17. |
Интервалы между факторами
|
H
=
| |||||||||||||||||||||||||||||||||||||||||||||
|
18. |
Значение факторов, при которых необходимо проводить исследования |
q
=
| |||||||||||||||||||||||||||||||||||||||||||||
|
19. |
Физическая работоспособность |
| |||||||||||||||||||||||||||||||||||||||||||||
|
20. |
Графоаналитический метод установления уравнения регрессии а) для одного фактора
б) для двух факторов
При этом свободный член определяется так
|
| |||||||||||||||||||||||||||||||||||||||||||||
|
21. |
Полные факторные планы. Середина варьирования факторов |
Xi(0)=(Ximin+Xi max)/2 | |||||||||||||||||||||||||||||||||||||||||||||
|
22. |
Интервал варьирования факторов |
| |||||||||||||||||||||||||||||||||||||||||||||
|
23. |
Соотношение натуральных факторов к их нормализованным значениям |
xi=
(Xi-
Xi0)
/ | |||||||||||||||||||||||||||||||||||||||||||||
|
24. |
Уравнение регрессии ПФП
- |
ŷ = b0+b1x1+b2x2.+ bl2х1х2 | |||||||||||||||||||||||||||||||||||||||||||||
|
25. |
Свойства матрицы планирования ПФП: 1. Симметричность относительно центра эксперимента |
∑xij=0
| |||||||||||||||||||||||||||||||||||||||||||||
|
26. |
2. Нормированность |
∑xij2=N | |||||||||||||||||||||||||||||||||||||||||||||
|
27. |
3. Ортогональность |
∑xijxuj=0 | |||||||||||||||||||||||||||||||||||||||||||||
|
28. |
Матрица базисных функций ПФП 22
| ||||||||||||||||||||||||||||||||||||||||||||||
|
29. |
Коэффициенты уравнения регрессии на основе ПФП
|
b0 = ∑yi/ N
bi = ∑xijyi/ N | |||||||||||||||||||||||||||||||||||||||||||||
|
30. |
Коэффициент при парном взаимодействии |
| |||||||||||||||||||||||||||||||||||||||||||||
|
31. |
Оценка дисперсии коэффициентов регрессии |
S2( | |||||||||||||||||||||||||||||||||||||||||||||
|
32. |
S2(y) - оценка дисперсии, характеризующая ошибку эксперимента |
| |||||||||||||||||||||||||||||||||||||||||||||
|
33. |
Оценка значимости коэффициентов регрессии |
| |||||||||||||||||||||||||||||||||||||||||||||
|
34. |
Адекватность модели
|
S2ад = Sад / fад
Fрасч. = S2ад / S2(y)
fад = N – р | |||||||||||||||||||||||||||||||||||||||||||||
|
35. |
Уравнение регрессии для В-планов второго порядка двух факторов |
yi
= b0
+ b1x1
+
b2x2
+
b11x21
+
b22x22
+
b12x1x2
| |||||||||||||||||||||||||||||||||||||||||||||
|
36. |
Матрица В-плана N = 2k + 2k В-план для k = 2
| ||||||||||||||||||||||||||||||||||||||||||||||
|
37. |
Общее число опытов В-планов |
N = 2k + 2k
| |||||||||||||||||||||||||||||||||||||||||||||
|
38. |
Вспомогательные коэффициенты
|
| |||||||||||||||||||||||||||||||||||||||||||||
|
39. |
Вспомогательные коэффициенты a, b, c ,d |
| |||||||||||||||||||||||||||||||||||||||||||||
|
40. |
Значения коэффициентов Ti |
| |||||||||||||||||||||||||||||||||||||||||||||
|
41.
|
| ||||||||||||||||||||||||||||||||||||||||||||||
|
42. |
Вычисление коэффициентов регрессии В-планов 2-го порядка для двух факторов |
| |||||||||||||||||||||||||||||||||||||||||||||
|
43. |
Вычисление дисперсии коэффициентов уравнения регрессии для В-планов второго порядка для 2x факторов |
| |||||||||||||||||||||||||||||||||||||||||||||
|
44. |
Время работы первого исполнителя
( |
| |||||||||||||||||||||||||||||||||||||||||||||
|
45. |
Время работы второго исполнителя
|
| |||||||||||||||||||||||||||||||||||||||||||||
|
46. |
Критерий эффективности (Z) имеет вид |
| |||||||||||||||||||||||||||||||||||||||||||||
|
47. |
Математическая модель |
| |||||||||||||||||||||||||||||||||||||||||||||
|
№ п/п |
Тип функции |
Вид функции |
Формулы для расчета коэффициентов |
|
1 |
Линейная |
у=f(x, k, b)=kx+b |
b |
|
2 |
Степенная |
y=axb прологарифмируем: lny = lna + blnx.
замена: t=ln x, A=ln a, q=ln y. |
|
|
3 |
Показательная |
y=f (x, a, k)= a exp (kx)=aekx
прологарифмируем: ln y=ln a + kx,
замена: ln y = q, ln a = A,
получаем: q(x) = kx+A |
|
|
4 |
Дробнолинейная |
перепишем в
|
|
|
5 |
Дробнорациона- льная |
=
a
+
замена:
получаем:
|
|
|
6 |
Логарифмичес- кая |
замена:
получаем:
|
|
|
7 |
Гипербола |
замена:
получаем:
|
|
|
8 |
Квадратичная функция |
y
= f (x, a, b, c) = ax |
М
М
М
М |


 =
=

 =
=
 ∑
∑ 2
2




 =
0,1
=
0,1
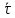















 i=
Ximax–
Xi0=
Xi0
-
Ximin
i=
Ximax–
Xi0=
Xi0
-
Ximin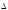 i
i
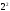

 )
= S2(y)
/ N
)
= S2(y)
/ N


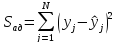














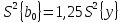
 )
)
 )
)

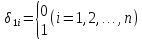




 (
( )
)



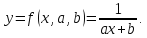



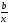
 ,
, ,
,











 + bx + c
+ bx + c М
М





 =
=
 ,Мy
=
,Мy
=
 ,М
,М =
=
 ,
, =
=
 ,М
,М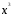 =
=
 ,М
,М =
=
