
- •Программа подготовки к экзамену по математике за II семестр для студентов сокращенной заочной формы обучения
- •Часть I
- •Контрольное домашнее задание №3 для студентов сокращенной заочной формы обучения
- •Программа подготовки к экзамену по математике
- •Тема. Элементы математической статистики.
- •Тема. Применение математических методов для обоснования решения.
- •Тема. Обоснования решения в условиях неопределенности и риска.
- •Контрольное домашнее задание №4 для студентов сокращенной заочной формы обучения
- •Типовые задачи в экзаменационных билетах.
- •Вопросы в билетах экзамена за 3 и 4 семестр
Программа подготовки к экзамену по математике за II семестр для студентов сокращенной заочной формы обучения
Часть I
Тема: "Неопределенный интеграл"
1. Первообразная: определение, примеры нахождения первообразной.
2. Неопределенный интеграл и его основные свойства.
3. Способы вычисления неопределенного интеграла: непосредственное интегрирование, замена переменной,
интегрирование по частям.
Тема: " ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ"
4. Задачи, приводящие к понятию определенный интеграл: определение площади криволинейной трапеции; вычисление пути, пройденного точкой при неравномерном движении.
5. Определенный интеграл: определение; интегральная сумма и общий порядок ее составления; геометрический смысл определенного интеграла от положительной и отрицательной функции; механический смысл определенного интеграла.
6. Основные свойства определенного интеграла: интеграл с совпадающими пределами; перестановка пределов интегрирования; разбиение интервала интегрирования.
7. Численные методы вычисления определенного интеграла: формула трапеций.
8. Производная от интеграла по верхнему пределу.
9. Формула Ньютона - Лейбница: вывод формулы, смысл результата.
10. Замена переменной в определенном интеграле: вывод формулы.
11. Интегрирование по частям при вычислении определенного интеграла: условие применения метода интегрирование по частям; основные рекомендации.
12. Геометрическое приложение определенного интеграла: вычисление площади параболической трапеции;
вычисление длин дуг; вычисление объема и поверхности тел вращения.
13.Несобственный интеграл первого рода: возможные варианты, физический смысл результата, практический пример вычисления несобственного интеграла от нечетной функции.
Тема: "ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ"
1.Дифференциальное уравнение: определение, порядок дифференциального уравнения, решение уравнения, общее и частное решение.
2. Общий метод решения дифференциального уравнение первого порядка с разделяющимися переменными.
3. Линейное дифференциальное уравнение первого порядка: определение, метод решения однородного дифференциального уравнения.
4. Линейное дифференциальное уравнение первого порядка: определение, метод решения неоднородного дифференциального уравнения.
5. Общий метод решения однородного линейного дифференциального уравнения второго порядка с постоянными коэффициентами.
Тема: "ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ"
27. Функции нескольких переменных. Основные понятия. Способы задания.
28. Частные производные функции нескольких переменных и их геометрический смысл.
29. Полный дифференциал функции нескольких переменных и его геометрический смысл.
30. Необходимое условие существования экстремума функции нескольких переменных.
31. Достаточное условие существования экстремума функции нескольких переменных.
32. Условный экстремум функции нескольких переменных.
Контрольное домашнее задание №3 для студентов сокращенной заочной формы обучения
Студент должен выполнит контрольную работу по варианту, буква которого совпадает
с первой буквой фамилии, и представить ее не позднее, чем за 2 недели до начала сессии.
Номера задач для соответствующего варианта указаны в таблице:
|
Первая буква фамилии |
Вариант № |
Номера задач | ||||||||
|
А, У, Ф |
1 |
1 |
11 |
21 |
31 |
41 |
51 |
61 | ||
|
Б, Т,Х |
2 |
2 |
12 |
22 |
32 |
42 |
52 |
62 | ||
|
В, С, Ц |
3 |
3 |
13 |
23 |
33 |
43 |
53 |
63 | ||
|
Г,Р, Ч |
4 |
4 |
14 |
24 |
34 |
44 |
54 |
64 | ||
|
Д, П, Ш |
5 |
5 |
15 |
25 |
35 |
45 |
55 |
65 | ||
|
Е,О, Щ |
6 |
6 |
16 |
26 |
36 |
46 |
56 |
66 | ||
|
Ё,Н, Э |
7 |
7 |
17 |
27 |
37 |
47 |
57 |
67 | ||
|
Ж, М,Ю |
8 |
8 |
18 |
28 |
38 |
48 |
58 |
68 | ||
|
З, Л, Я |
9 |
9 |
19 |
29 |
39 |
49 |
59 |
69 | ||
|
И,Й,К |
10 |
10 |
20 |
30 |
40 |
50 |
60 |
70 | ||
Задача №1. Вариант №1…10. Вычислить указанные пределы, используя правило Лопиталя:
1.

 6.
6.
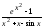
2.

 7.
7.

3.

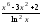 8.
8.

4.

 9.
9.

5.

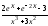 10.
10.

Задача №2. Вариант №11…20. Вычислить неопределенный интеграл методом непосредственного интегрирования:
11.
 .12.
.12. .13.
.13. . 14.
. 14.

15. 16.
16. 17.
17.
 18.
18.
19.
 20.
20.
Задача №3. Вариант №21…30. Вычислить неопределенный интеграл любым методом:
21.
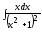 . 22.
. 22.
 23.
23.
 24.
24.
 25.
25.

26.
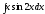 27.
27.
 28.
28.
 29.
29.
 30.
30.

Задача
№4. Вариант 31… 40. Вычислить площадь,
ограниченную линиями
 и
и .
.
31.
 ;
; . 36.
. 36. ;
; .
.
32.
 ;
; . 37.
. 37. ;
; .
.
33.
 ;
; . 38.
. 38. ;
;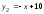 .
.
34.
 ;
; . 39.
. 39. ;
; .
.
35.
 ;
; . 40.
. 40. ;
; .
.
Задача
№5. Вариант 41… 50. Используя
формулу трапеций, вычислить площадь
параболического треугольника,
образованного параболой
 ,
осьюОх
и прямыми х=а
и х=b,
разбивая отрезок
,
осьюОх
и прямыми х=а
и х=b,
разбивая отрезок на 5 частей. Расчеты выполнить с округлением
до второго знака.
на 5 частей. Расчеты выполнить с округлением
до второго знака.
41. k= 0,5; a=0; b=5. 45. k= 0,9; a=0; b=5. 49. k= 2; a=0; b=5.
42. k= 0,6; a=0; b=5. 46. k= 1,1; a=0; b=5. 50. k= 1; a=0; b=10.
43. k= 0,7; a=0; b=5. 47. k= 1,2; a=0; b=5.
44. k= 0,8; a=0; b=5. 48. k= 1,5; a=0; b=5.
Задача №6. Вариант 51… 60. Вычислить объем тела, полученного от вращения вокруг оси Ох фигуры, ограниченной линиями у, х1, х2 и осью Ох.
|
Вариант |
у |
х1 |
х2 |
Вариант |
у |
х1 |
х2 |
|
51 |
y =6-2х |
0 |
3 |
56 |
y =3-0,5х |
2 |
5 |
|
52 |
y =6-2х |
1 |
3 |
57 |
y =3-1,5х |
0 |
1,5 |
|
53 |
y =4-х |
1 |
3 |
58 |
y =5-1,5х |
1 |
3 |
|
54 |
y =4-1,5х |
1 |
2 |
59 |
y =5-х |
1 |
4 |
|
55 |
y =5-0,5х |
2 |
10 |
60 |
y =4-0,5х |
3 |
5 |
Задача №7. Вариант 61… 70. Записать частную производную заданной функции
|
Вариант |
Функция |
Записать |
Вариант |
Функция |
Записать |
|
61 |
|
|
66 |
|
|
|
62 |
|
|
67 |
|
|
|
63 |
|
|
68 |
|
|
|
64 |
|
|
69 |
|
|
|
65 |
|
|
70 |
|
|
