
- •МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ТЕМАМ ПРОГРАММЫ
- •Тема 1. Основные понятия
- •Тема 3. Напряженное и деформированное состояние
- •Тема 4. Геометрические характеристики плоских сечений
- •Тема 5. Сдвиг. Напряжения и деформации при сдвиге
- •Тема 6. Кручение. Напряжения и деформации при кручении
- •Тема 7. Изгиб. Расчеты на прочность при изгибе
- •Тема 9. Статически неопределимые системы при изгибе
- •Тема 10. Сложное сопротивление
- •Тема 11. Устойчивость продольно сжатых стержней
- •Тема 12. Динамическое действие нагрузки
- •Тема 13. Явление усталости материалов
- •КОНТРОЛЬНЫЕ РАБОТЫ
- •ЗАДАЧА № 1. РАСЧЕТ СТЕРЖНЯ
- •Пример решения задачи № 1
- •ЗАДАЧА № 2. РАСЧЕТ НАПРЯЖЕННОГО СОСТОЯНИЯ
- •Пример решения задачи № 3
- •ЗАДАЧА № 4. РАСЧЕТ ЗАКЛЕПОЧНОГО СОЕДИНЕНИЯ
- •Пример решения задачи № 4
- •ЗАДАЧА № 5. КРУЧЕНИЕ ВАЛА КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
- •Пример решения задачи № 5
- •ЗАДАЧА № 6. РАСЧЕТ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ БАЛОК
- •Пример решения задачи № 6
- •ЗАДАЧА № 7. ПОСТРОЕНИЕ ЭПЮР ДЛЯ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ РАМ
- •Пример решения задачи № 7
- •Продолжение таблицы 9, а
- •Пример решения задачи № 8
- •ЗАДАЧА № 9. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ БАЛКИ
- •Пример решения задачи № 9
- •ЗАДАЧА № 10. ВНЕЦЕНТРЕННОЕ СЖАТИЕ СТЕРЖНЯ
- •Пример решения задачи № 10
- •ЗАДАЧА № 11. ПРОДОЛЬНЫЙ ИЗГИБ СТЕРЖНЯ
- •Методические указания к задаче № 11
- •ЗАДАЧА № 12. РАСЧЕТ БАЛКИ НА УДАРНУЮ НАГРУЗКУ
- •Пример решения задачи № 12
- •ЗАДАЧА № 13. ОПРЕДЕЛЕНИЕ ПРЕДЕЛЬНОЙ НАГРУЗКИ
- •Продолжение таблицы 15
- •Пример решения задачи № 13
- •ВОПРОСЫ К ЗАЧЕТУ И ЭКЗАМЕНУ
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК
36
Ближайшее из сортамента значение момента сопротивления составляет 289 см3, оно соответствует двутавру № 24, этот двутавр и следует использовать для балки.
В балке на двух опорах Мmax = 22 кН м, Qmax = 22 кН.
Требуемый момент сопротивления из условия прочности по нормальным
напряжениям |
|
Wx ≥ |
M max |
= |
22 103 |
=1,83 10−3 |
м3. |
Момент |
сопротивления |
||||||||||||||||
|
[σ] |
12 106 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
прямоугольного сечения Wx |
= |
b h2 |
, т. к. |
b = |
2 |
h , то |
Wx = |
2h3 |
. Требуемая высота |
||||||||||||||||
6 |
3 |
18 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
балки составит: |
h = 3 18Wx |
|
=0,254 м. Округляем до четного числа и получаем h |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
= 0,26 м. Ширина балки составит b = 0,18 м. |
|
|
|
|
|
|
|||||||||||||||||||
|
Проверим балку с выбранными размерами поперечного сечения по |
||||||||||||||||||||||||
условию |
|
Qmax |
|
|
|
прочности |
|
|
|
по |
|
касательным |
|
напряжениям: |
|||||||||||
τmax = |
3 |
|
|
|
|
= |
3 |
|
22 103 |
|
≈ 0,71 МПа, |
что меньше допустимых напряжений |
|||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
2 |
|
b h |
2 |
0,26 0,18 |
|||||||||||||||||||||
[τ]= 1,5 МПа.
В том случае, если условие прочности по касательным напряжениям не выполняется, то размеры поперечного сечения следует увеличить.
ЗАДАЧА № 7. ПОСТРОЕНИЕ ЭПЮР ДЛЯ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ РАМ
Требуется: для заданной схемы статически определимой рамы построить эпюры внутренних силовых факторов (Nz, Qу, Mх).
Условия задания:
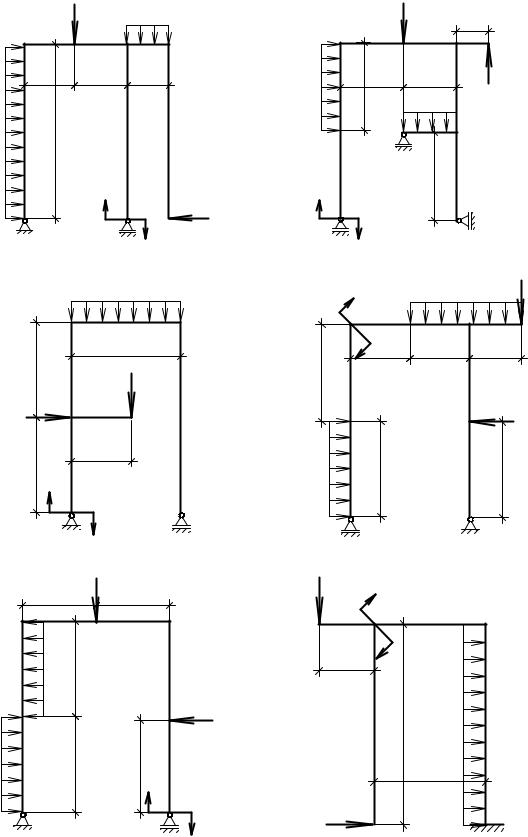
Рама загружена силами (Р1 и Р2), моментом (М) и равномерно распределенной нагрузкой (q). Расчетные схемы представлены на рис. 24, числовые данные в табл. 7.
Последовательность выполнения задания:
1.Вычертить расчетную схему рамы с заданными нагрузками. Проставить числовые значения размеров и нагрузок. Изобразить реакции и вычислить их величину.
2.Построить эпюры Nz, Qу, Mх на каждом участке. Эпюры строят на контуре рамы. Контур рамы для построения каждой эпюры следует чертить заново в том же масштабе, что и расчетную схему. Контур рамы выделяют утолщенной линией. На всех эпюрах проставить числовые значения Nz, Qу, Mх с указанием размерности.
|
|
P1 |
q |
|
|
|
|
|
a |
a |
c |
q |
2b |
|
|
|
|
M |
P2 |
|
|
|
|
|
|
Схема 1 |
|
q
2a
b
P1
P2 2a/3
b
M
Схема 3
a P1 |
a |
q
b
P2
q
b |
b |
M
Схема 5
37
P1 |
|
c |
a |
a |
P2 |
q |
q |
|
b |
|
|
|
b |
|
M |
|
|
Схема 2 |
|
|
M |
q |
P2 |
|
|
|
a |
a |
c |
b |
|
|
|
|
P1 |
q |
|
b |
b |
|
|
Схема 4 |
|
|
P1 |
M |
|
|
|
|
c |
|
|
|
2b |
q |
|
|
|
|
2a |
|
P2 |
|
|
|
Схема 6 |
|
Рис. 24. Расчетные схемы к задаче № 7
38
|
P2 |
|
a |
|
a |
b |
|
|
P1 |
|
M |
q |
|
|
b |
b |
q |
|
|
|
|
|
c |
Схема 7 |
|
|
|
q |
P2 |
b |
P1 |
|
|
|
|
|
a |
|
b |
2a |
|
|
|
P2 |
|
Схема 9 |
|
|
a |
P2 |
|
|
|
q |
|
a |
b b |
||
|
|
P1 |
|
|
q |
|
b |
|
|
M |
|
|
|
Схема 8 |
q
|
2a |
P2 |
|
b |
q |
q |
|
|
|
|
|
|
|
M |
b |
b |
c |
Схема 0
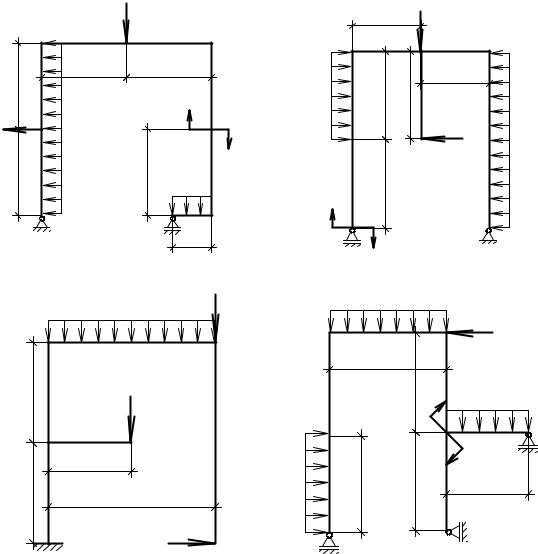
Рис. 24. Расчетные схемы к задаче № 7 (окончание)
Таблица 7
Числовые данные к задаче № 7
№ |
№ |
Р1, кН |
Р2, кН |
М, |
q, |
№ |
а, м |
b, м |
с, м |
схемы |
кН м |
кН/м |
|||||||
0 |
00 |
26 |
34 |
24 |
12 |
000 |
3,0 |
4,0 |
1,0 |
1 |
10 |
28 |
32 |
26 |
14 |
100 |
3,2 |
3,8 |
1,0 |
2 |
20 |
30 |
30 |
28 |
16 |
200 |
3,4 |
3,6 |
1,0 |
3 |
30 |
32 |
28 |
30 |
18 |
300 |
2,4 |
3,4 |
2,0 |
4 |
40 |
34 |
26 |
32 |
20 |
400 |
2,6 |
4,2 |
1,6 |
5 |
50 |
36 |
24 |
34 |
22 |
500 |
2,8 |
4,4 |
1,4 |
6 |
60 |
38 |
32 |
36 |
24 |
600 |
3,0 |
4,6 |
1,3 |
7 |
70 |
40 |
30 |
38 |
16 |
700 |
3,2 |
4,8 |
1,2 |
8 |
80 |
38 |
28 |
40 |
18 |
800 |
3,4 |
5,0 |
1,1 |
9 |
90 |
36 |
26 |
40 |
10 |
900 |
3,6 |
4,5 |
1,0 |
39
Пример решения задачи № 7
Для продольных сил (Nz) и поперечных сил (Qу) сохраняют принятые ранее правила знаков. Ординаты эпюр Nz и Qу откладывают перпендикулярно к оси элементов рамы в произвольную сторону, но обязательно указывается знак.
Для изгибающих моментов специального правила знаков нет, а при вычислении момента в любом сечении знак принимается произвольно. Но результат вычислений всегда откладывается со стороны сжатого волокна элемента рамы.
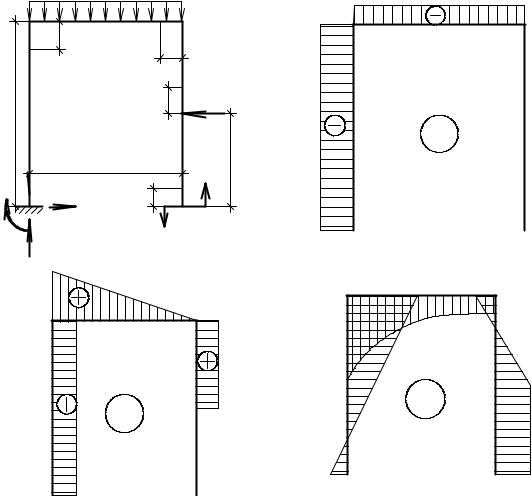
Рассмотрим жестко защемленную плоскую раму (рис. 25, а). В жесткой заделке возникают три реакции, но строить эпюры внутренних силовых факторов для такого типа рамы можно без вычисления реакций в заделке.
Рама имеет 4 участка. Построение эпюры Nz.
Первый участок 0 ≤ z1 ≤ 3 м.
N1 = 0.
Второй участок 0 ≤ z2 ≤ 3 м.
N2 = 0.
Третий участок 0 ≤ z3 ≤ 4 м.
N3 = − Р = − 20 кН (сжатие «−»).
Четвертый участок 0 ≤ z4 ≤ 6 м.
N4 = − q 4 = − 40 кН (сжатие «−»).
Эпюра продольных сил показана на рис. 25, б. Из эпюры видно, что вертикальная реакция в защемлении RА = 40 кН и направлена вверх, вызывая сжатие в стойке рамы.
Построение эпюры Qу.
Первый участок 0 ≤ z1 ≤ 3 м.
Q1 = 0.
Второй участок 0 ≤ z2 ≤ 3 м.
Q2 = Р = 20 кН (знак «+», т. к. сила Р стремится повернуть сечение по ходу часовой стрелки).
Третий участок 0 ≤ z3 ≤ 4 м.
Q3 = q z3. При z3 = 0, Q3 = 0, z3 = 4 м, Q3 = 40 кН.
Четвертый участок 0 ≤ z4 ≤ 6 м.
Q4 = − Р = − 20 кН.
Эпюра поперечных сил показана на рис. 25, в. Из эпюры видно, что горизонтальная реакция защемления НА = 20 кН и направлена вправо.
Построение эпюры Мх.
Первый участок 0 ≤ z1 ≤ 3 м.
М1 = М = 40 кН м (сжатым является правое волокно в сечении, поэтому ордината отложена вправо от оси стойки).
Второй участок 0 ≤ z2 ≤ 3 м.
М2 = М − Р z2. При z2 = 3 м М2 = − 20 кН м.
Третий участок 0 ≤ z3 ≤ 4 м.
40
М3 = М – Р 3 − q z3 z3/2. При z3 = 0, М3 = − 20 кН м, z3 = 4 м,
М3 = − 100 кН м (сжаты нижние волокна). Эпюра изгибающих моментов имеет вид квадратичной параболы.
Четвертый участок 0 ≤ z4 ≤ 6 м.
Вверхнем левом углу стойки М4 = М − Р 3 − q 4 2 = − 100 кН м.
Вопоре А М4 = М + Р 3 − q 4 2 = 20 кН м.
Эпюра изгибающих моментов представлена на рис. 25, г. Реактивный момент в защемлении МА = 20 кН м.
Проверка правильности определения реакций из уравнений статики.
∑X = 0, H A − P = 20 −20 = 0 ;
∑Y = 0, RA −q 4 = 40 −10 4 = 0 ;
∑M = 0, M A + q 4 2 − P 3 − M = 20 +10 4 2 −20 3 −40 = 0 .
а)
q=10 êÍ/ì
|
|
40 |
20 |
4 |
z3 |
|
|
z |
|
||
|
2 |
P=20 êÍ |
|
6 ì |
z |
б) |
Nz |
|
4 ì |
ì |
|
|
|
||
|
3 |
|
|
|
|
|
|
H |
1 |
|
|
A |
z |
Ì=40 êÍ ì |
|
MA RA |
|
|
|
|
|
|
|
40 |
|
в) |
|
Qy |
20 |
20 |
|
|
100 |
20 |
г) |
100 |
40 |
|
||
|
Mx |
|
|
20 |
40 |
Рис. 25. Пример построения эпюр внутренних силовых факторов в жестко защемленной раме
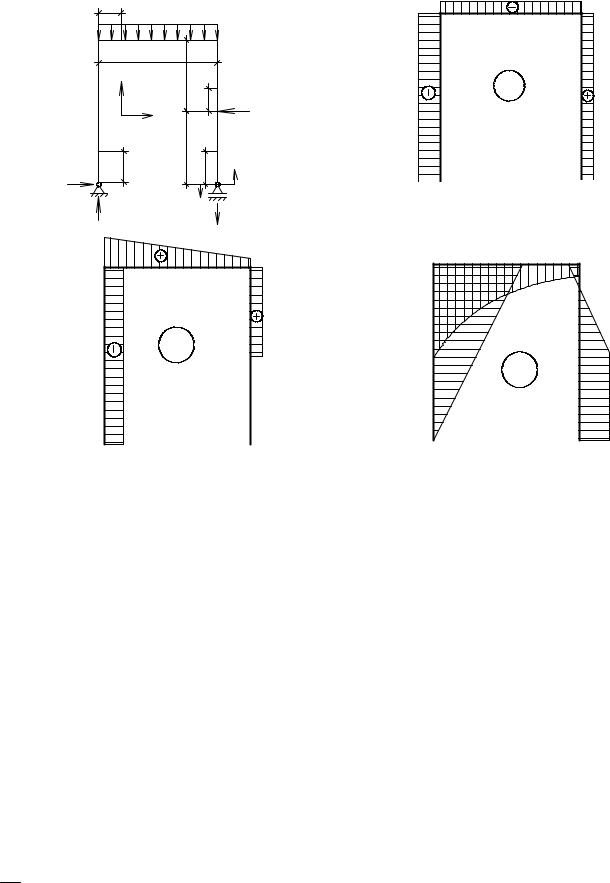
Рассмотрим раму на двух шарнирных опорах (рис. 26, а). Определим реакции в опорах рамы из уравнений статики
∑X = 0, H A − P = 0 H A = 20 кН;
41
∑M A = 0, q 4 2 − P 3 − M − RB 4 = 0 |
|
RB = −5 кН; |
∑M B = 0, RA 4 −q 4 2 − P 3 − M = 0 |
|
RA = 45 кН. |
Построение эпюры Nz. Первый участок 0 ≤ z1 ≤ 6 м. N1 = − RВ = − 45 кН (сжатие). Второй участок 0 ≤ z2 ≤ 4 м. N2 = − НА = − 20 кН (сжатие). Третий участок 0 ≤ z3 ≤ 3 м. N3 = RВ = 5 кН (растяжение). Четвертый участок 0 ≤ z4 ≤ 3 м.
N4 = RВ = 5 кН.
Эпюра продольных сил представлена на рис. 26, б. Построение эпюры Qу.
Первый участок 0 ≤ z1 ≤ 6 м.
Q1 = − НА = − 20 кН.
Второй участок 0 ≤ z2 ≤ 4 м.
Q2 = RА − q z2. При z2 = 0 Q2 = 45 кН, при z2 = 4 м Q2 = 5 кН.
Третий участок 0 ≤ z3 ≤ 3 м.
Q3 = 0.
Четвертый участок 0 ≤ z4 ≤ 3 м.
Q4 = Р = 20 кН.
Эпюра поперечных сил показана на рис. 26, в. Построение эпюры Мх.
Первый участок 0 ≤ z1 ≤ 6 м.
М1 = НА z1 (сжаты правые волокна стойки). При z1 = 6 м М1 = 120 кН м.
Второй участок 0 ≤ z2 ≤ 4 м.
М2 = НА 6 − q z2 z2/2. При z2 = 4 м М2 = − 20 кН м.
Третий участок 0 ≤ z3 ≤ 3 м.
М3 = М = 40 кН м (сжаты правые волокна стойки). Четвертый участок 0 ≤ z4 ≤ 3 м.
М4 = М − Р z4. При z4 = 3 м М4 = − 20 кН м.
Эпюра изгибающих моментов показана на рис. 26, г.
42
а)
HA
z2 |
q=10 êÍ/ì |
|
|
||
|
4 ì |
|
ó |
õ |
3 ì |
|
4 |
|
|
|
z |
|
|
3 ì |
1 |
|
3 |
z |
|
z |
A
RA
|
20 |
|
Ð=20 êÍ |
б) |
Nz |
|
|
|
M=40 êÍ ì |
|
|
B |
4540 |
5 |
RB |
20 |
|
|
|
45 |
5 |
|
|
120 |
20 |
|
|
|
|
|
20 |
в) |
Qy |
г) |
120 |
Mx |
|
|
20 |
|
|
|
|
|
20 |
|
|
|
40 |
|
|
|
|
|
Рис. 26. Пример построения эпюр внутренних силовых факторов в раме на двух шарнирных опорах
ЗАДАЧА № 8. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ БАЛКАХ
Требуется: для заданной схемы статически определимой балки определить вертикальное перемещение указанного сечения (уД или уЕ) и угол поворота сечения в одной из опор балки (θА или θВ), используя графоаналитический метод.
Условия задания:
Балка загружена силой Р и моментом М. Расчетные схемы представлены на рис. 27, числовые данные в табл. 8.
Последовательность выполнения задания:
1.Начертить расчетную схему балки с размерами и значениями внешних нагрузок.
2.Начертить грузовую эпюру Мр − эпюру изгибающих моментов от заданных внешних сил.
3.Составить единичное состояние. Начертить единичную эпюру
Mi изгибающих моментов.
43
4. Перемещения в балке определить методом перемножения эпюр. Выражения для площадей эпюр и положения центров тяжести приведены в табл. 9. Выражения интеграла Мора для различных сочетаний единичных и грузовых эпюр приведены в табл. 9 а.
|
M |
P |
B |
|
P |
|
|
M |
A |
D |
E |
|
A |
E |
|
B |
|
|
|
|
D |
|
|
|||
a |
b |
c |
|
|
a |
b |
|
c |
|
Схемы 1, 0 |
|
|
Схемы 2, 7, 9 |
|
|||
M |
D |
E |
B |
|
D |
M |
E |
B |
A |
A |
|
||||||
|
P |
|
P |
|
||||
a |
b |
|
|
a |
|
c |
||
c |
|
|
b |
|
||||
|
Схемы 3, 6, 8 |
|
|
Схемы 4, 5 |
|
|
||
|
|
Рис. 27. Расчетные схемы к задаче № 8 |
|
|
|
|||
Таблица 8
Числовые данные к задаче № 8
№ |
№ |
Р, кН |
М, |
Угол |
№ |
а, м |
b, м |
с, м |
Сечение |
схемы |
|
|
кН м |
|
|
|
|
|
|
1 |
10 |
6,0 |
4,0 |
θА |
100 |
1,2 |
1,4 |
1,4 |
Е |
2 |
20 |
8,0 |
6,0 |
θВ |
200 |
1,4 |
1,6 |
1,2 |
D |
3 |
30 |
4,0 |
8,0 |
θА |
300 |
1,6 |
1,2 |
1,8 |
Е |
4 |
40 |
10,0 |
4,0 |
θВ |
400 |
1,0 |
1,8 |
1,2 |
D |
5 |
50 |
6,0 |
10,0 |
θА |
500 |
1,2 |
1,4 |
1,6 |
Е |
6 |
60 |
8,0 |
6,0 |
θВ |
600 |
1,8 |
1,6 |
1,2 |
D |
7 |
70 |
4,0 |
8,0 |
θА |
700 |
1,4 |
1,0 |
1,6 |
Е |
8 |
80 |
10, |
4,0 |
θВ |
800 |
1,6 |
1,4 |
1,2 |
D |
9 |
90 |
6,0 |
8,0 |
θА |
900 |
1,8 |
1,2 |
1,0 |
Е |
0 |
00 |
8,0 |
6,0 |
θВ |
000 |
1,0 |
1,6 |
1,4 |
D |
|
|
|
|
|
|
|
|
|
|
|
|
44 |
|
|
|
|
|
|
|
|
|
|
|
|
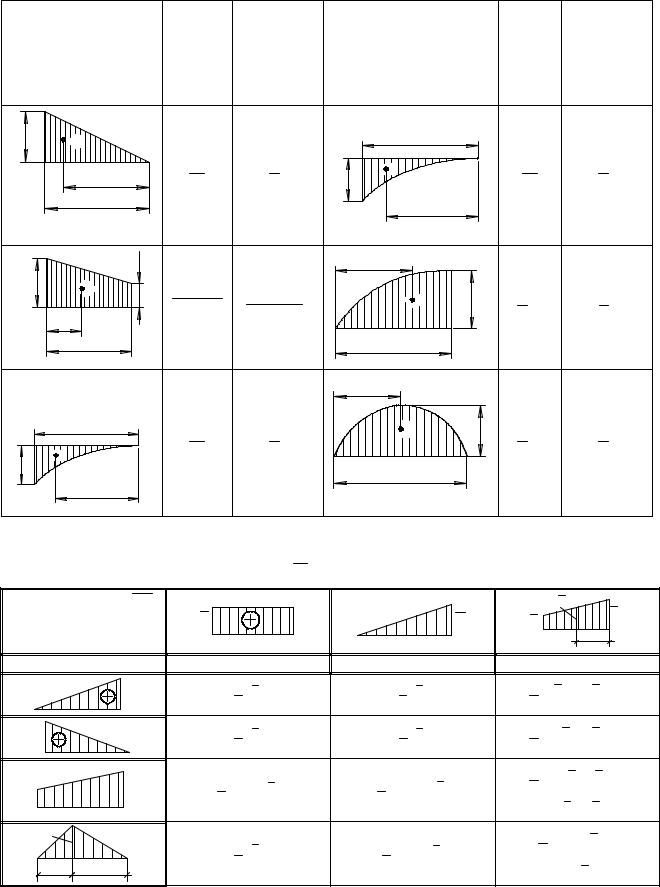
Таблица 9 |
|
|
|
Геометрические характеристики эпюр |
|
|
|||||||
|
|
|
|
|
|
с |
|
|
|
|
|
с |
Эпюра изгибающего |
Площадьω |
|
|
Координата центра тяжести z |
Эпюра изгибающего |
Площадьω |
Координата центра тяжести z |
|||||
|
момента |
|
|
|
момента |
|
||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
Кубическая парабола |
|
|
|||
h |
c |
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
zc |
hl |
|
|
2 l |
h |
|
c |
|
hl |
4 l |
|
|
l |
2 |
|
|
3 |
|
|
zc |
|
4 |
5 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
zc |
|
|
|
|
|
|
h |
(h + h0 )l |
|
|
|
|
|
|
|
||
h |
c |
h + h0 |
|
|
c |
h |
2 |
5 |
||||
|
zc |
|
2 |
|
|
3(h + h0 )l |
|
|
|
|
3 hl |
8 l |
|
|
l |
|
|
|
|
|
|
l |
|
|
|
|
Квадратичная |
|
|
|
|
|
zc |
|
|
|
|
|
|
парабола |
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
hl |
|
|
3 l |
|
|
c |
h |
2 hl |
1 l |
|
|
|
|
|
|
|
|
|
||||
h |
c |
|
3 |
|
|
4 |
|
|
l |
|
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
zc |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 9 а |
|
Выражения интеграла Мора ∫M i M p dz для различных сочетаний эпюр |
|||||||||||
|
|
ЭпюраMi |
|
|
|
|
|
|
|
|
|
h0 |
|
|
h |
|
|
|
|
|
|
h |
h1 |
h2 |
|
|
|
|
|
|
|
|
|
|
||||
Эпюра Мр |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
l/2 |
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 |
|
|
|
2 |
|
|
3 |
|
|
4 |
|
|
h |
|
|
1 |
|
|
|
1 |
|
1 |
|
|
|
|
|
2 hhl |
|
|
3 hhl |
|
6 h(h1 + 2h2 ) l |
|||
|
|
|
|
|
|
|
|
|||||
|
h |
|
|
|
1 |
|
|
|
1 |
|
1 |
|
|
|
|
|
2 hhl |
|
|
6 hhl |
|
6 h(2h1 + h2 ) l |
|||
|
|
|
|
|
|
|
|
|||||
|
|
h2 |
|
1 |
(h1 |
+ h2 )hl |
|
1 |
(h1 + 2h2 )hl |
|
1 [h1 (2h1 + h2 )+ |
|
|
h1 |
|
2 |
|
6 |
|
6 |
|
||||
|
|
|
|
|
|
|
|
+ h2 (2h2 + h1 )] l |
||||
|
|
|
|
|
|
|
|
|
|
|
||
|
h |
|
|
|
1 hhl |
|
1 (1 + α)hhl |
|
16 [(1 +β)h1 + |
|||
|
αl |
βl |
|
|
2 |
|
|
6 |
|
+ (1 + α)h2 ] hl |
||
|
|
|
|
|
|
|
|
|||||
