Истечение жидкости через отверстия и насадки

Классификация отверстий:

1. малые (геометрический напор постоянный по отверстию, то есть высота отверстия в вертикальной стенке не больше) ибольшие (геометрический напор переменный по отверстию). Отверстие любого размера в дне сосуда будет малым;

2. форма отверстия правильная, неправильная;

3. тонкостенные (толщина стенки не влияет на условия истечения ) итолстостенные (толщина стенки сказывается на условиях истечения);

4. отверстия в вертикальной, наклонной стенках и дне сосуда.

Классификация истечений:

1. при постоянном и переменном напорах;

2. из сосудов с вертикальной осью и неправильной формы;

3. свободное (чаще всего в атмосферу, уровень жидкости за отверстием не влияет на истечение), несвободное (из подтопленных или затопленных отверстий, истечение под уровень);

4. при всестороннем и неполном сжатии струи;

5. при совершенном (стенки и дно сосуда не влияют на истечение) и несовершенном сжатии струи (стенки или дно сосуда влияют на истечение, при - -расстояние от боковой стенки или дна меньше утроенного размера отверстия).

Истечение жидкости через отверстие может происходить при постоянном и переменном напоре. Если истечение жидкости через отверстие происходит в атмосферу или другую газовую среду, то такое отверстие называется незатопленным. Если же истечение идет под уровень, а не в атмосферу - затопленным.

При истечении жидкости через отверстие различают полное (а) и неполное (б) сжатие струи (рис. 49).

При прохождение через отверстие струя сжимается, и сечение ее в самом тонком месте называется сжатым сечением С - С, которое находится на расстоянии от стенки.

Площадь живого сечения в С - С:

, (157)

где - площадь струи в сжатом сечении,;

- площадь отверстия, ;

- коэффициент сжатия, (для круглого отверстия ).

а б

Рис. 49. Форма струи при истечении через отверстия.

Форма струи при истечении меняется, и этот процесс называется инверсией струи.

2.14.1. Истечение жидкости через малое отверстие в тонкой стенке

Возьмем сосуд с жидкостью и отверстием, которое работает под постоянным напором (рис. 50). Определим скорость в сеченииС - С. Для этого воспользуемся уравнением Бернулли и напишем его для сечений 0 - 0 и С - С относительно плоскости сравнения 0₁ - 0₁, проходящей через центр тяжести отверстия:

(158)

_{Принимаем скорость течения в сечении} С - С через . Давление на свободной поверхности и в сеченииС - С одинаковым и равным атмосферному ;; , тогда (158) примет вид:

(159)

Но 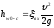, т.к. мы имеем только местные потери напора на вход потока в отверстие и уравнение (158) будет таким:

(160)

обозначим

- (полный напор)

тогда

.

Рис. 50. Истечение при постоянном напоре

Откуда скорость истечения в сжатом сечении:

; (161)

Обозначим

,

и окончательная формула для :

, (162)

где - коэффициент скорости, .

Расход жидкости:

, (163)

обозначим и

, (164)

где - коэффициент расхода (для круглых отверстий в тонкой стенке ).

Коэффициенты , ,, определяются опытным путем, их величина зависит от расположения отверстия относительно стенок сосуда, а также от числа Рейнольдса.

На графике (рис. 51) А.Д. Альтшулем построены кривые для круглого отверстия , ; .

(165)

При истечении маловязких жидкостей (вода, бензин, керосин), которое осуществляется при 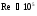, коэффициенты, ,, изменяются в небольших пределах, поэтому при расчетах принимают: , ,,.

Рис. 51. Зависимости коэффициента расхода, коэффициента скорости и коэффициента сжатия от критерия Рейнольдса