4. Проектирование плана дороги

В задании для кривых участков по значениям угла поворота α и радиуса круговой кривой R определяются основные элементы закруглений: Т – дорожный тангенс, м; Б – дорожную биссектрису, м; К – длину кривой, м; Д – домер кривой, м. Их значения определяют по таблицам или следующим формулам:

(39)

(40)

K = (41)

(42)

Для обеспечения плавного въезда в круговую кривую малого радиуса и выезда из кривой последние сопрягают с прямыми участками трассы посредствам переходных кривых. На дорогах общего пользования переходные кривые устраиваются на дорогах всех категорий с радиусом 2000 м и менее:

Радиусы круговых кривых, м	30	60	100	200	300	400	500	600 - 1000	1000 – 2000
Длина переходных кривых L, м	30	40	50	70	90	100	110	120	100

Приведённые длины переходных кривых следует рассматривать как минимально допустимые. Нормативную длину переходных кривых целесообразно увеличить в 1,5 – 2 раза, это придаст трассе дороги большую плавность и будет способствовать проезду по кривой без снижения скорости.

В практике проектирования автомобильных дорог наибольшее распространение получили переходные кривые типа клотоиды, которые характеризируются линейным законом нарастания кривизны. В качестве переходной кривой, как самостоятельного элемента трассы, применяется только начальный участок клотоиды от точки отхода от прямого участка, где r=∞, до точки на кривой, где r=R (на расстояние L от начала клотоиды).

Уравнение клотоиды имеет вид:

(43)

где r – радиус кривизны;

S – расстояние от начала клотоиды до любой точки на ней.

C – параметр клотоиды: (R – радиус круговой кривой, L – длина переходной кривой (клотоиды)).

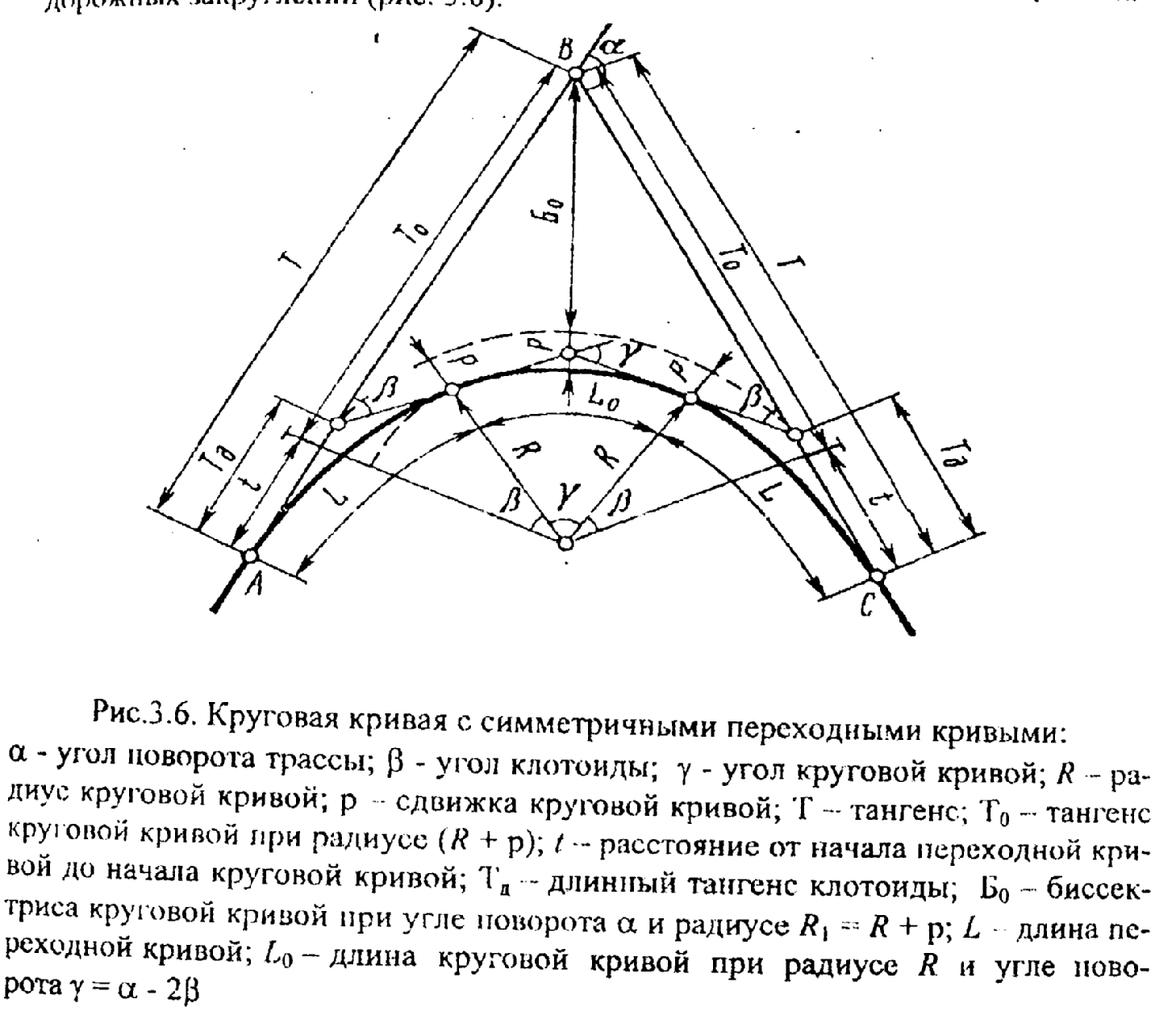
Проектирование переходной кривой по клотоиде возможно при выполне­нии условия

(44)

где α – угол поворота трассы;

β - угол между касательной переходной кривой и осью абсцисс.

(в радианах) (45)

(в градусах) (46)

Если , то рекомендуется увеличивать радиус круговой кривой.

Для определения элементов закругления с круговой вставкой между переходными кривыми необходимо определить две величины:

1. величина сдвижки (смещения) круговой кривой в ее внутреннюю сторону после разбивки переходной кривой

(47)

где у₀ - конечная ордината переходной кривой.

Если сдвижка , то смещением круговой кривой можно пренеб­речь.

В конце переходной кривой, т.е. в точке сопряжения ее с круговой кривой координаты клотоиды определяются:

(48)

(49)

2. расстояние от начала переходной кривой до начала круговой кривой:

(50)

Существует метод определения ρ и t по таблицам (Ксенодохов В.И. Таблицы для клотоидного проектирования и разбивки плана и профиля автомобильных дорог. М.,1981):

• вычислить угол переходной кривой , затем по аргументунайти по таблицам параметры клотоиды (ρ иt) при R=100 м;

• вычислить отношение фактического радиуса круговой кривой к табличному R_ф/R_табл.;

• определить фактические значения элементов переходной кривой (ρ и t) умножением табличных величин на отношение R_ф/R_табл:

(51)

(52)

Основные геометрические элементы горизонтальных закруглений с переходными клотоидными кривыми:

Радиус (53)

Тангенс (54)

где (55)

Биссектриса (56)

Длина всей кривой (57)

Домер (58)

где L – длина переходной кривой, м;

L₀ – длина круговой кривой при радиусе R₀ и угле поворота , м;

(59)

После определения всех элементов круговых и переходных кривых заполняют ведомость углов поворота, прямых и кривых.

Пикетажное положение главных точек закругления определяют согласно формулам:

(60)

(61)

(62)

(63)

Проверку выполненных расчетов проводят по формулам:

(64)

(65)

(66)

где - сумма длин прямых вставок, м;

- сумма длин всех прямых участков трассы между вершинами углов, м;

- сумма длин кривых участков трассы, м;

- сумма домеров, м;

- сумма левых углов поворота;

- сумма правых углов поворота;

- азимут начального направления трассы;

- азимут конечного направления трассы.