
23-11-2015_20-04-52 / для студентов гл.7-10
.pdf794. Найдите объём треугольной пирамиды SABC, если:
а) угол САВ равен 90°, ВС = c, угол АВС равен φ и каждое боковое ребро составляет с плоскостью основания угол θ; б) АВ = 12 см, ВС = СА = 10 см и двугранные углы при основании равны 45°;
в) боковые рёбра попарно перпендикулярны и имеют длины а, b и с.
795.Основанием пирамиды является прямоугольный треугольник с катетами a и b. Каждое её боковое ребро наклонено к плоскости основания под углом φ. Найдите объём пирамиды.
796.Объём правильной пирамиды MABC равен 2 см³. Основание АВС пирамиды – правильный треугольник со стороной 3 см. Найдите угол наклона к основанию бокового ребра МА.
см³. Основание АВС пирамиды – правильный треугольник со стороной 3 см. Найдите угол наклона к основанию бокового ребра МА.
797.Объясните, какой должна быть длина ребра правильного тетраэдра, чтобы его площадь полной поверхности была равна 4 см2.
798.Основаниями усечённой пирамиды являются правильные треугольники со сторонами 5 см и 3 см. Одно из боковых рёбер перпендикулярно к плоскости основания и равно 1 см. Найдите площадь боковой поверхности усечённой пирамиды.
799.В правильной четырёхугольной усечённой пирамиде стороны оснований равны 24 см и 8 см, высота – 15 см. Вычислите площадь полной поверхности пирамиды.
800.В правильной четырёхугольной усечённой пирамиде площади оснований равны 25 см² и 9 см², боковое ребро образует с плоскостью нижнего основания угол 45°. Вычислите площадь боковой поверхности пирамиды.
801.Найдите объём правильной треугольной пирамиды с боковым ребром l, если:
а) боковое ребро составляет с плоскостью основания угол φ; б) боковое ребро составляет с прилежащей стороной основания угол α; в) плоский угол при вершине равен β.
802.В правильной треугольной пирамиде плоский угол при вершине равен φ, а сторона основания равна а. Найдите объём пирамиды.
803.Найдите объём правильной четырёхугольной пирамиды, если:
а) её высота равна H, а двугранный угол при основании равен β;
б) сторона основания равна m, а плоский угол при вершине равен α.
804.Боковое ребро правильной четырёхугольной пирамиды равно m и составляет с плоскостью основания угол φ. Найдите объём пирамиды.
805.Найдите объём пирамиды и площадь боковой поверхности правильной шестиугольной пирамиды, если её боковое ребро равно 13 см, а диаметр круга, вписанного в основание, равен 6 см.
§3. Правильные многогранники. Симметрия в пространстве.
. Правильные многогранники.
Определение. Выпуклый многогранник называется правильным, если все его грани – равные правильные многоугольники и в каждой его вершине сходится одно и то же число рёбер.
Достаточно легко доказать, что правильных многогранников существует всего 5: правильный тетраэдр, правильный гексаэдр, правильный октаэдр, правильный икосаэдр,
31
правильный додекаэдр. Этот поразительный факт дал повод древним мыслителям соотнести правильные многогранники и первоэлементы бытия.
Есть много интересных приложений теории многогранников. Одним из выдающихся результатов в данной области является теорема Эйлера, справедливая не только для правильных, но и для всех выпуклых многогранников.
Теорема: для выпуклых многогранников справедливо соотношение: Г + В – Р = 2, где В – число вершин, Г – число граней, Р – число ребер.
Название |
Количество |
Количество |
Количество |
Г + В – Р |
Первоэлемент |
многогранника |
граней (Г) |
вершин (В) |
рёбер (Р) |
|
бытия |
тетраэдр |
4 |
4 |
6 |
2 |
Огонь |
гексаэдр |
6 |
8 |
12 |
2 |
Земля |
октаэдр |
8 |
6 |
12 |
2 |
Вода |
икосаэдр |
20 |
12 |
30 |
2 |
Воздух |
додекаэдр |
12 |
20 |
30 |
2 |
Вселенная |
четырехугольная |
5 |
5 |
8 |
2 |
|
пирамида |
|
||||
|
|
|
|
|
|
n – угольная |
n + 1 |
n + 1 |
2 n |
2 |
|
пирамида |
|
||||
|
|
|
|
|
|
треугольная |
5 |
6 |
9 |
2 |
|
призма |
|
||||
|
|
|
|
|
|
n – угольная |
n + 2 |
2n |
3n |
2 |
|
призма |
|
||||
|
|
|
|
|
Правильные многогранники обладают многими интересными свойствами. Одним из самых поразительных свойств является их двойственность: если соединить отрезками центры граней правильного гексаэдра (куба), то получится правильный октаэдр; и, наоборот, если соединить отрезками центры граней правильного октаэдра, то получится куб. Аналогично, двойственны правильные икосаэдр и додекаэдр. Правильный тетраэдр двойственен сам себе, т.е. если соединить отрезками центры граней правильного тетраэдра, то снова получится правильный тетраэдр.
. Симметрия в пространстве.
Определение. Точки А и В называются симметричными относительно точки О
(центр симметрии), если О – середина отрезка АВ. Точка О считается симметричной самой себе.
Определение. Точки А и В называются симметричными относительно прямой а
(ось симметрии), если прямая а проходит через середину отрезка АВ и перпендикулярна этому отрезку. Каждая точка прямой а считается симметричной самой себе.
Определение. Точки А и В называются симметричными относительно плоскости
β (плоскости симметрии), если плоскость β проходит через середину отрезка АВ и перпендикулярна этому отрезку. Каждая точка плоскости β считается симметричной самой себе.
Определение. Точка (прямая, плоскость) называются центром (осью, плоскостью) симметрии фигуры, если каждая точка фигуры симметрична относительно неё некоторой точке той же фигуры.
Если фигура имеет центр (ось, плоскость) симметрии, то говорят, что она обладает центральной (осевой, зеркальной) симметрией. Центр, ось и плоскости симметрии многогранника называются элементами симметрии этого многогранника.
32

Пример. Правильный тетраэдр:
–не имеет центра симметрии;
–имеет три оси симметрии – прямые, проходящие через середины двух противоположных рёбер;
- имеет шесть плоскостей симметрии – плоскости, проходящие через ребро перпендикулярно противоположному (скрещивающемуся с первым) ребру тетраэдра.
Вопросы и задачи
806.Сколько центров симметрии имеет: а) параллелепипед;
б) правильная треугольная призма; в) двугранный угол; г) отрезок; д) шар?
807.Сколько осей симметрии имеет:
а) отрезок; б) правильный треугольник; в) круг; г) шар?
808. Сколько плоскостей симметрии имеет:
а) правильная четырёхугольная призма, отличная от куба; б) правильная четырёхугольная пирамида; в) правильная треугольная пирамида; г) шар?
809. Сколько и каких элементов симметрии имеют правильные многогранники: а) правильный тетраэдр; б) правильный гексаэдр; в) правильный октаэдр; г) правильный икосаэдр;
д) правильный додекаэдр?
33
 Глава 9. Фигуры (тела) вращения.
Глава 9. Фигуры (тела) вращения.
§ 1. Цилиндр (рассматриваем только прямой круговой цилиндр).
. Цилиндр. Основные понятия.
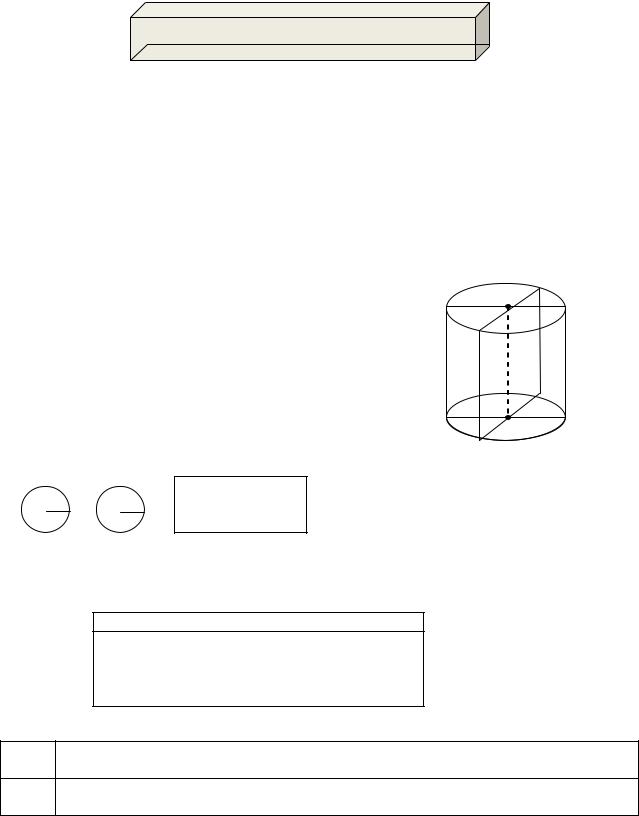
Определение. Цилиндром называется геометрическая фигура, полученная вращением прямоугольника вокруг одной из его сторон. Сторона, относительно которой происходит вращение – ось цилиндра, противоположная ей сторона называется образующей (образует при вращении боковую поверхность цилиндра), две другие – радиусы нижнего и верхнего оснований цилиндра.
ОО1 – ось цилиндра,
АА1 = ВВ1 =…= l – образующие цилиндра,
ОА = ОВ =…= ОА1 = ОВ1 = R – радиусы нижнего и верхнего оснований.
В прямом круговом цилиндре ось, образующие и высота численно равны. Осевое сечение цилиндра – прямоугольник (например, АВВ1А1).
Сечение цилиндра плоскостью, параллельной |
||
основаниям, является кругом, равным |
|
|
основаниям. |
2πR |
|
|
|
|
R |
R |
H=l |
B1
O1
A1
B
O
A
Развёртка поверхности цилиндра состоит из двух кругов (верхнее и нижнее основание) и прямоугольника (боковая поверхность).
. Объём и площадь поверхности цилиндра.
Цилиндр
Sосн = π R2
Sбок = 2πRH
Sпов = 2π R2 +2πRH = 2πR(R+H)
V = π R2H
Здесь R – радиус основания, H – высота.
!Около цилиндра всегда можно описать шар. Центр шара лежит на середине высоты.
!В цилиндр можно вписать шар, если диаметр основания цилиндра равен его высоте.
34

Вопросы и задачи
810.Высота и радиус основания цилиндра уменьшены в 2 раза. Укажите, как изменился его объём. Как изменится объём цилиндра, если все его линейные размеры увеличить в 3 раза?
811.Объём цилиндра хотят удвоить, не меняя основания цилиндра. Укажите, как следует изменить высоту.
812.Объём цилиндра хотят удвоить, не меняя его высоту. Укажите, как следует изменить радиус его основания.
813.Радиус основания цилиндра 2 см, а его высота 3 см. Выясните, больше его объём 37 см³ или меньше.
814.Радиус основания цилиндра 1 см, а его высота 2 см. Укажите длину ребра равновеликого ему (имеющего с ним равный объём) куба
815.Хозяйка планирует перелить суп из полной кастрюли с радиусом основания 10 см и высотой 15 см в кастрюлю с радиусом основания 9 см и высотой 18 см. Получится ли у неё это?
816.Найдите площадь полной поверхности цилиндра:
а) радиус основания которого равен 3, а высота – 2; б) радиус основания которого равен 2, а площадь осевого сечения – 4;
в) радиус основания которого равен 2, а диагональ осевого сечения наклонена к плоскости основания под углом 450.
817.Высота цилиндра 2 см, а радиус его основания 1 см. Объясните больше или меньше 18 см2 полная поверхность цилиндра.
818.Длина отрезка, соединяющего центр верхнего основания цилиндра с точкой нижней окружности, 10 см, а длина отрезка, соединяющего центры оснований, 8 см. Найдите объём цилиндра.
819.Отрезок, соединяющий центр верхнего основания цилиндра с точкой нижней окружности, наклонён к основанию цилиндра под углом 30°. Радиус основания 2 см. Найдите объём цилиндра.
820.Осевое сечение цилиндра – квадрат, площадь которого 4 см². Найдите объём цилиндра.
821.Бетонные кольца для колодцев имеют высоту 1 м, внешний диаметр 1 м и толщину стенок 0,1 м. Найдите объём бетона, необходимый для изготовления такого кольца.
822.Сколько понадобится краски, чтобы покрасить бак цилиндрической формы с диаметром основания 1,5 м и высотой 3 м, если на один квадратный метр расходуется 200 г краски?
823.Сколько квадратных метров жести пойдёт на изготовление трубы длиной 4 м и диаметром 20 см, если на швы необходимо добавить 2,5% площади её боковой поверхности?
824.Высота цилиндра на 12 см больше его радиуса, площадь полной поверхности равна 288π см². Найдите радиус основания и высоту цилиндра.
35
825.Диаметр основания цилиндра равен 1 м, высота цилиндра равна длине окружности основания. Найдите площадь боковой поверхности цилиндра.
826.Площадь боковой поверхности цилиндра равна S. Найдите площадь осевого сечения цилиндра.
827.Площадь основания цилиндра равна Q, а площадь его осевого сечения равна S. Найдите объём цилиндра.
828.Цилиндр получен вращением квадрата со стороной а вокруг одной из его сторон. Найдите площадь:
а) осевого сечения цилиндра; б) боковой поверхности цилиндра;
в) полной поверхности цилиндра.
829.Сторона основания правильной треугольной призмы равна радиусу основания цилиндра, а её высота в 3 раза больше высоты цилиндра. Сравните объёмы цилиндра и призмы.
830.Куб с ребром 1 вписан в цилиндр. Сравните площади полной поверхности куба и цилиндра.
831.Найдите отношение объёмов цилиндра и куба, если:
а) цилиндр описан около куба; б) цилиндр вписан в куб.
832.Определите, какой высоты должен быть цилиндр, чтобы площадь его боковой поверхности была втрое больше площади его основания.
833.Прямоугольник со сторонами a и b (a < b) вращается сначала вокруг одной из сторон, а затем вокруг другой. Сравните:
а) площади боковых поверхностей цилиндров; б) площади их полной поверхности.
834. Площадь боковой поверхности цилиндра равна 2π. Укажите:
а) есть ли среди таких цилиндров цилиндр с наибольшим объёмом; б) есть ли среди таких цилиндров цилиндр с наименьшим объёмом;
в) каким будет радиус такого цилиндра, если ещё известно, что его объём равен π.
835. Высота цилиндра равна 1. Объясните:
а) может ли площадь его полной поверхности быть равна 4π; б) какие значения может она принимать, если R [1; 2].
836.Объём цилиндра равен 27π. Определите, какую наименьшую площадь боковой поверхности может иметь такой цилиндр.
837.Площадь боковой поверхности цилиндра составляет половину площади его полной поверхности, диагональ осевого сечения – 5. Найдите площадь полной поверхности цилиндра.
838.В цилиндр вписана правильная n - гольная призма. Найдите отношение объёмов призмы и цилиндра, если: а) n = 3; б) n = 4; в) n = 6; г) n = 8; д) n – произвольное целое число.
36
839.В цилиндр вписана призма, основанием которой является прямоугольный треугольник
скатетом a и прилежащим к нему углом α. Найдите объём цилиндра, если высота призмы равна h.
§2. Конус (рассматриваем только прямой круговой конус).
. Конус. Основные понятия.
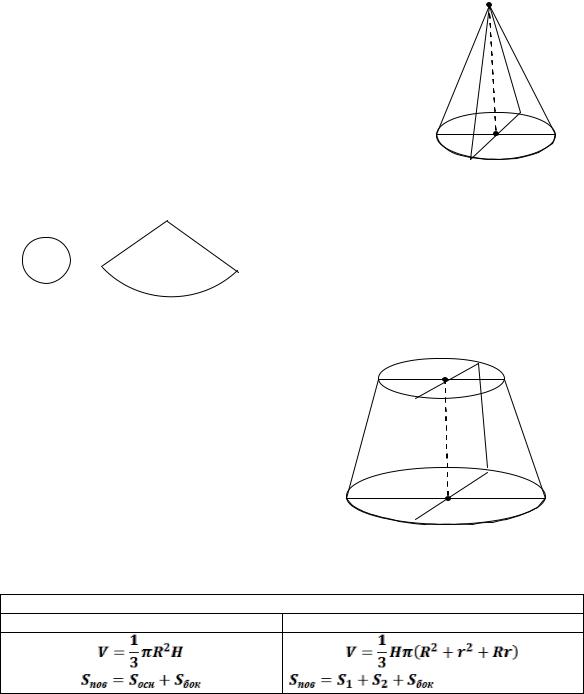
Определение. Конусом называется геометрическая фигура, полученная вращением прямоугольного треугольника вокруг одного из его катетов. Катет, относительно которого происходит вращение – ось конуса, численно равная его высоте; второй катет – радиус основания; гипотенуза – образующая (образует при вращении боковую поверхность конуса).
М – вершина конуса, О – центр основания, МО – ось конуса, МО = Н – высота конуса, ОА = ОВ =…= R – радиус основания,
АМ = BM =…= l – образующая конуса.
Осевое сечение конуса – равнобедренный треугольник (например, треугольник
AMB).
Сечение конуса плоскостью, параллельной основанию – круг, подобный основанию.
M
B
O
A
|
|
l |
l |
Развёртка поверхности конуса состоит из |
||
|
R |
|
|
круга и сектора круга. |
|
|
. Усечённый конус. |
|
|
||||
|
|
|
|
|||
Определение. Усечённым конусом |
|
|
B1 |
|||
называется геометрическая фигура, |
|
|
||||
r |
|
|||||
полученная вращением прямоугольной |
|
|||||
|
|
|
||||
трапеции вокруг её меньшей боковой |
A1 |
|
l |
|||
|
||||||
стороны. Другими словами: усечённым |
|
|||||
|
|
|||||
|
H |
|
||||
конусом называется часть конуса, |
|
|
||||
|
|
|
||||
заключённая между основанием и |
|
|
B |
|||
параллельным основанию сечением конуса. |
|
|
||||
R |
|
|
||||
Осевое сечение – равнобедренная трапеция |
|
|
||||
|
|
|
||||
(например, АВВ1А1). |
|
|
|
|
||
|
|
|
|
A |
|
|
. Объём и площадь поверхности конуса.
|
Конус |
полный |
усечённый |
37

Здесь R – радиус нижнего основания, r – радиус верхнего основания, H – высота, l – образующая.
В конус всегда можно вписать шар. Центр шара лежит на оси конуса и совпадает с
!центром окружности, вписанной в треугольник, являющийся осевым сечением конуса.
Около конуса всегда можно описать шар. Центр шара лежит на оси конуса и
!совпадает с центром окружности, описанной около треугольника, являющегося осевым сечением конуса.
Вопросы и задачи
840.Из бумаги свёрнут кулёк, имеющий форму конуса с радиусом основания 5 см и высотой 10 см. Определите площадь поверхности кулька.
841.Образующая конуса равна 2 см, а радиус основания – 1 см. Объясните, больше или меньше 6 см2 площадь его полной поверхности.
842.Найдите площадь полной поверхности конуса, если:
а) радиус его основания равен 2, а образующая – 4; б) радиус основания равен 3, а высота - 4;
в) радиус основания равен 4, а угол наклона образующей к основанию равен 300.
843. Найдите объём конуса, если:
а) радиус его основания равен 2, а его высота равна 3; б) радиус его основания равен 3, а образующая равна 5;
в) радиус основания равен 2, а образующая наклонена к плоскости основания под углом 30°; г) радиус основания равен 3, а площадь осевого сечения равна 12.
844.Прямоугольный треугольник с катетами a и b (a < b) вращается сначала вокруг одного из них, а затем вокруг другого. Сравните:
а) площади боковых поверхностей полученных конусов; б) площади полных поверхностей получившихся конусов.
845.Равнобедренный прямоугольный треугольник с катетами длины 2 вращают вокруг гипотенузы. Найдите площадь получившейся поверхности.
846.Прямоугольный треугольник с катетами 3 и 4 вращают вокруг гипотенузы. Найдите площадь получившейся поверхности.
38
847.Прямоугольный треугольник с катетами 6 см и 8 см вращается вокруг меньшего катета. Вычислите площади боковой и полной поверхностей образованного при этом вращении конуса.
848.Прямоугольный треугольник с катетами a и b вращают вокруг гипотенузы. Найдите объём полученного тела вращения.
849.Параллелограмм со сторонами 6 см и 8 см и углом 600 вращают вокруг прямой, содержащей большую сторону параллелограмма. Найдите площадь получившейся поверхности.
850.Угол между образующей и осью конуса равен 45°, образующая равна 6,5 см. Найдите площадь боковой поверхности конуса.
851.Площадь осевого сечения конуса равна 0,6 см². Высота конуса равна 1,2 см. Вычислите площадь полной поверхности конуса.
852.Найдите объём конуса, если площадь его основания равна Q, а площадь боковой поверхности равна P.
853.Высота конуса равна диаметру его основания. Найдите объём конуса, если его высота равна H.
854.Найдите объём конуса, если его образующая равна 13 см, а площадь осевого сечения равна 60 см².
855.Радиусы оснований усечённого конуса равны 3 м и 6 м, а образующая равна 5 м. Найдите объём усечённого конуса.
856.Рассматривается конус с радиусом основания 5 см и образующей 3см. Через точку образующей, находящуюся на расстоянии 1 см от вершины, проведено сечение, параллельное основанию конуса. Выполните последовательно такие задания:
а) найдите площадь этого сечения; б) найдите площадь боковой поверхности данного конуса;
в) найдите площадь боковой поверхности конуса, отсекаемого проведённой плоскостью; г) найдите площадь боковой поверхности усечённого конуса, отсекаемого
проведённой плоскостью; д) найдите площадь полной поверхности этого усечённого конуса.
857.Найдите образующую усечённого конуса, если радиусы оснований равны 3 см и 6 см, а высота равна 4 см.
858.Площадь основания конуса равна 12 см², его высота – 6 см. Найдите площадь его сечения, параллельного основанию и проведённого:
а) через середину высоту; б) на расстоянии 2 см от вершины конуса;
в) на расстоянии 4 см от вершины конуса.
Найдите объёмы конусов, у которых основаниями являются рассмотренные сечения, а вершиной – вершина данного конуса.
859.Площадь основания конуса равна 25 см², а высота равна 5 см. На расстоянии 1 см от вершины проведено сечение, параллельное основанию. Найдите объём усечённого конуса, отсекаемого проведённым сечением.
39
860.Высота конуса равна 5 см. На расстоянии 2 см от вершины его пересекает плоскость, параллельная основанию. Найдите объём исходного конуса, если объём меньшего конуса, отсекаемого от исходного, равен 24 см³.
861.В усечённом конусе известны высота h, образующая l и площадь S боковой поверхности. Найдите площадь осевого сечения и объём усечённого конуса.
§ 3. Шар и сфера.
. Шар и сфера. Основные понятия.
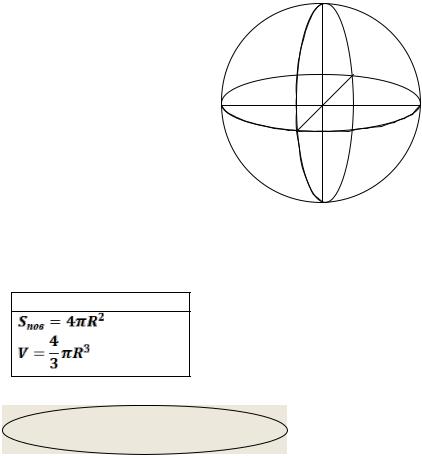
Определение. Шар – геометрическая фигура, полученная вращением круга (полукруга) вокруг его диаметра. Другими словами: шаром называется множество точек пространства, находящихся на расстоянии, не большем данного (R - радиус шара) от данной точки (центра шара).
Определение. Сфера – геометрическая фигура, полученная вращением окружности (полуокружности) вокруг её диаметра. Другими словами: сферой называется множество точек пространства, удалённых от данной точки (центра сферы) на данное расстояние R (радиус сферы).
О – центр шара (сферы). |
|
|
Радиус шара (сферы) – отрезок, |
|
|
соединяющий центр шара с любой |
|
|
точкой на поверхности шара |
|
|
(например, OА). |
A |
O |
|
||
|
|
. Объём и площадь поверхности шара.
Шар
Вопросы и задачи
862. Объясните, как изменится площадь сферы, если её радиус:
а) увеличится в 10 раз; б) уменьшится вдвое.
40
