
23-11-2015_20-04-52 / для студентов гл.7-10
.pdf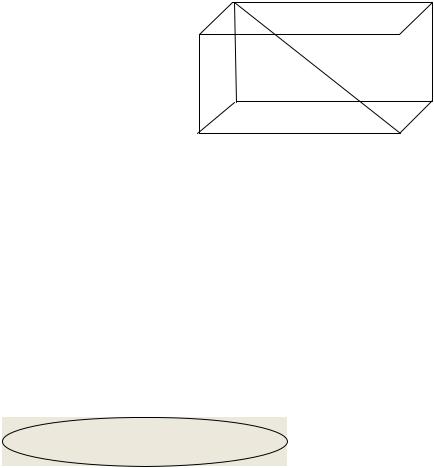
–все боковые грани – прямоугольники;
–все двугранные углы при рёбрах основания прямые;
–высота прямой призмы равна её боковому ребру.
Определение. Правильной призмой называется прямая призма, основания которой – правильные многоугольники.
Частным случаем четырёхугольной призмы является параллелепипед.. Параллелепипед. Куб.
Определение. Параллелепипедом называется призма, основания которой – параллелограммы.
Для параллелепипеда справедливы следующие утверждения:
–все грани параллелепипеда – параллелограммы;
–противоположные грани параллелепипеда равны и параллельны;
–диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам. Определение. Параллелепипед называется прямым, если его боковые рёбра
перпендикулярны основаниям, то есть его боковые грани – прямоугольники.
Определение. Прямой параллелепипед называется прямоугольным, если его основания – прямоугольники.
Все диагонали прямоугольного
параллелепипеда равны; справедливо равенство: d2 = a2 + b2 + c2, где d –
диагональ, a, b, c – три измерения прямоугольного параллелепипеда.
|
d |
|
|
c |
|
a |
|
b |
|
|
Определение. Кубом (гексаэдром) называется прямоугольный параллелепипед с равными рёбрами. Его гранями являются равные квадраты.
. Объём и площадь поверхности призмы, прямоугольного параллелепипеда и куба.
|
Прямоугольный |
|
Призма |
параллелепипед с |
куб с ребром a |
|
измерениями a,b,c |
|
V = Sосн·H |
V = abc |
V = a3 |
Sпов = 2 Sосн + Sбок |
Sпов =2(ab + ac + dc) |
Sпов = 6a2 |
Здесь и далее: V – объём, Sпов – площадь полной поверхности, Sосн – площадь основания, Sбок – площадь боковой поверхности.
Вопросы и задачи
721. Найдите площадь полной поверхности прямоугольного параллелепипеда
ABCDA1B1C1D1, если
а) ABCD – квадрат со стороной 2, а AA1 = 3;
б) AB = 6, AC = 10, AB1 = 10;
21
в) ABCD – квадрат со стороной 4, а диагональ AC1 = 6;
г) ABCD – квадрат со стороной 4, а диагональ AC1 наклонена к основанию под углом 450;
д) AB = 2, BC = 4, а плоскость AB1C1 наклонена к плоскости ABC под углом 600.
722.Найдите объём прямоугольного параллелепипеда, если:
а) его измерения 2 см, 3 см и 4 см; б) площадь его основания 3 см², а высота 5 см;
в) диагональ его основания равна 5 м, одна из сторон основания равна 4 м, а высота равна 2 м; г) высота равна 3 см, диагональ его основания равна 2 см, а угол, образованные ею
содной из сторон основания, равен 30°.
723.Объём прямоугольного параллелепипеда равен 80 см³. Найдите: а) его высоту, если площадь основания равна 40 см²; б) площадь его основания, если его высота равна 8 см.
724.Два измерения прямоугольного параллелепипеда равны 10 см и 2 см. Установите: а) может ли такой параллелепипед иметь объём, больший 100 см³; б) может ли такой параллелепипед иметь объём, меньший 20 см³;
в) можно ли такой параллелепипед, имеющий объём, больший 40 см³, поместить внутрь прямоугольного параллелепипеда с измерениями 11 см, 3 см и 1 см.
г) Параллелепипед рассматриваемого вида, объём которого больше 40 см³, но меньше 60 см³, хотят поместить внутрь куба так, чтобы его грани были параллельны граням куба; какую длину ребра должен иметь куб, чтобы это удалось сделать?
725.Резервуар имеет форму прямоугольного параллелепипеда и сделан из бетона. Его внутренние размеры – 10 м, 12 м и 4 м. Толщина бетонных стенок и дна 0,5 м. Найдите объём резервуара и объём бетона, израсходованного на постройку.
726.Взят лист бумаги размером 20х16 см. Из него двумя способами сложили боковые поверхности прямоугольного параллелепипеда с квадратным основанием. Определите, какой из этих параллелепипедов будет иметь больший объём.
727.Ширина комнаты 4 м, длина 5м, а высота потолка 3м. Общая площадь окон и двери 8 м2. Найдите площадь обоев, которыми оклеены стены.
728.Прямоугольный параллелепипед с измерениями 1 м, 3 м и 5 м помещён внутрь куба
сребром 6 м. Сделайте рисунок для такого случая и найдите объём свободного места внутри куба.
729.Диагональ прямоугольного параллелепипеда равна 18 см и составляет угол 30° с плоскостью боковой грани и угол 45° с боковым ребром. Найдите объём параллелепипеда.
730.Диагональ прямоугольного параллелепипеда составляет угол α с плоскостью боковой грани и β с плоскостью основания. Найдите объём параллелепипеда, если его высота равна h.
731.Стороны основания прямоугольного параллелепипеда равны a и b. Диагональ параллелепипеда составляет с боковой гранью, содержащей сторону основания, равную b, угол 30°. Найдите объём параллелепипеда.
22
732.Найдите объём прямоугольного параллелепипеда ABCDA1B1C1D1, если: а) АC1 = 1 м, угол C1АC равен 45°, угол C1АВ равен 60°; б) АC1 = 24 см, угол C1АA1 равен 45°, диагональ АC1 составляет угол 30° с плоскостью боковой грани.
733.Найдите объём прямоугольного параллелепипеда, если:
а) его диагональ равна 1 см, угол, образованные ею с плоскостью основания, равен 45°, а угол, образованный диагональю основания с одной из его сторон, равен 30°;
б) плоскость, проходящая через параллельные и не лежащие в одной боковой грани рёбра верхнего и нижнего оснований, наклонена к основанию под углом 60°, а стороны основания равны 3 см и 4 см.
734.Найдите объём куба, если его диагональ равна d.
735.Измерения прямоугольного параллелепипеда равны 6, 16 и 18. Найдите ребро равновеликого ему куба.
736.В основании прямого параллелепипеда лежит ромб со стороной 2 и острым углом 30°. Высота параллелепипеда равна 3. Найдите объём параллелепипеда.
737.В основании прямого параллелепипеда лежит ромб, диагонали которого равны 4 и 6. Высота параллелепипеда равна 4. Найдите его объём.
738.В основании прямого параллелепипеда лежит параллелограмм. Найдите его объём, если:
а) высота параллелепипеда 3 см, стороны основания 4 см и 5 см, а один из углов основания 135°; б) высота параллелепипеда 5 см, диагонали основания 6 см и 10 см, а угол между диагоналями 30°.
739.Найдите объём прямого параллелепипеда, основание которого параллелограмм, если стороны параллелограмма равны 8 см и 15 см и образуют угол 60°, а меньшая диагональ параллелепипеда составляет с плоскостью основания угол 30°.
740.Рассматривается правильная четырёхугольная призма. Найдите её объём, если: а) её высота равна 2, а диагональ основания 3;
б) диагональ основания равна 3, а диагональ призмы
741.Пусть ABCDA1B1C1D1 – правильная четырёхугольная призма, высота которой равна 2. Объясните:
а) может ли площадь её полной поверхности быть равной 10?
б) какие значения может принимать площадь её полной поверхности, если длина стороны основания принимает все значения из отрезка [ 1; 3].
742.Найдите объём правильной n-угольной призмы, у которой каждое ребро равно a,
если: а) n = 3; б) n = 4; в) n = 6; г) n = 8.
743.В правильной треугольной призме через сторону нижнего основания и противолежащую ей вершину верхнего основания проведено сечение, составляющее угол 60° с плоскостью основания. Найдите объём призмы, если сторона основания равна a.
744.Наибольшая диагональ правильной шестиугольной призмы равна 8 см и составляет
сбоковым ребром угол 30°. Найдите объём призмы.
23
745.Основание прямой призмы – треугольник со сторонами 5 см и 3 см и углом 120° между ними. Наибольшая из площадей боковых граней равна 35 см². Найдите площадь боковой поверхности призмы.
746.В основании прямой призмы лежит треугольник. Найдите её объём, если:
а) её высота равна 3, а стороны основания 3, 4 и 5; б) её высота равна 2, а все стороны основания равны 3;
в) её высота равна 1, а стороны основания равны 13, 13 и 10; г) её высота равна 5, две стороны основания равны 3 и 4, а угол между ними равен
45°.
747.В основании прямой призмы с высотой, равной 5, лежит трапеция. Найдите объём призмы, если:
а) трапеция прямоугольная с основаниями 4 и 2 и высотой 3; б) трапеция равнобедренная с боковыми сторонами длины 10 и основаниями 18 и
6.
748.Найдите объём прямой призмы АВСА1В1С1, если АВ=ВС=m, угол ABC равен φ и ВВ1 = BD, где BD – высота треугольника АВС.
749.Основанием прямой призмы является параллелограмм. Через сторону основания, равную a, и противолежащую ей сторону другого основания проведено сечение, составляющее угол β с плоскостью основания. Площадь сечения равна Q. Найдите объём данной призмы.
750.Найдите объём треугольной призмы АВСА1В1С1, высота которой 3, если:
а) АВС – прямоугольный треугольник с катетами 2 и 4; б) АВС – равносторонний треугольник со стороной 1.
751.Найдите объём треугольной призмы АВСА1В1С1, если:
а) площадь основания АВС равна 5 см², а боковое ребро АА1 равно 2 см и наклонено к плоскости основания под углом 30°;
б) АВС – равносторонний треугольник со стороной 3 см, а боковое ребро ВВ1 равно 3 см и наклонено к плоскости основания под углом 45°.
в) АВС – треугольник со сторонами 5, 12 и 13, а высота А1М грани АА1В1В наклонена к плоскости основания под углом 60° и равна 2.
г) АВС – треугольник со сторонами 6, 8 и 10, высота боковой грани АА1В1В равна 4,
а угол между основанием и этой гранью равен 45°.
752.Рассматривается единичный куб ABCDA1B1C1D1. В куб хотят поместить призму, объём которой равен 0,5, так, чтобы её основанием был треугольник АВС. Объясните, удастся ли это сделать.
753.Найдите объём параллелепипеда ABCDA1B1C1D1, если:
а) его основанием служит квадрат со стороной 1, а боковое ребро наклонено к плоскости основания под углом 30° и равно 2; б) его основание – параллелограмм со сторонами 2 и 3 и острым углом 45°, а
боковое ребро наклонено к плоскости основания под углом 60° и равно 2;
в) его основание ABCD – прямоугольник со сторонами АВ = 6 см и AD = 8 см, вершина A1 проектируется в точку пересечения диагоналей прямоугольника, а грань АА1В1В наклонена под углом 30° к основанию.
24
754.Грани ABCD и АА1В1В параллелепипеда ABCDA1B1C1D1 – квадраты. Ребро АA1 наклонено под углом 45° к плоскости АВС, АВ = 2.
а) Найдите объём данного параллелепипеда.
б) Найдите высоту параллелепипеда, опущенную из точки С на грань АА1В1В.
755.Основанием наклонного параллелепипеда является прямоугольник со сторонами a
иb. Боковое ребро равно и составляет со смежными сторонами основания углы, равные φ. Найдите объём параллелепипеда.
756.Все грани параллелепипеда – равные ромбы, диагонали которых равны 6 см и 8 см. Найдите объём параллелепипеда.
§2. Пирамида.
. Пирамида. Правильная пирамида.
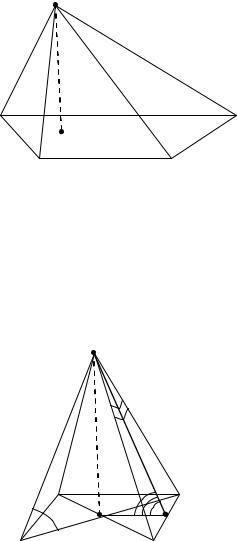
Определение. Пирамидой называется многогранник, одна грань которого - произвольный многоугольник (основание), а все остальные грани (боковые) – треугольники, имеющие общую вершину (вершина пирамиды).
Определение. Высотой пирамиды называется перпендикуляр, проведённый из вершины пирамиды на плоскость её основания.
M – вершина пирамиды
MO – высота пирамиды
MO ABC
MO∩ ABC = O
M
A B O
D C
четырехугольная пирамида
Определение. Пирамида называется правильной, если её основание – правильный многоугольник и высота пирамиды проходит через центр этого многоугольника.
Определение. Высота боковой грани правильной пирамиды, проведённая из её
вершины, называется апофемой. |
|
|
|
|
|
Правильная четырёхугольная пирамида |
|
|
|
|
|
MABCD: Основание ABCD – квадрат, |
|
|
|
M |
|
изображаемый параллелограммом. |
|
|
|
|
|
МО – высота пирамиды, проходит через |
|
|
|
|
|
центр О квадрата ABCD – точку |
|
|
|
|
|
пересечения его диагоналей. |
|
|
|
|
|
МК – апофема |
|
|
|
|
|
МКО – линейный угол двугранного угла |
|
|
|
|
|
с ребром CD (угол между боковой гранью |
|
B |
|
|
C |
DMC и основанием ABCD) |
|
|
|
||
|
|
|
|
|
|
МАО – угол между боковым ребром МА и |
|
|
|
|
K |
плоскостью основания |
|
|
О |
|
|
A |
|
|
D |
||
DMC – плоский угол при вершине |
|
|
|
||
|
|
|
|||
|
|
|
|
|
|
пирамиды |
|
|
|
|
|
25 |
|
|
|
|
|

Правильная треугольная пирамида MABС: |
|
M |
|
|
|
|
|
АВС – правильный (равносторонний), |
|
|
|
высота МО пирамиды проходит через точку |
|
|
|
О – пересечение медиан (высот, |
|
|
|
биссектрис) АВС. |
|
|
|
Если все грани правильной пирамиды – |
|
|
|
равносторонние треугольники, то такая |
|
|
B |
пирамида называется правильным |
C1 |
|
|
тетраэдром. |
|
A1 |
|
|
|
||
A |
|
О |
C |
B1 |
|
||
|
|
|
Для решения задач полезно знать.
Для правильной пирамиды справедливы следующие утверждения:
–боковые рёбра равны между собой;
–боковые рёбра одинаково наклонены к плоскости основания;
–боковые грани – равные друг другу равнобедренные треугольники;
–боковые грани одинаково наклонены к плоскости основания (т.е. все двугранные углы при рёбрах основания равны);
–апофемы равны;
–плоские углы при вершине равны.
Для пирамиды, все боковые рёбра которой равны между собой, справедливы следующие утверждения:
–все боковые рёбра одинаково наклонены к плоскости основания;
–около основания можно описать окружность, вершина пирамиды проецируется в центр этой окружности;
–около такой пирамиды можно описать шар, центр которого лежит на прямой, содержащей высоту пирамиды.
Для пирамиды, все двугранные углы при рёбрах основания которой равны между собой, справедливы следующие утверждения:
–в основание можно вписать окружность, вершина пирамиды проецируется в центр этой окружности;
–в такую пирамиду можно вписать шар, центр которого лежит на высоте пирамиды.
. Усечённая пирамида.
Определение. Усечённой пирамидой называется многогранник, две грани которого – подобные многоугольники, лежащие в параллельных плоскостях, называемых основаниями пирамиды, а
B1
A1 |
C1 |
|
B
26
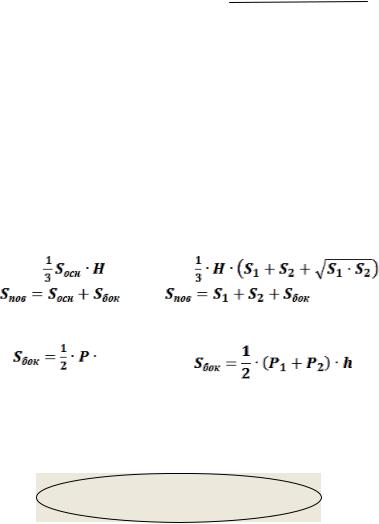
остальные грани – четырёхугольники |
|
|
(трапеции), называемые боковыми |
|
|
гранями. Другими словами: |
A |
|
усечённой пирамидой называется |
C |
|
часть полной пирамиды, заключённая |
усеченная треугольная пирамида АВСА1В1С1 |
|
между основанием и параллельным |
|
|
ему сечением.
Определение. Усечённая пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию. Боковые грани правильной усечённой пирамиды – равнобедренные трапеции, а её основания – правильные, подобные друг другу многоугольники.
. Объём и площадь поверхности пирамиды.
|
Пирамида |
|
полная |
|
усечённая |
V = |
|
V = |
Для правильной |
|
Для правильной усечённой |
пирамиды: |
|
пирамиды: |
h |
|
|
|
|
|
Здесь S1 и S2 – площади нижнего и верхнего оснований, P – периметр основания, P1 и P2 – периметры нижнего и верхнего оснований, h – апофема.
Вопросы и задачи
757.Найдите объём пирамиды с высотой H, если:
а) H = 2 м, а основанием служит квадрат со стороной 3 м;
б) H= 2,2 м, а основанием служит треугольник АВС, в котором АВ = 20 см, ВС = 13,5 см, угол АВС равен 30°.
758.Найдите объём правильной треугольной пирамиды, высота которой равна 12 см, а сторона основания равна 13 см.
759.Для молока из картона склеен пакет, имеющий форму правильного тетраэдра с ребром 10 см. Найдите площадь потраченного картона.
760.Молоко планируют разливать в пакеты, имеющие форму прямоугольного параллелепипеда с высотой 20 см и квадратным основанием, сторона которого 7 см, и в пакеты, имеющие форму правильного тетраэдра с ребром 15 см. Укажите, в какие пакеты входит больше молока.
761.Найдите объём правильной четырёхугольной пирамиды, все рёбра которой 2.
762.Рассматривается четырёхугольная пирамида MABCD такая, что в основании её лежит квадрат со стороной 2, а её высота MA равна 3. Найдите площадь поверхности этой пирамиды.
27
763.Вычислите площадь боковой поверхности правильной треугольной пирамиды, если её высота равна 9, апофема – 18.
764.В правильной шестиугольной пирамиде апофема равна 15, высота – 12. Найдите площадь полной поверхности пирамиды.
765.Пусть KMNLP и ABCDA1B1C1D1 соответственно правильная четырёхугольная пирамида и правильная призма, имеющие равные высоты длины 1 и равные стороны оснований длины 2. Сравните их объёмы и площади полных поверхностей.
766.Пирамида равновелика кубу с ребром 1 и основанием её является грань куба. Найдите её высоту.
767.Рассматривается куб ABCDA1B1C1D1 с ребром 1. Назовите какую-либо пирамиду с
вершинами в вершинах куба, такую, что её объём равен: а)  ; б)
; б)  .
.
768.Площадь основания пирамиды SABC равна 4 см², а высота – 2 см. Через середину высоты проведено сечение MNK, параллельное основанию. Найдите:
а) объём пирамиды SABC; б) объём пирамиды SMNK;
в) объём тела ABCMNK, ограниченного основанием пирамиды и плоскостью MNK (усечённой пирамиды).
769.Рассматривается правильная треугольная пирамида MABC, сторона основания которой равна 4, а угол наклона плоскости боковой грани MAB к плоскости основания равен 60°. Пусть MO – высота пирамиды, точка K – середина ребра AB. Найдите:
а) длину отрезка OK; б) длину высоты MO;
в) площадь основания ABC; г) объём пирамиды MABC.
770.Найдите объём треугольной пирамиды MABC, если:
а) все плоские углы с вершиной А прямые и AM = AB = AC = 1 см;
б) АВС – правильный треугольник со стороной 2 см, а ребро МА равно 3 см и наклонено к плоскости основания под углом 30°; в) АВС – равнобедренный треугольник со сторонами АВ = ВС = 2 см и углом АВС =
120°, грань МАВ имеет площадь, равную 4 см², и перпендикулярна основанию АВС; г) АВС – прямоугольный треугольник, гипотенуза АВ которого равна 13 см, а катет АС = 12 см, вершина М проектируется в середину гипотенузы АВ, грань МАС образует с основанием угол 45°; д) она является правильной пирамидой, ребро основания которой равно 2 см, а
боковое ребро наклонено к плоскости основания под углом 45°; е) она является правильным тетраэдром, все рёбра которого равны 1.
771.Все рёбра правильной четырёхугольной пирамиды SABCD равны а. Найдите: а) плоский угол при вершине S; 600
б) угол ACS;
в) высоту пирамиды; г) угол наклона бокового ребра к основанию;
д) угол наклона боковых граней к основанию.
772.Высота правильной треугольной пирамиды SABC равна 3 а высота её основания равна 9. Найдите:
а высота её основания равна 9. Найдите:
28
а) боковое ребро; б) апофему;
в) сторону основания;
г) плоский угол при вершине S;
д) угол наклона боковой грани к основанию.
773.Высота правильной четырехугольной пирамиды SABCD равна h, а сторона основания равна а. Найдите:
а) диагональ основания; б) боковое ребро; в) апофему;
г) расстояние от точки пересечения диагоналей основания O до плоскости боковой грани;
д) расстояние от вершины A до плоскости SCD.
774.Сторона основания правильной шестиугольной пирамиды равна 2 , высота
, высота
пирамиды равна 4. Найдите: а) боковое ребро;
б) высоту основания пирамиды; в) апофему;
г) расстояние от центра основания O до плоскости боковой грани; д) расстояние от вершины A до плоскости BSC.
775. Все боковые рёбра пирамиды равны 10, а радиус окружности, описанной около её основания, равен 8. Найдите высоту пирамиды.
776.Найдите объём четырёхугольной пирамиды MABCD, если ABCD – квадрат со стороной 4 и вершина М проецируется:
а) в точку А, а МВ = 5; б) в точку В и ребро МА наклонено к плоскости основания под углом 45°;
в) в точку С и грань MAB наклонена к плоскости основания под углом 30°.
777.Найдите площадь боковой поверхности правильной треугольной пирамиды MABC, если:
а) MA = 5, AB = 6;
б) AB = 2, а высота пирамиды MO = 1;
в) AB = 2 и медиана боковой грани (апофемы) MK наклонена к плоскости основания под углом 300;
г) высота MO равна 3, а плоскость боковой грани MAB наклонена к плоскости основания ABC под углом 450.
778.Основанием пирамиды является параллелограмм, стороны которого равны 20 см и 36 см, а площадь равна 360 см². Высота пирамиды проходит через точку пересечения диагоналей основания и равна 12 см. Найдите площадь боковой поверхности пирамиды.
779.Основанием пирамиды является параллелограмм со сторонами 5 м и 4 м и меньшей диагональю 3 м. Высота пирамиды проходит через точку пересечения диагоналей основания и равна 2 м. Найдите площадь полной поверхности пирамиды.
29
780.Основанием пирамиды является квадрат, одно из боковых рёбер перпендикулярно к плоскости основания. Плоскость боковой грани, не проходящей через высоту пирамиды, наклонена к плоскости основания под углом 45°. Наибольшее боковое ребро равно 12 см. Найдите: а) высоту пирамиды; б) площадь боковой поверхности пирамиды.
781.Основанием пирамиды DABC является треугольник АВС, у которого АВ = АС = 13 см, ВС = 10 см; ребро AD перпендикулярно к плоскости основания и равно 9 см. Найдите площадь боковой поверхности пирамиды.
782.Основанием пирамиды DABC является прямоугольный треугольник АВС, у которого гипотенуза АВ равна 29 см, катет АС равен 21 см. Ребро DA перпендикулярно к плоскости основания и равно 20 см. Найдите площадь боковой поверхности пирамиды.
783.Основанием пирамиды является прямоугольник, диагональ которого равна 8 см. Плоскости двух боковых граней перпендикулярны к плоскости основания, а две другие боковые грани образуют с основанием углы 30° и 45°. Найдите площадь поверхности пирамиды.
784.Основание пирамиды – квадрат со стороной 16 см, две боковые грани перпендикулярны плоскости основания. Вычислите площадь полной поверхности пирамиды, если её высота равна 12 см.
785.Основанием пирамиды является треугольник со сторонами 12 см, 10 см и 10 см. Каждая боковая грань наклонена к основанию под углом 45°. Найдите площадь боковой поверхности пирамиды.
786.Основание пирамиды – прямоугольный треугольник, катеты которого равны 3 и 4. Каждая боковая грань наклонена к плоскости основания под углом 60°. Найдите площадь полной поверхности пирамиды.
787.Основание пирамиды – ромб с диагоналями, равными 6 м и 8 м. Высота равна 1 м. Вычислите площадь полной поверхности пирамиды, если все двугранные углы при основании равны.
788.Основанием пирамиды является ромб со стороной 6 см. Каждый из двугранных углов при основании равен 45°. Найдите объём пирамиды, если её высота равна 1,5 см.
789.Основание пирамиды – ромб со стороной 15 см, каждая грань пирамиды наклонена к основанию под углом 45°. Найдите объём пирамиды, если площадь её боковой поверхности равна 300 см².
790.Основание пирамиды – равнобедренная трапеция, у которой параллельные стороны составляют 3 см и 5 см, а боковая сторона – 7 см. Высота пирамиды проходит через точку пересечения диагоналей основания, а большее боковое ребро равно 10 см.
Найдите объём пирамиды.
791.Основание пирамиды – прямоугольник, площадь которого равна 1 м². Две боковые грани перпендикулярны основанию, а две другие наклонены к нему под углами 30° и 60°. Найдите объём пирамиды.
792.Основание пирамиды – прямоугольный треугольник с катетом a и прилежащим к нему углом 30°. Боковые рёбра наклонены к плоскости основания под углом 60°. Найдите объём пирамиды.
793.Основание четырёхугольной пирамиды – прямоугольник с диагональю b и углом α между диагоналями. Боковые рёбра наклонены к плоскости основания под одним и тем же углом. Найдите этот угол, если объём пирамиды равен V.
30
