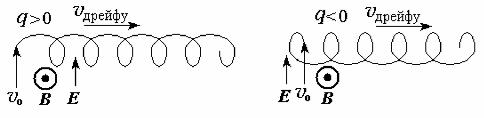MexLekcii2010prn
.pdf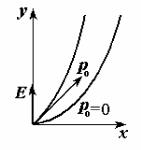
11
=0,
dp |
= qE . |
(3) |
|
||
dt |
|
|
(3), D ,
=const,
0;
( v).
,
Y, Y.
( t = 0):
ìE = {0, Ey ,0} = Ey |
|
|
ï |
,0} |
(4) |
íp0 = {p0x , p0y |
||
ï |
= 0 |
|
îr(0) = {0,0,0} |
|
|
(3) :
|
dp |
x |
= 0 ; |
|
dpy |
= qE |
|
|
dp |
x |
= 0; |
dp |
y |
= qE |
y |
dt |
(5) |
|
|
|
|
|
|||||||||||||
|
dt |
|
dt |
y |
|
|
|
|
|
|
|
|
|||||
(4) |
|
||||||||||||||||
px |
py |
t |
|
|
(t) = 0 , |
(t) = qEyt + p0y |
|
||||||||||
òdpx = 0, |
òdpy = òqEydt = qEyt |
(6) |
|||||||||||||||
p0 x |
p0 y |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
( m=m0=const, p(t)=mv(t) ):
vx (t) = v0x ; vy (t) = |
qEy |
t + v0y |
m |
dx(t) |
= p0x |
; m |
dy(t) |
= qEy t + p0y |
. (6 ) |
|
m |
dt |
dt |
||||||||
|
|
|
|
|
|
|
(6 ) r(t): r(0)=0 ( (0)=0, (0)=0)
|
p |
0x |
|
t qEy |
t p0y |
|
qEy t 2 |
p0y |
|
|||||
x(t) = |
|
t ; ( ) |
y(t) = ò |
|
tdt + ò |
|
dt = |
|
|
|
+ |
|
t . ( ) (7) |
|
|
|
m |
m |
|
|
m |
||||||||
|
m |
0 |
0 |
|
m 2 |
|
||||||||
( ) t ( ) (
7), :
t = |
m × x(t) |
(7, ) y = |
qEy |
|
m2x2 |
+ |
p0y m |
× x |
= |
qEym |
x |
2 |
+ |
p0y |
x . (8) |
||
|
|
|
|
|
|
|
|
|
|
|
|||||||
p |
2m p2 |
m p |
0x |
2p2 |
|
p |
|||||||||||
|
|
|
|
|
|
|
|
||||||||||
|
0x |
|
|
|
0x |
|
|
|
|
|
0x |
|
|
|
0x |
|
|
– ( . .1).
, 0=0 (
) (6) (6 ) :
p |
y |
(t) = qE t ; (9) |
v |
y |
(t) = |
qEy |
t , |
(9 ) |
|
|
|
||||||||
|
y |
|
|
m |
|
|
|||
. |
|
||||||||
v > , , |
. 1 |
||||||||
81
11
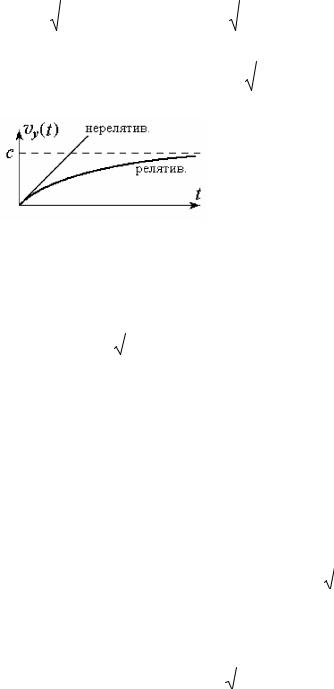
v (t)<<c, , t << mc (qEy ) ( (9),
(qEy ) ( (9),
v ).
(9) :
|
m0vy |
|
|
|
|
vy |
|
qEyt |
c2 - vy2 |
æ m c ö2 |
|
c2 |
|
||||||
|
|
|
|
= qE t |
|
|
|
|
= |
|
|
|
= ç |
0 |
|
÷ |
= |
|
-1. |
|
|
|
|
|
|
|
|
|
v2 |
|
|
v2 |
|||||||
2 |
/ c |
2 |
y |
c |
2 |
2 |
|
m c |
ç qE |
t ÷ |
|
|
|||||||
1 - vy |
|
|
|
|
- vy |
|
0 |
|
y |
è |
y |
ø |
|
y |
|
||||
: |
vy |
(t) = |
|
c |
|
|
. ( >1, v < c, .2.) |
|
|
|
|
|
|||||
1 + (m c / qE t)2 |
||||||||
|
|
|
|
|||||
|
|
|
0 |
y |
|
|||
F=qEy,
U
: DU=–qEyy.
. 2 .
= 2, – .
v<0,5 ) :
mc 2 = |
|
m |
c 2 |
|
= m |
c 2 |
|
1 v2 |
) » m |
c 2 |
|
mv2 |
= m |
c 2 + E , |
|
|||
0 |
|
|
(1 + |
|
|
|
+ |
|
(10) |
|||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
1 - v2 / c 2 |
0 |
|
|
2 c 2 |
0 |
|
|
2 |
0 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
0 2 – . , 2 |
|
|||||||||||||||||
, .
|
|
: |
|
= mc2 + U. |
(11) |
, (t=0)
( U=U0 0, ),
mc2 + DU = m0c2 |
|
m c |
2 |
|
- qEy y = m0c 2 . |
|
0 |
|
|
(12) |
|||
|
|
|
||||
|
|
|
||||
|
1- v2 / c2 |
|
||||
,
v ( 10) :
|
1 |
æ |
|
m c2 |
|
2 |
ö |
|
E (v) |
|
|
y = |
|
ç |
0 |
- m0c |
|
÷ |
= |
|
. |
(13) |
|
|
|
|
|
|
|||||||
|
ç |
1 - v2 / c2 |
|
÷ |
qEy |
||||||
|
qEy è |
|
|
ø |
|
|
|
||||
– ,
(10) ( 13).
, , ,
, , (
. 3), (12) (13) :
82
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
+ |
U = 0 |
qE y = |
mv2 |
y = |
1 |
mv2 |
(13 ) |
|||
|
|
|
|
. |
||||||||
|
|
|
|
|
|
y |
2 |
|
qEy |
2 |
|
|
|
|
|
|
|
|
|
|
|
||||
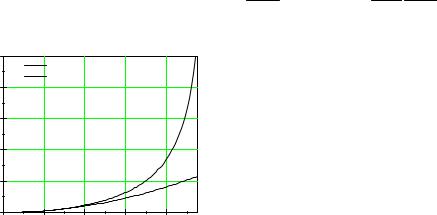
|
1000 |
|
|
|
|
|
(13) |
|
||||
|
1 - |
|
||||||||||
), |
|
|||||||||||
800 |
2 - |
|
( |
|||||||||
|
|
|
|
|||||||||
=1 |
|
|
|
|
1 |
). , |
||||||
|
0,0 |
0,2 |
0,4 |
0,6 |
||||||||
0,8 |
, |
|||||||||||
|
600 |
|
|
|
|
=1 |
|
v=0,9 |
||||
|
400 |
|
|
|
|
700 . |
||||||
|
200 |
|
|
|
2 |
|
|
|
|
|||
|
|
|
|
|
, |
|||||||
|
|
|
|
|
|
|||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
, v/c |
( – |
|||||||||
|
|
. 3 |
|
|
). , |
|||||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|||||||
, |
, |
|||||||||||
), , ,
mv2/2 = |
qEyy ( |
“ ” , |
||||
). , v i y, |
q |
|||||
|
m: |
|
v2 |
|
||
|
|
q |
|
|
||
|
|
|
= |
|
. |
(14) |
|
|
|
|
|||
m2yEy
q/m ( q i m)
( – ):
|
mg = qE |
q/m = g/E. |
(14 ) |
||
|
§4. |
|
|||
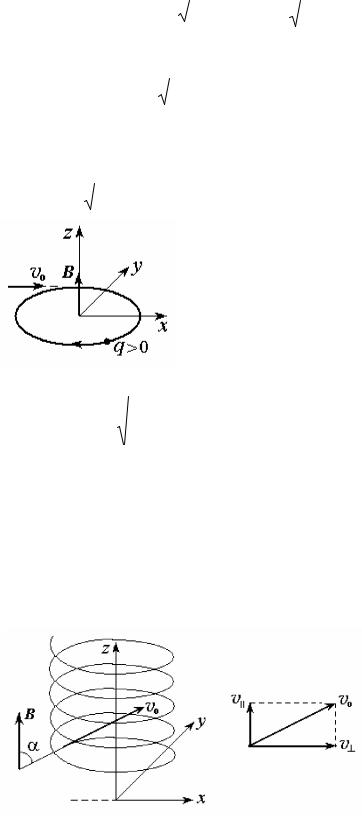
|
=0, =(0,0, z)= z= const, |
v(0)=v0=(v0 ,v0 ,0). |
|||
(1) |
|
|
|||
|
|
dp |
= F = q(v × B) . |
(15) |
|
|
|
|
|||
|
|
dt |
|
|
|
|
|
|
|
|
|
F B , ( Y), dt
dp ,
v0 ( ( Y) ),
( Y). , F v0 ,
( ) , , ,
. t
| v(t) |=| v(0) |= v0 → v2 (t) = v02 = v02x + v02y = const . |
(16) |
83
11
(15) ,
(16), , |
v2 = v02 |
= const: |
|
|
||||||||||
|
d æ |
|
m v |
|
ö |
|
|
|
m |
|
|
dv |
|
|
|
|
ç |
0 |
|
÷ |
= |
|
|
0 |
|
|
|
= q(v ´ B) . |
|
|
|
|
|
|
|
|
|
|
|
|||||
ç |
1 - v2 / c2 |
÷ |
|
|
- v2 |
/ c2 |
dt |
|||||||
|
dt è |
ø |
1 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
, ,
, |
B v , |
|v|=v0 : |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
a = |
dv |
= a |
n |
= |
|
|
|
|
1 - v02 / c2 |
|
|
qv B = |
v02 |
. |
|
|
( |
F |
= F |
|
|
|
® qv B = m |
v02 |
) |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
m0 |
0 |
|
R |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
0 |
|
|
R |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
R = |
v0 |
|
|
|
|
|
|
m0 |
|
|
|
|
|
= |
p0 |
= const |
|
v/c<<1 |
|
|
R = |
mv0 |
= |
p0 |
|
. |
|
(17) |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
qB |
qB |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
qB 1 - v2 |
/ c2 |
|
|
|
|
qB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v0 , |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, v0 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
, |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R , |
||||||||||||||||||||||||||||||||||
|
. 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( . 4); |
|
R |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
( ) . |
||||||||||||||||||||||||||||||||||||||||||
|
|
v |
qB |
|
|
|
v2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
1 |
|
|
|
|
v0<<c |
w = |
|
qB |
, T |
= |
2pR |
= |
2p |
= 2p |
m |
, |
(18) |
|
|||||||||||||||||||||||||||||||||||
w = |
|
0 |
= |
|
|
|
|
- |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
m |
|
c2 |
|
|
|
|
m |
v |
|
|
|
w |
qB |
|
|||||||||||||||||||||||||||||||||||||||
|
|
R |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
w – (w=2 v), – .
(17) (18) ,
, ( ) .
v0 a 90 ,
v0 – v||
v , :
F = q(v ´ B) = q[(v|| + v ) ´ B] = q(v ´ B) + q(v|| ´ B) = q(v ´ B) +0.
, F
( . §1),
( v , ,
v
v : v2 = vx2 + vy2 ),
. 5
84
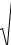
11
, ( . 5).
(a 90 ) (17) (18) :
R = |
mv |
= |
mv0 sin a |
|
, |
T = |
2pR |
= 2p |
m |
|
. |
|
qB |
qB |
v sin a |
qB |
|||||||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
0 |
|
|
|
|
||
(17) (18) q/m
. ,
( ), .
m |
= |
qB |
R . |
(19) |
|
||||
|
|
v |
|
|
, , (q= =1,6×10-19 ).
R,
( , )
,
, .
, ,
,
,
.
, .
mv2 |
|
2qU |
|
|
||
|
= qEL = qU Þ v = |
|
, |
|||
2 |
m |
|||||
|
|
|
|
|||
L i U – , ( ) ( ),
.
(19) :
|
q2R2 |
|
|
m = |
|
B2 . |
(19 ) |
|
|||
a |
2qU |
|
|
|
|
||
, w
,
1932
( ).
,
d=279 (R»14 ,
).
(
) ,
w ( ) . ,
,
w ,
( ) .
85

11
, (
) ~10 (w ~6×107 -1), R=0,5
, v =w ×R = 6×107×0,5 = 3×107 ( ),
= mpv2/2 = 0,5×1,67×10-27×9×1014 » 7,5×10-13 ( ) » 4,7×106 .
B = mpv = 1,67 ×10−27 ×3×107 » 6 ×10−1 ( !). |
|
qR |
1,6 ×10−19 ×0,5 |
§5. .
( , )
, “ ”
, “ ”
(“ ”).
.
,
:
m(Dv)2/2= q(L2–L1)=EqDL , L1=0, v1=0, mv2/2=EqL.
=qDL=qL (pe=q, L=1) (“ ”)
, ( v2/2)/ –
.
,
|
|
mv2 |
|
mv2 |
|
|
p = |
|
= |
|
= const , – |
|
|
||||
|
|
2B |
|
2B |
|
|
|
|
|||
v ( v|| ,
v v ).
(mv2/2=const), , v2 = v2 + v||2 = const v
v||. ,
, ,
( ) v|| 0
.
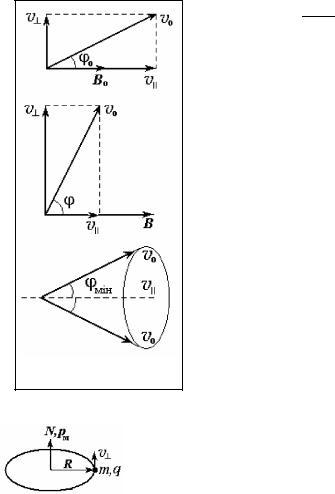
“ ” ( ).
v
. 6. j0 – “ ”
.
( , v = v0 sin j ) : |
|
|
sin 2 j |
|
|
|||||
|
|
v2 |
v2 |
sin 2 j |
|
|
||||
p 0 = |
|
0 |
= |
|
Þ |
0 |
= |
|
. |
(20) |
|
|
|
B |
|||||||
|
|
B0 |
B |
B0 |
|
|
||||
86
11
, j = 90 , v = v0, v|| = 0,
|
|
– |
|
||||||
|
|
“ ” . |
|
sin j =1, |
|||||
|
|
, (20), |
|||||||
|
|
B = |
B0 |
B = |
|
B0 |
|
||
|
|
|
; |
|
|
. |
|||
|
|
sin2 j |
sin |
2 j |
|||||
|
|
0 |
|
|
|
|
|
||
|
|
, |
|||||||
|
|
|
|||||||
|
|
, |
, |
“ |
|||||
|
|
” j>j . “ ” |
|||||||
|
|
) , |
v0 |
||||||
|
|
( ) ( . . 6, |
|||||||
|
|
, |
|||||||
|
|
, ). |
|||||||
|
|
|
|||||||
|
. 6 |
|
|||||||
, , |
|
||||||||
, .
.
|
|
mv2 |
ì |
mv |
|
ü |
|
mv |
|
|
v |
|
|
1 |
|
|
|
1 |
|
|
|
p |
= |
|
= íR = |
|
ý |
= |
|
|
|
q = |
|
Rv |
q Þ p |
= |
|
(R ´ v |
|
)q |
|||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
m |
2B |
î |
qB þ |
|
qB |
2 |
|
2 |
|
|
|
2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
– N = (R×v)m, – q.
,
.
, .
, , (
, q>0), v.
:
,
, ,
(R=mv/qB, . 7).
Fe
( ).
. 1
, , . , ,
, ,
7. .
87