Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Ужгородский национальный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

MexLekcii2010prn

.pdf

Скачиваний:

Добавлен:

02.03.2016

Размер:

1.71 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 207 8 9 10 11 12 13 14 15 16 17 18 19 20 > Следующая >>>

. . .


,
	.	,
	. ,

m=dM/dt.

( )

, .

, t

(t), v.

dt , 0 . ,

( , .),

, F. 0 ,

“ - 0”, – –

. ,

. t,

0, ( ) 0 = v. (t + dt)

( - 0), (v+dv), 0,

. dt

, :

dP = P–P0 = Fdt Þ (M–m0)×(v+dv) + m0u – Mv = Fdt

(1)

Mv + Mdv – m0v –×m0dv + m0u – Mv = {m0dv – }

= Mdv m0v + m0u = Mdv + ( – v )m0 = Fdt .

(2)

V – ,

0 . ,

0, ,

(1). ,

dM=M(t+dt)–M(t), (

0 , dM>0), (

, dM<0), , , 0 dM,

, : m0 = –dM.

(1): dM<0, m0>0 ( ), ( –0), , ( + 0),

( – 0), dM>0 m0 = –dM<0 , –(– 0)= + 0.

, (2), 0 –dM, ( –v) V:

Mdv – VdM = Fdt

- V

= F .

(2 )

= F + V

Ma = F + Fp.

(3)

– ,

1897 , – ( ), , v –

, V – ( )

( ) , Fp – . ,

V dM = Fp ,

, .

m – ( ) (

), ( dM/dt<0)

(3)

M	dv	= F - mV .	(4)

	dt

Fp=-mV ( ) V

. ,

V1, m2 V2,


F = F + F = V		dM	+ V		dM	= -V m + V m			.
F = F + F = V			+ V			= -V m + V m			.
p p1 p2	1 dt			2 dt		1 1	2	2
,	m1=m2=m0,			Fp=m0(V2-V1).			,

“ ” m0, .

u = v,

V = u v = 0,

= F – .

d(Mv)

u = 0,

V = v,

= F - v

Þ M

+ v

= F

F = F =0, M

= V

= F – .

(F=0 – )

(V=const)

( ) :

M	dv	= -V	dM	.	(5)
	dt
			dt

0, v0,

– v,

(5)

Dv=v–v0 – (1903 ,

1857-1935):

dv = -V

, òdv = -V ò

= -V

(ln M - ln M0 )

v−v0

−

v = v0 + V ln

M = M0e


= -V ln				M
= -V ln				M0
				M0
	M0	= e		v
	M0		V		.	(4)
			V		.	(4)
	M

, v

0 V

( – F=Mg), V=u-v=u,

v=0 ( ).

, 0/ ,–

: V » (3-5) , 0/ » 10-20. ,

: v =4×ln15 » (4×2,3×lg15) » 4×2,71 » 10,8 ,

(v » 12 ), .

v » 7

v » 8 .

. . ,

: (

. v = V×ln(M0/M)

x(t) = x0 +V òln M0 dt . M(t)

). :

(t) = 0(1-at) (t) = 0 -αt ,

									9
a – “ ” 0.

	120						,
	100						,
0							,
	80						,
	80						0 ( 0 ),
	60						0 ( 0 ),
	60						.
	40						.
	40						(4), 0
	20						(4), 0
							:
	0	4	8	12	16	20	24	v
	0	4	8	12	16	20	24	M0 = M eV	( v0 = 0).
		,						M0 = M eV	( v0 = 0).

. 1	. 1
			V=5 .
, ,	v = 24	120

( )!

, !

? , ,

V=5-7 , . ,

v=100 , 0/ = 490×106.

= 1000 = 1 , !

v~ ,

=f(v)

( : 0 = » 6×1021 , = 1 V = 5 ,

v = 251 !!! ? – !)

. t t+dt

Mdv,

, V, V –

. ,

F, dt Fdt. :

Mdv = Fdt ± dmV ,

„+” – ; „-” – .

, ± dM . :

dM = + , dM = – . :

M dv = F + dM V , dt dt

V – .

10. .

. .

. , . 1- , 2- 3- .

§1. .

“ ” (

, ).

: “ ,

, , – ,

, , ,

”.

. – :

. ,

– , .

XVI . , ,

(

!).

. (1571-1630 .),

(1546-1601 .) , 1609

1),

2),

(

)

ö2

ö3

ç T1

ç a1

= K ,

K = G

( ç

= ç

)

(1)

T 2

4p2

è 2

– ( , – ).

1- 2- .

“ ”

, , , , =0.

v =0

( ) –

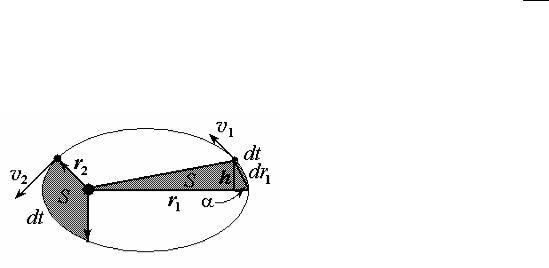
F12 i F21, , ,

, ( ),

, =0. dN = 0 , , dt

N=const. N=[r×p]=m×[r×v]


	–
: . 1- .
		: ,
	,
	( . 1).
	N=const, N1=N2
	t1 i t2;		N1=(mv×r×sina)1 =
	m×(dr/dt)×r×sina = m×r×(dr×sina)/dt = m×r×h/dt
	= (m2S/dt)1. : N2 = (m2S/dt)1.
. 1	dt1=dt2, , S1=S2,

, 2-

( , sina = sin(180-a)).

: ,

16 , 1686 ,

, . ,

, ,

( ).

F = G	m1m2	.	(2)

	r 2

G=(6,672±0,003)×10-11 × 2 2 – , ,

1 1

. G (1731-1810 .) 1798 , 1898 .

, (2)

(“

”), , r – .

, ,

, (2)

F = åFij = Gåå	Dmi Dm j æ r ö			,	(2 )
		ç	÷
	r 2
i j		è r ø		ij
	ij

D D j – , rij – , r/r –

, , .

, ,

( ) ,

, F=0 ( F=0

)

, .

F = k	q1q2		r	,	( k =	1	)	(3)
	r 2		r			4pee0

k = 9×109 × 2 2 ( , e=1), q1 i q2 – , r –

. k, F,

, (

e).

, –

, .

, , ,

, , , .

, ,

. , » 104 1

F»6×10-3 ,

. ,

, .

( r) ,

( ),

, , .

, .

( ).

( )

§2.

g =

= -G

m r

( E =

= k

) , (4)

r2 r

1 – , F, 2 – , . g –

, – ,

( =1 , “ ” )

. 1

h ( ) ( 2= , r=R +h):

F = G	m1M3	r	= m1 g .
	(R3 + h)2	r

, g = F/m h (h=0)

, , ) :

= -G

M r

= G

= 6,672 ×10

−11 5,98

×1024

» 9,83 (

R2 r

(6,371×106 )2

(

) :

g × dr =

gdr =

= - G

( j

= k

(5)

r 2

( F || dr, >0).

( ) ,

. –

, .

( ). (2) 1 2 –

, , 1894

10-9), 1971 , 10-12

: / = 1±10-12.

= , ( ,

)

( m a=F ):

a =

m M3

= G

= g – (6)

r 2 m

r 2

+ h)2

h , 3 R3 – .

(6) .

§3. .

	,
(F=-F ), ( ,
, )		r, (

F dr ):

∞

Mm ö

dA=Fdr A = òG

dr = -G

= -0 - ç

- G

= G

r ø

, ,

( ) ( )

, U(¥)=0,

DU = A ®U(¥) - U(r) = -U(r) = G	Mm	U(r) = -G	Mm	– (7)
	r
			r

. , U(r) = –A ( ,

)

–

j =	U(r)	= -G	M	,	(8)
	m
			r

( =1 ) .


			R ( .2).

	,	.

	,
	, , ,
. 2	,
		.

), , .

r =	M	=	3M	.	(9)

	V 4pR3

( )

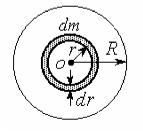
dr, . ( )

, ,

(

dr r

dm = rdV = r×S×dr = r r2dr

(S – ).

, ( .

7):

dA = -Udm = G	M	dm = G	rV	dm	dA = G	r(4pr3 / 3) ×r4pr 2dr	.
	r		r			r

, :

	16p2r R		16p2r		r 5	R	16p2r2		R5

A = G		òr 4dr = G		×		= G		×		.	(10)
	3		3		5		3		5
		0				0

dA ,

, ,

U = – ,

=rV=r R3/3.

= -G

r2 42 p2

= -

r2V 2

= -

M 2

(11)

5 R

, ?

( , ) –

. ,

Mc2 =

GM2

R »

(12)

»6,0×1024 ,

R »

6,7 ×10−11 ×6 ×1024

= 4,5×10−3 ( )

(4,5 !).

×108 )2

. R3»6,4×106 = 6400 ,

, (

). :

R )» 1,5×103 = 1,5 (R »7×108 = 700000 , »2×1030 ), R )» 5×10-6 = 5 (R »1,7×106 = 1700 , »7×1022 ).

<<< < Предыдущая 1 2 3 4 5 67 / 207 8 9 10 11 12 13 14 15 16 17 18 19 20 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
26.11.20193.64 Mб22Metod_stomat_1.doc
#
08.05.20192.38 Mб11metod_z_kh_Ch1.doc
#
02.03.2016329.73 Кб26METROLOGIYa (2).doc
#
02.03.2016610.3 Кб50MEV Book ALL.doc
#
08.09.2019510.46 Кб1mev.doc
#
02.03.20161.71 Mб5MexLekcii2010prn.pdf
#
02.03.2016479.74 Кб17Mikroekonomika_Konspekt.doc
#
02.03.201644.85 Кб6MINISTERSTVO_OSVITI_I_NAUK.docx
#
02.03.201625.87 Кб16Ministerstvo_osviti_i_nauki.docx
#
02.03.2016665.09 Кб16Mizhnarodna_informatsiya_Lektsiyi.doc
#
08.12.2018730.11 Кб5Mizhnarodna_informatsiya_Lektsiyi.doc