
- •Навчальна програма
- •Навчальна програма Семестр перший. Аналітична геометрія Модуль 1
- •Модуль 2
- •Література
- •Питання, що виносяться на модуль 1
- •Питання, що виносяться на модуль 2
- •Типові приклади і задачі до модулю 1
- •Типові приклади і задачі до модулю 2
- •Семестр другий. Вища алгебра Модуль 3
- •Модуль 4
- •Питання, що виносяться на модуль 3
- •Питання, що виносяться на модуль 4
- •Література
- •Питання, що виносяться на модуль 3
- •Питання, що виносяться на модуль 4
- •Таблиця залікових рейтингових балів та оцінок
- •Таблиця відповідності модульних рейтингових оцінок в балах та за існуючою національною шкалою
Питання, що виносяться на модуль 3
Обчислити детермінанти
![]() ,
,
 ,
, ,
, ,
,
 ,
,
 ,
, .
.
Користуючись теоремою Лапласа, обчислити детермінанти
 ,
,
 ,
, .
.
Розв’язати матричні рівняння
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
Знайти обернену матрицю до матриці
 ,
,
 ,
, ,
,
 ,
,
 ,
, .
.
Розв’язати систему рівнянь



За правилом Крамера розв’язати систему рівнянь
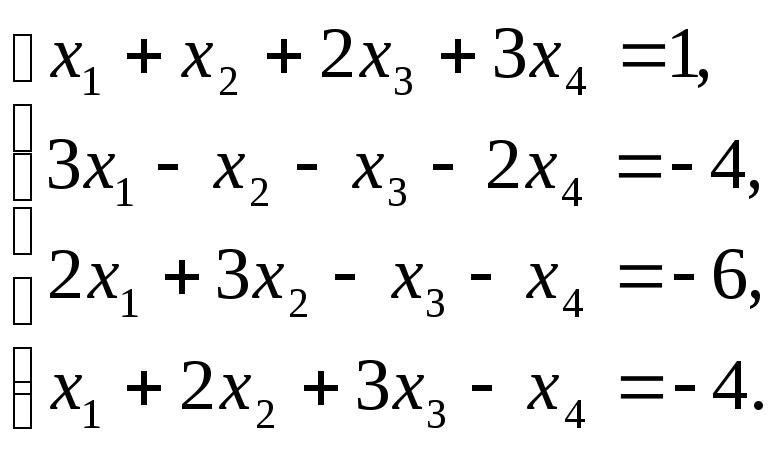
За методом Гауса розв’язати систему рівнянь
а)
 б)
б)
Дослідити сумісність, знайти загальний і один частинний розв’язок системи рівнянь
а)
 б)
б)
Знайти загальний розв’язок та фундаментальну систему розв’язків системи однорідних лінійних рівнянь
а)
 б)
б)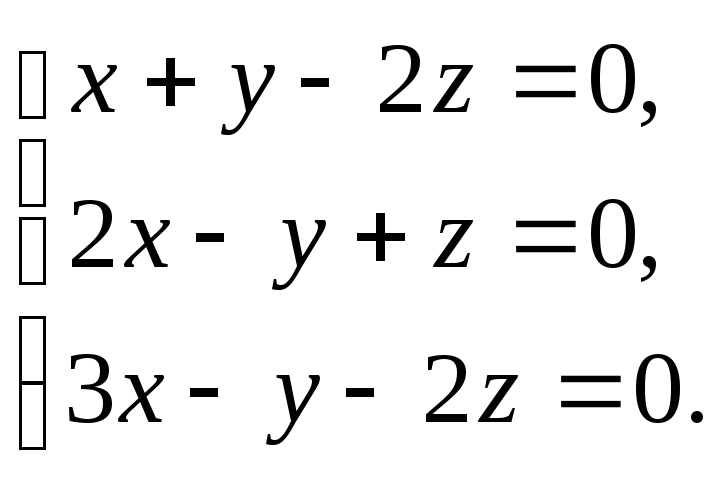
в)
 г)
г) д)
д)
Питання, що виносяться на модуль 4
Довести, що система векторів
 є базою простору
є базою простору .
Знайти координати вектора
.
Знайти координати вектора в цій базі:
в цій базі:
![]()
Довести, що системи векторів
 та
та утворюють бази в
утворюють бази в .
Знайти матрицю переходу та формули
перетворення координат при переході
від першої до другої бази. Знайти
координати вектора
.
Знайти матрицю переходу та формули
перетворення координат при переході
від першої до другої бази. Знайти
координати вектора в обох базах, якщо:
в обох базах, якщо:
![]()
Відображення
 переводить кожен вектор
переводить кожен вектор у вектор
у вектор .
Довести, щоfє
лінійним оператором. Знайти матриці
цього оператора в канонічній базі
.
Довести, щоfє
лінійним оператором. Знайти матриці
цього оператора в канонічній базі
 та в базі
та в базі ,
та образи векторів цієї бази, якщо
,
та образи векторів цієї бази, якщо .
.Вияснити, чи являється оператор φ лінійним, у випадку лінійності знайти матрицю оператора в тій же базі, в якій задані координати векторів х і φх
![]()
Побудувати лінійний оператор
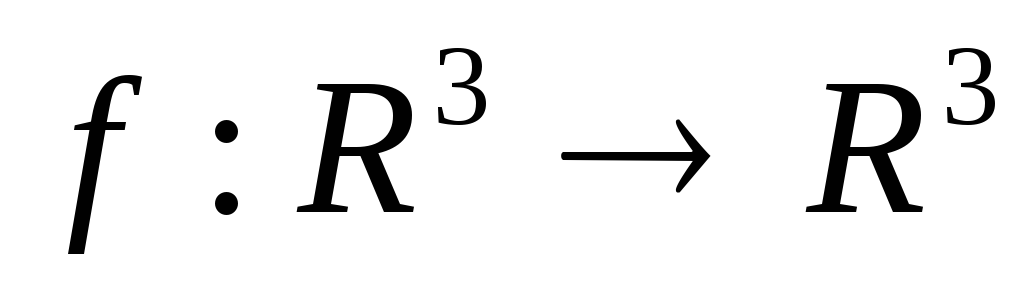 ,
що переводить базу
,
що переводить базу ,
, у вектори
у вектори
 .
Знайти матрицю оператораfв базі
.
Знайти матрицю оператораfв базі
 .
.Оператор φ в базі
 має матрицю
має матрицю
 ,
а операторψ
в базі
,
а операторψ
в базі
 має матрицю
має матрицю .
Знайти матрицюφ
+ ψ
оператора в базі
.
Знайти матрицюφ
+ ψ
оператора в базі

Нехай лінійний оператор
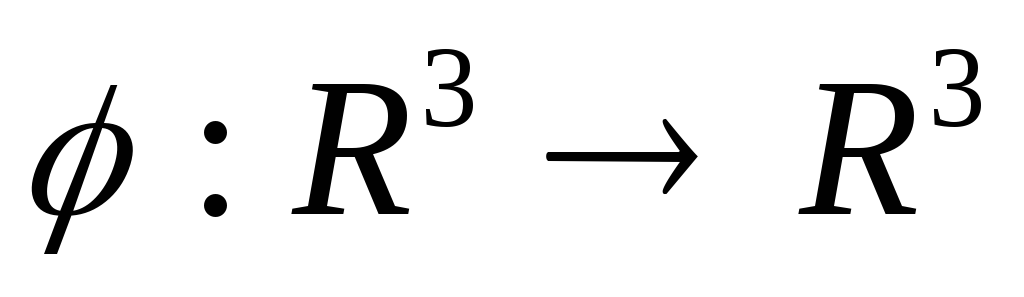 переводить вектор
переводить вектор у вектор
у вектор ,
, - матриця оператора
в базі
- матриця оператора
в базі
 .
Знайти матриці операторів
.
Знайти матриці операторів та
та в канонічній базі простору
в канонічній базі простору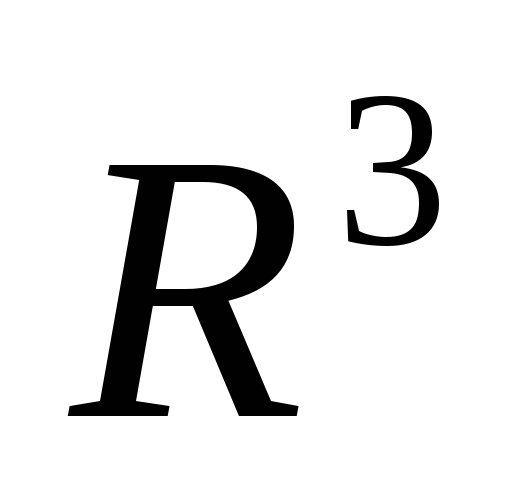 ,
якщо
,
якщо
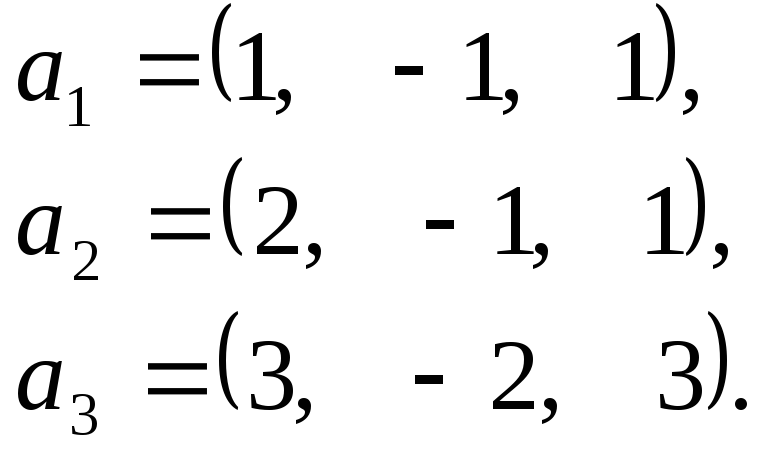

Лінійний оператор φ в базі
 має матрицю
має матрицю
 .
Знайти
матрицю цього ж оператора в базі
.
Знайти
матрицю цього ж оператора в базі
 .
.Знайти власні значення та власні вектори лінійного оператора, заданого в деякій базі матрицею:
а)
 , б)
, б)
Нехай
 ,
,
 ,
, –
–
матриці лінійних операторів
![]() відповідно в канонічній базі простору
відповідно в канонічній базі простору![]() .
Довести, що в просторі
.
Довести, що в просторі![]() є дві бази, що складаються з власних
векторів операторів
є дві бази, що складаються з власних
векторів операторів![]() і
і![]() в цих базах. Довести, що в
в цих базах. Довести, що в![]() немає бази, що складається з власних
векторів оператора
немає бази, що складається з власних
векторів оператора![]() .
.
Вияснити, чи можна звести матрицю лінійного оператора до діагонального вигляду шляхом переходу до нової бази. Знайти цю базу і відповідну їй матрицю:

Застосовуючи процес ортогоналізації побудувати ортогональну базу підпростору, натягнутого на дану систему векторів:
а)
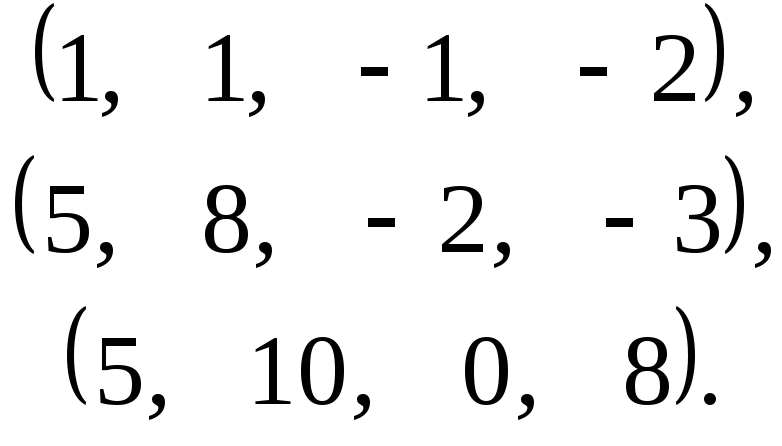 б)
б) в)
в)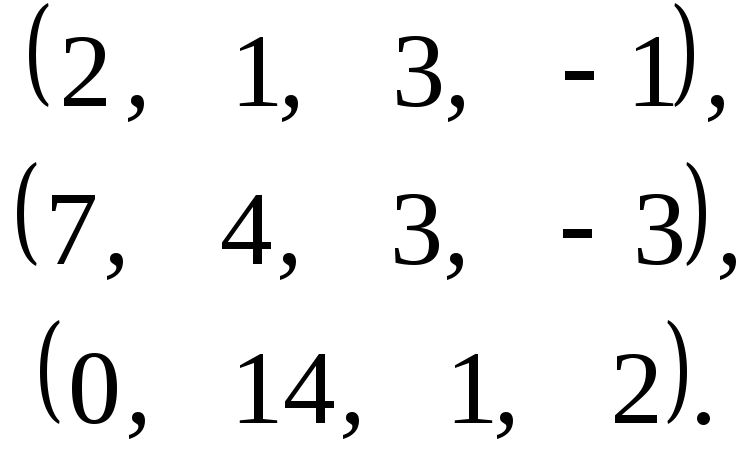
В евклідовому просторі
 ортонормувати систему векторів
ортонормувати систему векторів
![]()
Звести до канонічного вигляду квадратичні форми
![]() ;
; ![]() .
.
Чи будуть додатньо визначеними квадратичні форми
![]() ;
; ![]() .
.
Звести до головних осей квадратичні форми
![]() ;
; ![]() .
.
Визначити тип поверхні, заданої рівнянням
 та знайти її канонічне рівняння
та знайти її канонічне рівняння
а)
![]() ;
;
б)
![]() .
.
Викладачі:лектор доцент Кирилюк О.А., викладач практичних занять: асп. Кіндюх С. П.
Метод навчання:Лекції та практичні заняття
Передумова:Необхідні загальні знання з основ алгебри та геометрії, а також базові шкільні знання з математики
-
Оцінка
Бали
Відмінно
85-100
Добре
65-84
Задовільно
50-64
Незадовільно з можливістю повторного перескладання
30-49
Незадовільно з повторним прослуховуванням курсу
1-29
Таблиця відповідності модульних рейтингових оцінок в балах та за шкалою ECTS
-
Оцінка ECTS
Оцінка
Бали
A
Відмінно
85-100
B
Дуже добре
75-84
C
Добре
65-74
D
Задовільно
58-64
E
Достатньо
50-57
FX
Незадовільно з можливістю повторного перескладання
30-49
F
Незадовільно з повторним прослуховуванням курсу
1-29
Залікова методика:письмовий залік (для тих, хто за результатами роботи в семестрі має на це право). Залікова оцінка визначається в залежності від кількості балів, набраних студентом протягом семестру з контрольні роботи, індивідуальну роботу та виконання робіт
