Линии напряженности
Электрическое поле не действует на органы чувств. Его мы не видим. Тем не менее распределение поля в пространстве можно сделать видимым. Английский физик Майкл Фарадей в 1845 году предложил изображать электрическое поле с помощью силовых линий и получал своеобразные карты, или диаграммы поля.
-
Силовая линия (или линия напряженности) — это воображаемая направленная линия в пространстве, касательная к которой в каждой точке совпадают с направлением вектора напряженности в этой точке (рис. 5).
|
Рис. 5 |
Рис. 6 |
По картине силовых линий можно судить не только о направлении вектора, но и о его значении. Действительно, для точечных зарядов напряженность поля увеличивается по мере приближения к заряду, а силовые линии при этом сгущаются (рис. 6). Где силовые линии гуще, там напряженность больше и наоборот.
-
Число силовых линий, приходящихся на поверхность единичной площади, расположенную нормально к силовым линиям, пропорционально модулю напряженности.
Картины силовых линий
Построить
точную картину силовых линий заряженного
тела – сложная задача. Нужно сначала
вычислить напряженность поля Е(х,
у, z) как функцию
координат. Но этого еще мало. Остается
непростая задача проведения непрерывных
линий так, чтобы в каждой точке линии
касательная к ней совпадала с направлением
напряженности
![]() .
Такую задачу проще всего поручить
компьютеру, работающему по специальной
программе.
.
Такую задачу проще всего поручить
компьютеру, работающему по специальной
программе.
Впрочем, строить точную картину распределения силовых линий не всегда необходимо. Иногда достаточно рисовать приближенные картины, не забывая что:
-
силовые линии — это незамкнутые линии: они начинаются на поверхности положительно заряженных тел (или в бесконечности) и оканчиваются на поверхности отрицательно заряженных тел (или в бесконечности);
-
силовые линии не пересекаются, так как в каждой точке поля вектор напряженности имеет лишь одно направление;
-
между зарядами силовые линии нигде не прерываются.
На рисунках 7–10 изображены картины силовых линий: положительно заряженного шарика (рис. 7); двух разноименно заряженных шариков (рис. 8); двух одноименно заряженных шариков (рис. 9); двух пластин, заряды которых равны по модулю и противоположны по знаку (рис. 10).
|
Рис. 7 |
Рис. 8 |
|
Рис. 9 |
Рис. 10 |
На рисунке 10 видно, что в пространстве между пластинами вдали от краев пластин силовые линии параллельны: электрическое поле здесь одинаково во всех точках.
-
Электрическое поле, напряженность которого одинакова во всех точках пространства, называется однородным.


Работа при перемещении заряда в однородном электростатическом поле. Однородное поле создают, например, большие параллельные металлические пластины, имеющие заряды противоположного знака. Это поле действует на заряд q с постоянной силой F = qE, подобно тому как Земля действует с постоянной силой F = mg на камень вблизи ее поверхности.
Пусть пластины расположены вертикально (рис. 2), левая пластина заряжена положительно, а правая — отрицательно Вычислим работу, совершаемую полем при перемещении положительного заряда q из точки 1, находящейся на расстоянии dx от левой пластины, в точку 2, расположенную на расстоянии d2 от нее.
Точки 1 и 2 лежат на одной силовой линии:
А = qE (d1 - d2) = qE∆d. (1)
Эта работа не зависит от формы траектории, подобно тому, как не зависит от формы траектории работа силы тяжести.
Потенциальная энергия. Поскольку работа электростатической силы не зависит от формы траектории точки ее приложения, эта сила является консервативной, и ее работа согласно формуле равна изменению потенциальной энергии, взятому с противоположным знаком:
A = -(Wn2-Wnl) = -∆Wn.
Сравнивая полученное выражение с общим определением потенциальной энергии, видим, что потенциальная энергия заряда в однородном электростатическом поле равна:
Wn = qEd.
Если поле совершает положительную работу, то потенциальная энергия заряженного тела в поле уменьшается: ∆Wn < О. Одновременно согласно закону сохранения энергии растет его кинетическая энергия. И наоборот, если работа отрицательна (например, при движении положительно заряженной частицы в направлении, противоположном направлению вектора напряженности поля Е, то ∆Wn > 0. Потенциальная энергия растет, а кинетическая энергия уменьшается, частица тормозится.
На замкнутой траектории, когда заряд возвращается в начальную точку, работа поля равна нулю:
A = -∆Wn = -(Wnl - Wn2) = 0.
Заряженные частицы в электростатическом поле обладают потенциальной энергией. При перемещении частицы из одной точки поля в другую электрическое поле совершает работу, не зависящую от формы траектории. Эта работа равна изменению потенциальной энергии, взятой со знаком «—».
В механике взаимное действие тел друг на друга характеризуют силой и потенциальной энергией. Электростатическое поле, осуществляющее взаимодействие между зарядами, также характеризуют двумя величинами. Напряженность поля — это силовая характеристика. Теперь введем энергетическую характеристику — потенциал.
Потенциал поля. Работа любого электростатического поля при перемещении в нем заряженного тела из одной точки в другую также не зависит от формы траектории, как и работа однородного поля. На замкнутой траектории работа электростатического поля всегда равна нулю. Поля, обладающие таким свойством, называют потенциальными. Потенциальный характер, в частности, имеет электростатическое поле точечного заряда.
Работу потенциального поля можно выразить через изменение потенциальной энергии. Формула А = — (Wn2 — Wnl) справедлива для любого электростатического поля. Но только в случае однородного поля потенциальная энергия выражается формулой.
Потенциал. Потенциальная энергия заряда в электростатическом поле пропорциональна заряду. Это справедливо как для однородного поля, так и для неоднородного. Следовательно, отношение потенциальной энергии к заряду не зависит от помещенного в поле заряда.
Это позволяет ввести новую количественную характеристику поля — потенциал φ, не зависящую от заряда, помещенного в поле.
Для определения значения потенциальной энергии, как мы знаем, необходимо выбрать нулевой уровень ее отсчета. При определении потенциала поля, созданного системой зарядов, предполагается, что потенциал в бесконечно удаленной точке поля равен нулю.
Потенциалом точки электростатического поля называют отношение потенциальной энергии заряда, помещенного в данную точку, к этому заряду.
Согласно данному определению потенциал равен:

Напряженность поля Е — векторная величина. Она представляет собой силовую характеристику поля, которая определяет силу, действующую на заряд q в данной точке поля. А потенциал φ — скаляр, это энергетическая характеристика поля, он определяет потенциальную энергию заряда q в данной точке поля.
Если в примере с двумя заряженными пластинами в качестве точки с нулевым потенциалом выбрать точку на отрицательно заряженной пластине, то согласно формулам потенциал однородного поля равен:

Разность потенциалов. Подобно потенциальной энергии, значение потенциала в данной точке зависит от выбора нулевого уровня для отсчета потенциала, т. е. от выбора точки, потенциал которой принимается равным нулю. Изменение потенциала не зависит от выбора нулевого уровня отсчета потенциала.
Так
как потенциальная энергия
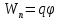 ,
то работа сил поля равна:
,
то работа сил поля равна:

Здесь
 —
разность потенциалов, т. е. разность
значений потенциала в начальной и
конечной точках траектории.
—
разность потенциалов, т. е. разность
значений потенциала в начальной и
конечной точках траектории.
Разность потенциалов называют также напряжением.
Согласно формулам разность потенциалов между двумя точками оказывается равной:

Разность потенциалов (напряжение) между двумя точками равна отношению работы поля при перемещении положительного заряда из начальной точки в конечную к величине этого заряда.
Если за нулевой уровень отсчета потенциала принять потенциал бесконечно удаленной точки поля, то потенциал в данной точке равен отношению работы электростатических сил по перемещению положительного заряда из данной точки в бесконечность к этому заряду.
Единица разности потенциалов. Единицу разности потенциалов устанавливают с помощью формулы. В Международной системе единиц работу выражают в джоулях, а заряд — в кулонах. Поэтому разность потенциалов между двумя точками численно равна единице, если при перемещении заряда в 1 Кл из одной точки в другую электрическое поле совершает работу в 1 Дж. Эту единицу называют вольтом (В); 1 В = 1 Дж/1 Кл.