Прикладсортування елементів масиву у зростаючому порядку за методом обміну
На рисунках 8.9– 8.13детально показані зміни масиву в процесі сортування обміном під час першого проходу.
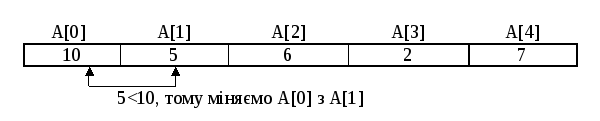
Рисунок 8.9–Масив до сортування
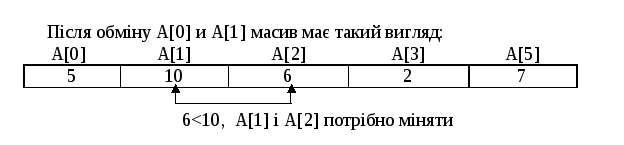
Рисунок 8.10– Масив післе першого обміну елементів
Рисунок 8.11 – Масив після другого обміну елементів
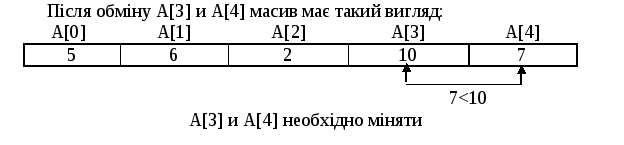
Рисунок 8.12 – Масив після третього обміну елементів
Рисунок 8.13 – Масив після першого проходу
Після першого проходу максимальний елемент став на своє місце у кінці масиву, тому в другому проході по масиву цей елемент уже аналізуватися не буде, тобто число порівнянь в другому проході буде на одне менше.
Другий прохід по масиву розглянемо менш детально. Його результати представлені на рисунку 8.14.
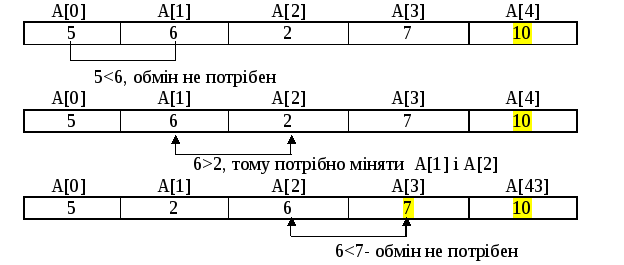
Рисунок 8.14 – Другий прохід по масиву
У другому проході знадобився лише один обмін, і в результаті не тільки A[3], але й A [2] виявилися на своїх місцях.
Результати останнього проходу по масиву показані на рисунку 8.15.
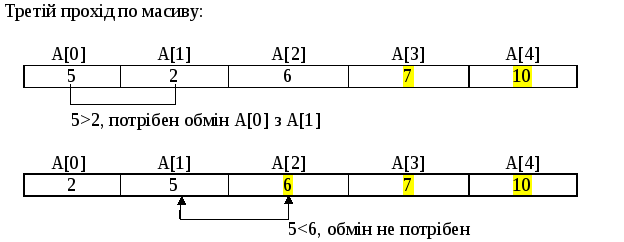
Рисунок 8.15 – Результати третього проходу по масиву
Після третього проходу всі елементи опинилися на своїх місцях. У загальному випадку для сортування масиву знадобився б ще один прохід, але у даному випадку сортування вже закінчено. У цьому особливість сортування обміном – число проходів може бути менше максимально можливого.
Функція сортування масиву методом обміну
Функція, представлена на рисунку 8.16 реалізує за допомогою циклів for алгоритм, зображений на рисунку 8.1.
Рисунок 8.16 - Функція сортування елементів масиву у зростаючому порядку за методом обміну
Роботу функції, представленої на рисунку 8.16 можна прискорити, якщо після обміну елементів фіксувати номер елементу, що останнім змінювався (значення змінної і). Це значення можна використовувати і як ознаку завершення сортування, так і в якості максимального значення параметру внутрішнього циклу. Це удосконалення алгоритму дозволяє дещо зменшити кількість циклів сортування. Саме такий спосіб слід реалізувати у проекті до лабораторної роботи.
Сортування вставкою
Суть алгоритму полягає у наступному. На кожному кроці елементи масиву поділені на впорядковану частину А[1], А[2], ......, А[i-1], яка розташовується на початку масиву, та невпорядковану частину А [i], ....... , а [N], і перший елемент з невпорядкованої частини вставляється в упорядковану. На початку сортування впорядкована частина складається всього з одного, першого елемента, а всі інші елементи розташовуються в другій частині масиву. Схема цього алгоритму наведена на рисунку 8.17,
Послідовні кроки алгоритму сортування полягають у тому, що перший елемент з невпорядкованої частини порівнюється з останнім елементом впорядкованої послідовності. Якщо виявляється, що порядок розташування цих елементів не відповідає вимогам сортування, то елемент з невпорядкованої частини вилучається і переноситься в упорядковану частину. Місце для цього елементу звільняється шляхом зсуву упорядкованих елементів вправо на місце витягнутого елемента. Зсув упорядкованих елементів на одну позицію вправо триває, поки не буде знайдено місце для елемента, вилученого з невпорядкованої послідовності.
Як видно з рисунку 8.17, в алгоритмі є два цикли.
У зовнішньому циклі послідовно змінюється номер лівої межі невпорядкованою області від другого елементу (i=1) до кінця масиву. У тілі цього циклу порівнюються елементи, що знаходяться по обидва боки від межі, що розділяє впорядковану і невпорядковану частини. Якщо порядок порушений, то перший елемент невпорядкованою послідовності запам'ятовується у змінній tmp, внаслідок чого звільняється місце для зсувів упорядкованих елементів вправо.
Внутрішній цикл забезпечує послідовні зсуви упорядкованих елементів вправо, починаючи з останнього, доти, поки не буде знайдено місце для першого елемента з невпорядкованою області, що зберігався у змінній tmp.
Можливість вставки елементу визначається однією з двох умов.
(mas[j-1] <= buf < mas[j] ),якщо (1 < j < i ), тобто знайдено місце всередині впорядкованої послідовності.
j=1 , тобто. tmp менше ніж усі елементи впорядкованої частини і має бути поставлений на перше місце у впорядкованій частині масиву.
Після виконання однієї з цих умов цикл зсувів завершується і елемент масиву із змінної tmp переноситься на знайдене місце у впорядкованій послідовності.
Рисунок 8.17-Алгоритм сортування елементів масиву у зростаючому порядку за методомвставки