
m0097 / ГИА-2013. Математика. Тренировочн. раб. 1 (вар. 1-4) 04.12.2012г. (с ответами)
.pdf
Тренировочная работа1 №
по МАТЕМАТИКЕ
4 декабря 2012 года
9 класс
Вариант 1
Район Город (населённый пункт) Школа Класс Фамилия Имя Отчество
Математика1. 9 классВариант. |
2 |
Инструкция по выполнению работы
Общее время экзамена 4 часа (240 минут)
Всего в работе 26 заданий, из которых 20 заданий базового уровня (часть I) 6и
заданий повышенногоуровня (часть II) |
|
|
|
|
||
Работа состоит:из« трёхГемо»,дулейметрия« |
Алгебра |
Реальная», « |
математика». |
|||
Модуль» |
«Алгебра содержит 11 заданий: в части I — 8 |
заданий с кратким ответом, |
||||
выбором ответа и установлением соответствия; в |
части |
II — 3 |
задания с |
полным |
||
решением |
|
|
|
|
|
|
Модуль «Геометрия» содержит 8 заданий: в части I — 5 |
заданий с кратким ответом, |
|||||
в части II — 3 задания с полным решением |
|
|
|
|
||
Модуль «Реальная математика» |
содержит 7 заданий: все задания — в части I, с |
|||||
кратким ответом и выбором ответа |
|
|
|
|
|
|
Сначала |
выполняйте задания части I. Начать |
советуем с, того модуля |
задания |
|||
которого вызывают у Вас меньше затруднений, затем переходите к другим модулям Для экономии времени пропускайте задание, которое не удаётся выполнить, сразу и переходите к следующему Если у Вас останется время, Вы сможете вернуться к пропущенным заданиям
Все необходимые вычисления, преобразования и. т. д выполняйте в черновике. Если задание содержит рисунок, то на нём можно выполнять необходимые Вам построения. Обращаем Ваше внимание на то, что записи в черновике не будут учитываться при оценивании работы Рекомендуем внимательно читать условие и проводить проверку полученногоответа
При выполнении заданий с выбором ответа обведите номер выбранного ответа в экзаменационной работе. Если Вы обвели не, тот номер то зачеркните обведённый номер крестиком и затем обведите номер правильного ответа
Если варианты ответа к заданию, не приводятся полученный ответ записывается в отведённом для этого месте. В случае записи неверного ответа зачеркните его и запишите рядом новый. Наименования указывать не надо. Если в ответе надо записать несколько чиселпишите, их через точку с запятойнапример, : –1;7
Если в задании требуется установить соответствие между некоторыми объектами, впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру
Решения заданий части II и ответы к ним записываются на отдельном. |
листе |
Текст |
|
задания можно не переписыватьнеобходимо, |
лишь указать его номер |
|
|
Баллы, полученные Вами за верно |
выполненные. задания, суммируются |
Для |
|
успешного прохождения итоговой аттестации необходимо набрать в сумме не менее 8 баллов, набранные по всей работе, из них не менее 3-х баллов по модулю «Алгебра», 2-х баллов по модулю «Геометрия»2и- х баллов по модулю «Реальная математика»
Желаем успеха!
© МИОО 2012 г
Ɇɚɬɟɦɚɬɢɤɚ. 9 ɤɥɚɫɫ. ȼɚɪɢɚɧɬ 1 |
Ɇɚɬɟɦɚɬɢɤɚ. 9 ɤɥɚɫɫ. ȼɚɪɢɚɧɬ 1 |
4 |
ɑ ɫɬɶ 1 |
5 |
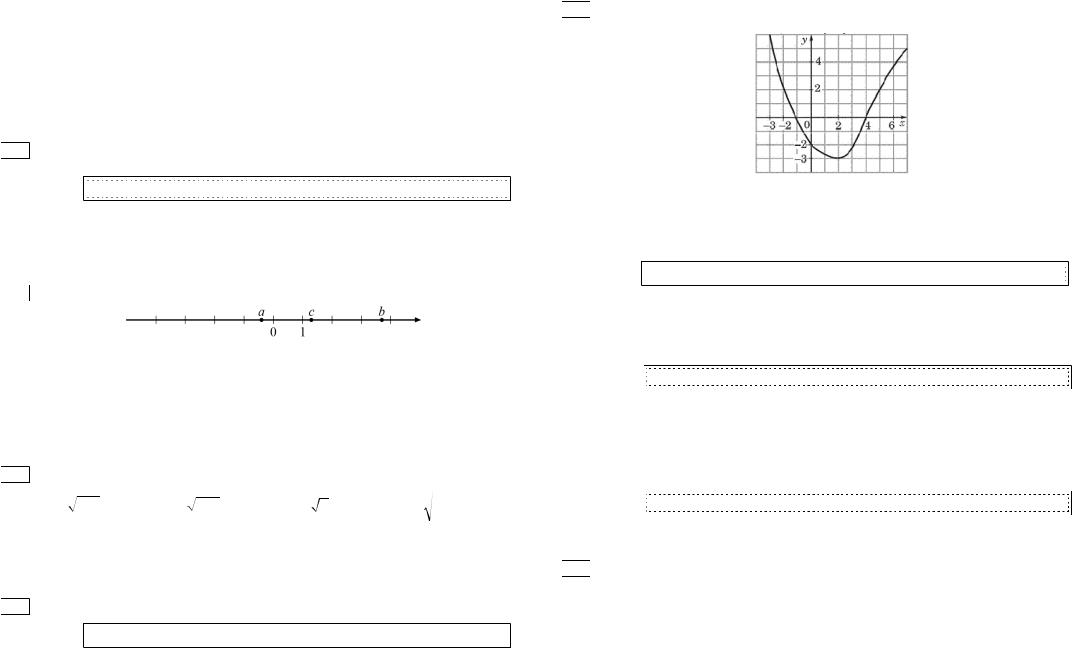
ɇɚ ɪɢɫɭɧɤɟ |
ɢɡɨɛɪɚɠɺɧ ɝɪɚɮɢɤ ɮɭɧɤɰɢɢ. |
y f (x) Ʉɚɤɢɟ ɢɡ ɭɬɜɟɪɠɞɟɧɢɣ |
|
Ɇɨɞɭɥɶ «Ⱥɥɝɟ ɪ |
|
ɨɬɧɨɫɢɬɟɥɶɧɨ |
ɷɬɨɣ ɮɭɧɤɰɢɢ? |
ɧɟɜɟɪɧɵ ɍɤɚɠɢɬɟ ɢɯ ɧɨɦɟɪɚ. |
|
» |
|
|
|
|
|
1 ɇɚɣɞɢɬɟ: ɡɧɚɱɟɧɢɟ ɜɵɪɚɠɟɧɢɹ 15 |
1 |
2 9 |
2 |
2. |
|
|
|
3 |
|
|
|||
2 |
|
|
ɮɭɧɤɰɢɹ ɜɨɡɪɚɫɬɚɟɬ ɧɚ ɩɪɨɦɟɠɭɬɤɟ [ 2; f) |
|||
Ɉɬɜɟɬ: |
|
|
1) |
|||
|
|
|
|
2) |
f (3) |
! f ( 3) |
|
|
|
|
3) |
f (0) |
2 |
|
|
|
|
4) |
ɩɪɹɦɚɹ y 2 ɩɟɪɟɫɟɤɚɟɬ ɝɪɚɮɢɤ ɜ ɬɨɱɤɚɯ ( 2; 2) ɢ (5; 2) |
|
Ɉɬɜɟɬ: 













2ɇɚ ɤɨɨɪɞɢɧɚɬɧɨɣ ɩɪɹɦɨɣ ɨɬɦɟɱɟɧɵ, , ɱɢɫɥɚ. a b c
Ʉɚɤɨɟ ɢɡ ɫɥɟɞɭɸɳɢɯ ɭɬɜɟɪɠɞɟɧɢɣ ɧɟɜɟ?ɪɧɨ |
6 |
ɇɢɤɨɥɚɣ ɫɬɚɪɲɟ Ƚɪɢɝɨɪɢɹ4 ɧɚ ɝɨɞɚ, ɚ Ƚɪɢɝɨɪɢɣ ɫɬɚɪɲɟ ɂɥɶɢ1,5ɜ |
ɪɚɡɚ. ȼɦɟɫɬɟ |
|||||||||||||||
|
|
|
ɢɦ 36 ɥɟɬ. ɋɤɨɥɶɤɨ ɥɟɬ ɂɥɶɟ? |
|
|
|
|
|
|
|||||||||
1) a b ! c |
2) ab c |
|
1 |
! 1 |
4) c a b |
|
|
|
|
|
|
|||||||
3) |
Ɉɬɜɟɬ: |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
7 |
ɉɪɟɞɫɬɚɜɶɬɟ ɜ ɜɢɞɟ ɞɪɨɛɢ ɜɵɪɚɠɟɧɢɟ |
15x2 |
5x ɢ ɧɚɣɞɢɬɟ ɟɝɨ ɡɧɚɱɟɧɢɟ ɩɪɢ |
|||||||||
3 Ʉɚɤɨɟ ɢɡ ɞɚɧɧɵɯ ɱɢɫɟɥ?ɹɜɥɹɟɬɫɹ ɢɪɪɚɰɢɨɧɚɥɶɧɵɦ |
3x 2 |
|||||||||||||||||
|
|
|
x 0, 5. ȼ ɨɬɜɟɬ ɡɚɩɢɲɢɬɟ ɩɨɥɭɱɟɧɧɨɟ. |
|
|
|
|
|
||||||||||
|
|
|
ɱɢɫɥɨ |
|
|
|
|
|||||||||||
1) 1, 6 |
2) |
169 |
3) ( 3 )6 |
4) 6 |
1 |
|
Ɉɬɜɟɬ: |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
8 |
Ɋɟɲɢɬɟ ɧɟɪɚɜɟɧɫɬɜɨ 5 4(x 2) 22 x. |
|
|
|
|
|||||||
|
|
25x2 1 |
|
|
|
|
|
|
1) ( 3; f) |
|
2) |
f; |
1 |
|
|
|||
4 ɇɚɣɞɢɬɟ ɤɨɪɧɢ ɭɪɚɜɧɟɧɢɹ. |
|
|
|
|
|
|
|
|
|
|||||||||
0 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|||||
Ɉɬɜɟɬ: |
|
|
|
|
|
|
|
|
3) |
1 |
; f |
|
4) (f; 3) |
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
||
© ɆɂɈɈ 2012 ɝ. |
© ɆɂɈɈ 2012 ɝ. |
Ɇɚɬɟɦɚɬɢɤɚ 9 ɤɥɚɫɫ ȼɚɪɢɚɧɬ 1 |
5 |
Ɇɨɞɭɥɶ «Ƚɟɨɦɟɬɪɢɹ»
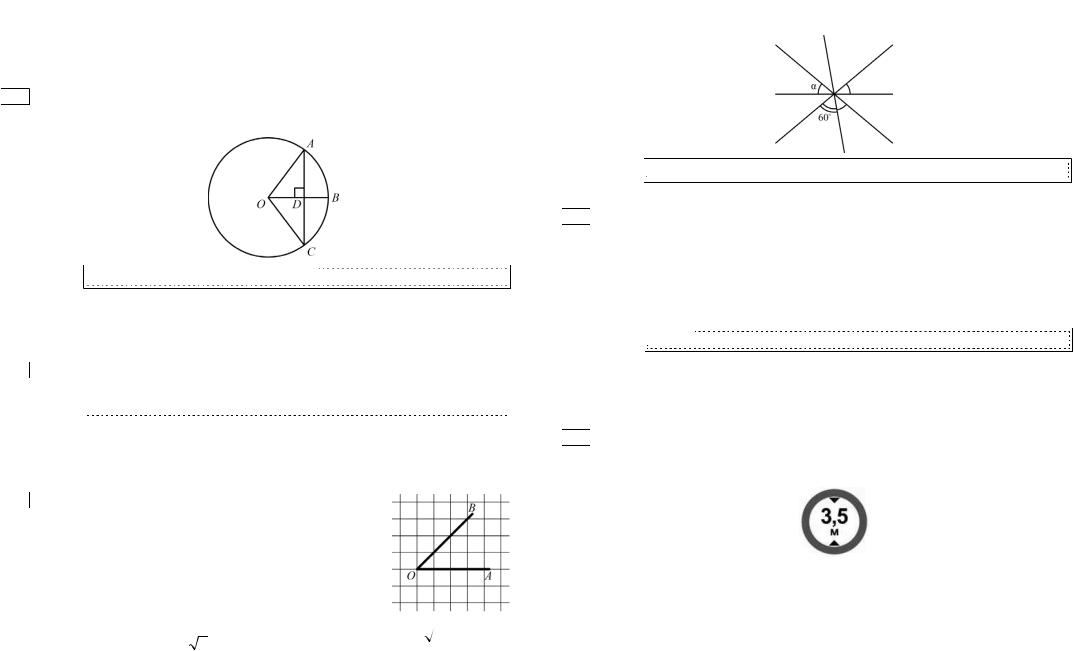
9Ɋɚɞɢɭɫ OB ɨɤɪɭɠɧɨɫɬɢ ɫ ɰɟɧɬɪɨɦ ɜ ɬɨɱɤɟ O ɩɟɪɟɫɟɤɚɟɬ ɯɨɪɞɭ AC ɜ ɬɨɱɤɟ D ɢ
ɩɟɪɩɟɧɞɢɤɭɥɹɪɟɧ ɟɣ. ɇɚɣɞɢɬɟ ɞɥɢɧɭ ɯɨɪɞɵ AC, ɟɫɥɢ BD 2 ɫɦ, ɚ ɪɚɞɢɭɫ ɨɤɪɭɠɧɨɫɬɢ ɪɚɜɟɧ 5 ɫɦ.
Ɉɬɜɟɬ: 





























































10 |
Ɉɫɧɨɜɚɧɢɹ ɬɪɚɩɟɰɢɢ4 |
ɪɚɜɧɵ ɫɦ ɢ 10 ɫɦ. Ⱦɢɚɝɨɧɚɥɶ ɬɪɚɩɟɰɢɢ ɞɟɥɢɬ ɫɪɟɞɧɸɸ |
|
ɥɢɧɢɸ ɧɚ ɞɜɚ ɨɬɪɟɡɤɚ. ɇɚɣɞɢɬɟ ɞɥɢɧɭ ɛɨɥɶɲɟɝɨ ɢɡ ɧɢɯ. |
|
Ɉɬɜɟɬ: 
11 ɑɟɦɭ ɪɚɜɟɧ ɫɢɧɭɫ ɭɝɥɚ AOB?
1) |
1 |
2) |
1 |
3) |
1 |
4) |
2 |
|
2 |
2 |
|||||||
|
|
|
|
|
|
Ɇɚɬɟɦɚɬɢɤɚ 9 ɤɥɚɫɫ ȼɚɪɢɚɧɬ 1 |
|
6 |
12 ɍɝɥɵ, ɨɬɦɟɱɟɧɧɵɟ ɧɚ ɪɢɫɭɧɤɟ ɨɞɧɨɣ, |
ɞɭɝɨɣ. |
ɪɚɜɧɵ ɇɚɣɞɢɬɟ ɭɝɨɥ . Ɉɬɜɟɬ ɞɚɣɬɟ |
ɜ ɝɪɚɞɭɫɚɯ. |
|
|
Ɉɬɜɟɬ: 














































































































13ɍɤɚɠɢɬɟ ɜ ɨɬɜɟɬɟ ɧɨɦɟɪɚ ɜɟɪɧɵɯ ɭɬɜɟɪɠɞɟɧɢɣ.
1)ȿɫɥɢ ɜ ɩɚɪɚɥɥɟɥɨɝɪɚɦɦɟ ɞɢɚɝɨɧɚɥɢ ɪɚɜɧɵ, ɬɨ ɷɬɨɬ ɩɚɪɚɥɥɟɥɨɝɪɚɦɦ – ɩɪɹɦɨɭɝɨɥɶɧɢɤ.
2)ȿɫɥɢ ɩɪɢ ɩɟɪɟɫɟɱɟɧɢɢ ɞɜɭɯ ɩɪɹɦɵɯ ɬɪɟɬɶɟɣ ɧɚɤɪɟɫɬ ɥɟɠɚɳɢɟ ɭɝɥɵ ɪɚɜɧɵ, ɬɨ ɩɪɹɦɵɟ ɩɟɪɩɟɧɞɢɤɭɥɹɪɧɵ.
3)ȿɫɥɢ ɬɪɢ ɭɝɥɚ ɨɞɧɨɝɨ ɬɪɟɭɝɨɥɶɧɢɤɚ ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ ɪɚɜɧɵ ɬɪɺɦ ɭɝɥɚɦ ɞɪɭɝɨɝɨ ɬɪɟɭɝɨɥɶɧɢɤɚ, ɬɨ ɬɚɤɢɟ ɬɪɟɭɝɨɥɶɧɢɤɢ. ɪɚɜɧɵ
Ɉɬɜɟɬ: 












Ɇɨɞɭɥɶ «Ɋɟ ɥɶɧ ɹ ɦ ɬɟɦ ɬɢɤ »
14 Ⱦɨɪɨɠɧɵɣ ɡɧɚɤ, ɢɡɨɛɪɚɠɺɧɧɵɣ ɧɚ«ɪɢɫɭɧɤɟ, ɧɚɡɵɜɚɟɬɫɹ Ɉɝɪɚɧɢɱɟɧɢɟ ɜɵɫɨɬɵ». ȿɝɨ ɭɫɬɚɧɚɜɥɢɜɚɸɬ ɩɟɪɟɞ ɦɨɫɬɚɦɢ, ɬɨɧɧɟɥɹɦɢ ɢ ɩɪɨɱɢɦɢ ɫɨɨɪɭɠɟɧɢɹɦɢ, ɱɬɨɛɵ ɡɚɩɪɟɬɢɬɶ ɩɪɨɟɡɞ ɬɪɚɧɫɩɨɪɬɧɨɝɨ ɫɪɟɞɫɬɜɚ,ɫɝɚɛɚɪɢɬɵ( ɤɨɬɨɪɨɝɨ ɝɪɭɡɨɦ ɢɥɢ ɛɟɡ
) ɝɪɭɡɚ ɩɪɟɜɵɲɚɸɬ ɭɫɬɚɧɨɜɥɟɧɧɭɸ ɜɵɫɨɬɭ.
Ʉɚɤɨɦɭ ɢɡ ɞɚɧɧɵɯ ɬɪɚɧɫɩɨɪɬɧɵɯ ɫɪɟɞɫɬɜ ɷɬɨɬ ɡɧɚɤ ɡɚɩɪɟɳɚɟɬ ɩɪɨɟɡɞ?
1) |
ɦɨɥɨɤɨɜɨɡɭ3770 ɜɵɫɨɬɨɣ |
ɦɦ |
|
2) |
ɩɨɠɚɪɧɨɦɭ ɚɜɬɨɦɨɛɢɥɸ3400 |
ɜɵɫɨɬɨɣ |
ɦɦ |
3) |
ɚɜɬɨɬɨɩɥɢɜɨɡɚɩɪɚɜɳɢɤɭ2900 |
ɜɵɫɨɬɨɣ |
ɦɦ |
4) |
ɚɜɬɨɰɢɫɬɟ3350ɪɧɟ ɜɵɫɨɬɨɣ |
ɦɦ |
|
© ɆɂɈɈ 2012 ɝ |
© ɆɂɈɈ 2012 ɝ |
Ɇɚɬɟɦɚɬɢɤɚ. 9 ɤɥɚɫɫ. ȼɚɪɢɚɧɬ 1 |
7 |
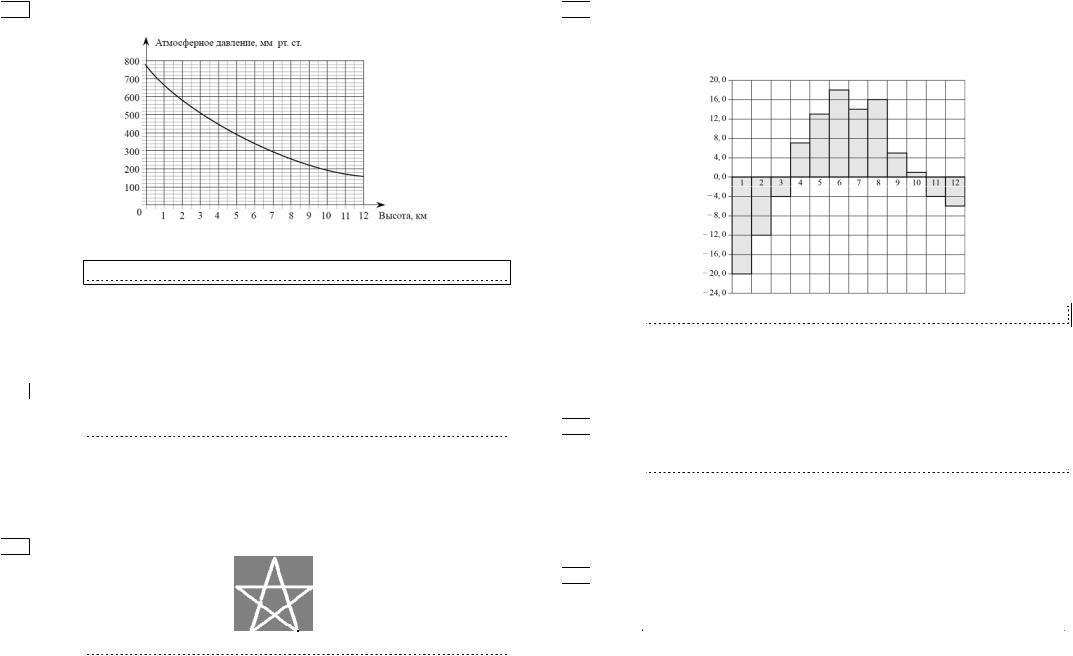
15ɇɚ ɝɪɚɮɢɤɟ ɢɡɨɛɪɚɠɟɧɚ ɡɚɜɢɫɢɦɨɫɬɶ ɚɬɦɨɫɮɟɪɧɨɝɨ( ɞɚɜɥɟɧɢɹ ɜ ɦɢɥɥɢɦɟɬɪɚɯ ɪɬɭɬɧɨɝɨ ɫɬɨɥɛɚ) ɨɬ ɜɵɫɨɬɵ ɧɚɞ ɭɪɨɜɧɟɦ ɦɨɪɹ (ɜ ɤɦ).
ɇɚ ɫɤɨɥɶɤɨ ɦɢɥɥɢɦɟɬɪɨɜ ɪɬɭɬɧɨɝɨ ɫɬɨɥɛɚ ɨɬɥɢɱɚɟɬɫɹ ɞɚɜɥɟɧɢɟ1 ɧɚ ɜɵɫɨɬɟ ɤɦ |
|
ɨɬ ɞɚɜɥɟɧɢɹ6 |
ɧɚ ɜɵɫɨɬɟ ɤɦ? |
Ɉɬɜɟɬ: 











































































































16ɉɥɚɬɚ ɡɚ ɤɨɦɦɭɧɚɥɶɧɵɟ ɭɫɥɭɝɢ ɫɨɫɬɚɜɥɹɥɚ 800. ɪ ɋɤɨɥɶɤɨ ɪɭɛɥɟɣ ɩɪɢɞɺɬɫɹ ɡɚɩɥɚɬɢɬɶ ɡɚ ɤɨɦɦɭɧɚɥɶɧɵɟ ɭɫɥɭɝɢ ɩɨɫɥɟ ɢɯ ɩɨɞɨɪɨɠɚɧɢɹ6,5%?ɧɚ
Ɉɬɜɟɬ: 
17ɋɤɨɥɶɤɨ ɜɫɟɝɨ ɨɫɟɣ ɫɢɦɦɟɬɪɢɢ,ɢɦɟɟɬ ɮɢɝɭɪɚ ɢɡɨɛɪɚɠɺɧɧɚɹ ɧɚ ɪɢɫɭɧɤɟ?
Ɉɬɜɟɬ: 
Ɇɚɬɟɦɚɬɢɤɚ. 9 ɤɥɚɫɫ. ȼɚɪɢɚɧɬ 1 |
|
|
|
8 |
|
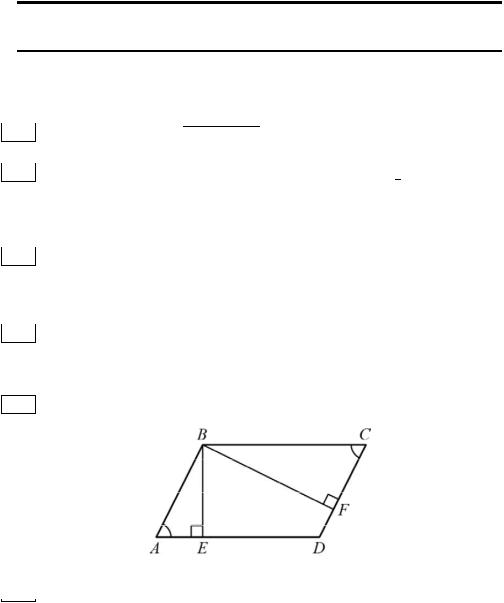
18 |
ɇɚ ɞɢɚɝɪɚɦɦɟ ɩɨɤɚɡɚɧɚ |
ɫɪɟɞɧɟɦɟɫɹɱɧɚɹ |
ɬɟɦɩɟɪɚɬɭɪɚ ɜɨɡɞɭɯɚ ɜ ɝ. ȿɤɚɬɟ- |
||
( |
ɪɢɧɛɭɪɝɟ ɋɜɟɪɞɥɨɜɫɤɟ) |
ɡɚ ɤɚɠɞɵɣ1973ɦɟɫɹɰ |
ɝɨɞɚ. |
ɉɨ ɝɨɪɢɡɨɧɬɚɥɢ |
|
|
ɭɤɚɡɵɜɚɸɬɫɹ ɦɟɫɹɰɵ, ɩɨ ɜɟɪɬɢɤɚɥɢ — |
ɬɟɦɩɟɪɚɬɭɪɚ ɜ ɝɪɚɞɭɫɚɯ ɐɟɥɶɫɢɹ. |
|||
|
ȼɵɩɢɲɢɬɟ ɧɨɦɟɪɚ ɦɟɫɹɰɟɜ, ɫɪɟɞɧɟɦɟɫɹɱɧɚɹ ɬɟɦɩɟɪɚɬɭɪɚ ɤɨɬɨɪɵɯ ɛɵɥɚ ɜɵɲɟ |
||||
|
15 ° . |
|
|
|
|
Ɉɬɜɟɬ: 














































































































19ɂɡ 900 ɧɨɜɵɯ ɮɥɟɲ-ɤɚɪɬ ɜ ɫɪɟɞɧɟɦ 54 ɧɟ ɩɪɢɝɨɞɧɵ ɞɥɹ ɡɚɩɢɫɢ. Ʉɚɤɨɜɚ ɜɟɪɨɹɬɧɨɫɬɶ ɬɨɝɨ, ɱɬɨ ɫɥɭɱɚɣɧɨ ɜɵɛɪɚɧɧɚɹ ɮɥɟɲ-ɤɚɪɬɚ ɩɪɢɝɨɞɧɚ ɞɥɹ ɡɚɩɢɫɢ?
Ɉɬɜɟɬ: 
20 |
20Ɂɚ |
ɦɢɧ ɜɟɥɨɫɢɩɟɞɢɫɬ ɩɪɨɟɯɚɥ 7 ɤɦ. ɋɤɨɥɶɤɨ ɤɢɥɨɦɟɬɪɨɜ ɨɧ ɩɪɨɟɞɟɬ ɡɚ t ɦɢɧ, |
|
|
ɟɫɥɢ ɛɭɞɟɬ ɟɯɚɬɶ? ɫ ɬɨɣ ɠɟ ɫɤɨɪɨɫɬɶɸ Ɂɚɩɢɲɢɬɟ ɫɨɨɬɜɟɬɫɬɜɭɸɳɟɟ. |
ɜɵɪɚɠɟɧɢɟ |
|
Ɉɬɜɟɬ: 
© ɆɂɈɈ 2012 ɝ. |
© ɆɂɈɈ 2012 ɝ. |
Математикакласс. 9 |
. Вариант 1 |
9 |
Часть 2
При выполнении заданий 21–26 используйте отдельный лист. Сначала укажите номер задания, а затем запишите его решение и ответ. Пишите чётко и разборчиво.
Модуль «Алгебра»
21 |
Упростите выражение: |
|
|
∙ |
|
||
|
|
|
|
22 |
Известно, что парабола проходит через точку −1; − 41 и |
её вершина |
|
|
находится в начале координат. Найдите уравнение этой параболы и вычислите, в |
||
|
каких точках она пересекает прямую = −16 |
|
|
23 |
Найдите наименьшее значение выражения и 5 − 4 + 3 + 3 − − 1 |
||
|
и значения x и y , при которых оно достигается |
|
|
|
|
Модуль «Геометрия». |
|
24 |
Окружность проходит через вершины A и C треугольника ABC и пересекает его |
||
|
стороны AB и BC в точках K и E соответственно. Отрезки AE и CK |
||
те |
перпендикулярны |
|
|
25 |
В параллелограмме ABCD проведены высоты BE и BF Докажите, |
что ABE |
|
|
подобен CBF |
|
|
 26
26  Диагонали четырёхугольника ABCD, вершины которого расположены на
Диагонали четырёхугольника ABCD, вершины которого расположены на
окружности, пересекаются в точке M. Известно, что ABC = 72°, = 102°,!" = 110° Найдите ACD
© МИОО 2012 г.

Тренировочная работа1 №
по МАТЕМАТИКЕ
4 декабря 2012 года
9 класс
Вариант 2
Район Город (населённый пункт) Школа Класс Фамилия Имя Отчество
Математика2. 9 классВариант. |
2 |
Инструкция по выполнению работы
Общее время экзамена 4 часа (240 минут)
Всего в работе 26 заданий, из которых 20 заданий базового уровня (часть I) 6и
заданий повышенногоуровня (часть II) |
|
|
|
|
||
Работа состоит:из« трёхГемо»,дулейметрия« |
Алгебра |
Реальная», « |
математика». |
|||
Модуль» |
«Алгебра содержит 11 заданий: в части I — 8 |
заданий с кратким ответом, |
||||
выбором ответа и установлением соответствия; в |
части |
II — 3 |
задания с |
полным |
||
решением |
|
|
|
|
|
|
Модуль «Геометрия» содержит 8 заданий: в части I — 5 |
заданий с кратким ответом, |
|||||
в части II — 3 задания с полным решением |
|
|
|
|
||
Модуль «Реальная математика» |
содержит 7 заданий: все задания — в части I, с |
|||||
кратким ответом и выбором ответа |
|
|
|
|
|
|
Сначала |
выполняйте задания части I. Начать |
советуем с, того модуля |
задания |
|||
которого вызывают у Вас меньше затруднений, затем переходите к другим модулям Для экономии времени пропускайте задание, которое не удаётся выполнить, сразу и переходите к следующему Если у Вас останется время, Вы сможете вернуться к пропущенным заданиям
Все необходимые вычисления, преобразования и. т. д выполняйте в черновике. Если задание содержит рисунок, то на нём можно выполнять необходимые Вам построения. Обращаем Ваше внимание на то, что записи в черновике не будут учитываться при оценивании работы Рекомендуем внимательно читать условие и проводить проверку полученногоответа
При выполнении заданий с выбором ответа обведите номер выбранного ответа в экзаменационной работе. Если Вы обвели не, тот номер то зачеркните обведённый номер крестиком и затем обведите номер правильного ответа
Если варианты ответа к заданию, не приводятся полученный ответ записывается в отведённом для этого месте. В случае записи неверного ответа зачеркните его и запишите рядом новый. Наименования указывать не надо. Если в ответе надо записать несколько чиселпишите, их через точку с запятойнапример, : –1;7
Если в задании требуется установить соответствие между некоторыми объектами, впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру
Решения заданий части II и ответы к ним записываются на отдельном. |
листе |
Текст |
|
задания можно не переписыватьнеобходимо, |
лишь указать его номер |
|
|
Баллы, полученные Вами за верно |
выполненные. задания, суммируются |
Для |
|
успешного прохождения итоговой аттестации необходимо набрать в сумме не менее 8 баллов, набранные по всей работе, из них не менее 3-х баллов по модулю «Алгебра», 2-х баллов по модулю «Геометрия»2и- х баллов по модулю «Реальная математика»
Желаем успеха!
© МИОО 2012 г
Ɇɚɬɟɦɚɬɢɤɚ. 9 ɤɥɚɫɫ. ȼɚɪɢɚɧɬ 2 |
Ɇɚɬɟɦɚɬɢɤɚ. 9 ɤɥɚɫɫ. ȼɚɪɢɚɧɬ 2 |
4 |
ɑ ɫɬɶ 1 |
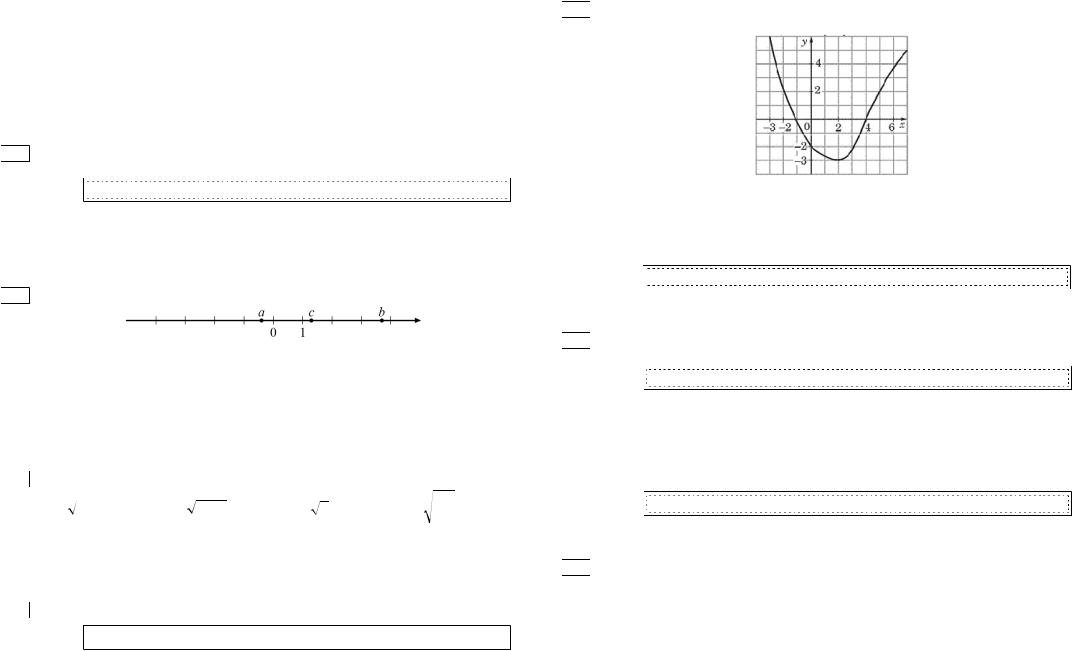
5 ɇɚ ɪɢɫɭɧɤɟ ɢɡɨɛɪɚɠɺɧ ɝɪɚɮɢɤ ɮɭɧɤɰɢɢ y f (x). Ʉɚɤɢɟ ɢɡ ɭɬɜɟɪɠɞɟɧɢɣ |
|
Ɇɨɞɭɥɶ «Ⱥɥɝɟ ɪ |
ɨɬɧɨɫɢɬɟɥɶɧɨ ɷɬɨɣ ɮɭɧɤɰɢɢ? |
ɧɟɜɟɪɧɵ ɍɤɚɠɢɬɟ ɢɯ ɧɨɦɟɪɚ. |
» |
|
|
1 ɇɚɣɞɢɬɟ: ɡɧɚɱɟɧɢɟ ɜɵɪɚɠɟɧɢɹ 6 |
1 |
2 18 |
2 |
2. |
|
|
|
|
|
|
|||
2 |
|
3 |
|
ɧɚ ɩɪɨɦɟɠɭɬɤɟ[ 1; 4] ɮɭɧɤɰɢɹ ɭɛɵɜɚɟɬ |
||
Ɉɬɜɟɬ: |
|
|
1) |
|||
|
|
|
|
2) |
f (x) |
2 ɩɪɢ 2 x 5 |
|
|
|
|
3) |
f (2) |
3 |
|
|
|
|
4) |
ɧɭɥɢ ɮɭɧɤɰɢɢ – ɱɢɫɥɚ: –1; –2; 4 |
|
2 ɇɚ ɤɨɨɪɞɢɧɚɬɧɨɣ ɩɪɹɦɨɣ ɨɬɦɟɱɟɧɵ, , |
ɱɢɫɥɚ. |
|
|
|
|
|
Ɉɬɜɟɬ: |
|
|
|
|
|
|
|||||||||
a b c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Ʉɚɤɨɟ ɢɡ ɫɥɟɞɭɸɳɢɯ ɭɬɜɟɪɠɞɟɧɢɣ ɧɟɜɟ?ɪɧɨ |
|
6 |
Ɉɥɶɝɚ 2,5ɜ |
ɪɚɡɚ ɫɬɚɪɲɟ Ɇɚɪɢɢ, ɚ Ɇɚɪɢɹ5ɧɚ |
ɥɟɬ ɫɬɚɪɲɟ. |
ɧɧɵ ȼɫɟɦ ɬɪɨɢɦ |
|||||||||||||||
|
|
|
|
|
ɜɦɟɫɬɟ 31 |
ɝɨɞ. ɋɤɨɥɶɤɨ ɥɟɬ Ɇɚɪɢɢ? |
|
|
|
|
|
|||||||||||
|
1) a c b |
2) |
b |
|
1 |
|
3) ac |
b |
4) c b a |
Ɉɬɜɟɬ: |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
ɉɪɟɞɫɬɚɜɶɬɟ ɜ ɜɢɞɟ ɞɪɨɛɢ ɜɵɪɚɠɟ ɢɟ |
10X |
5X ɢ ɚɣɞɢɬɟ ɟɝɨ ɡ ɚɱɟ ɢɟ ɩɪɢ |
||||||||
|
Ʉɚɤɨɟ ɢɡ ɞɚɧɧɵɯ ɱɢɫɟɥ ɹɜɥɹɟɬɫɹ ɢɪɪɚɰɢɨɧɚɥɶɧɵɦ? |
2X 3 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
3 |
|
|
|
X 0,5. ȼ ɨɬɜɟɬ ɡɚɩɢɲɢɬɟ ɩɨɥɭɱɟ. ɨɟ ɱɢɫɥɨ |
|
|
|
|
||||||||||||||
|
1) 0, 16 |
2) |
|
2500 |
|
3) ( |
3 )5 |
4) 5 |
4 |
|
Ɉɬɜ ɬ: |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 Ɋɟɲɢɬɟ ɧɟɪɚɜɟɧɫɬɜɨ 20 3(x 5) 19 x7 . |
|
|
|
|
|||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1) ( 4; f) |
2) |
f; |
1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
4 |
ɇɚɣɞɢɬɟ ɤɨɪɧɢ ɭɪɚɜɧɟɧɢɹ. |
16x |
2 |
0 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|||||
|
|
|
|
|
|
3) |
1 |
; f |
4) (f; 4) |
|
||||||||||||
|
Ɉɬɜɟɬ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
© ɆɂɈɈ 2012 ɝ. |
© ɆɂɈɈ 2012 ɝ. |
Ɇɚɬɟɦɚɬɢɤɚ 9 ɤɥɚɫɫ ȼɚɪɢɚɧɬ 2 |
5 |
Ɇɚɬɟɦɚɬɢɤɚ 9 ɤɥɚɫɫ ȼɚɪɢɚɧɬ 2 |
|
6 |
Ɇɨɞɭɥɶ «Ƚɟɨɦɟɬɪɢɹ» |
|
12 ɍɝɥɵ, ɨɬɦɟɱɟɧɧɵɟ ɧɚ ɪɢɫɭɧɤɟ ɨɞɧɨɣ, |
ɞɭɝɨɣ. |
ɪɚɜɧɵ ɇɚɣɞɢɬɟ ɭɝɨɥ . Ɉɬɜɟɬ ɞɚɣɬɟ |
|
|
ɜ ɝɪɚɞɭɫɚɯ. |
|
|
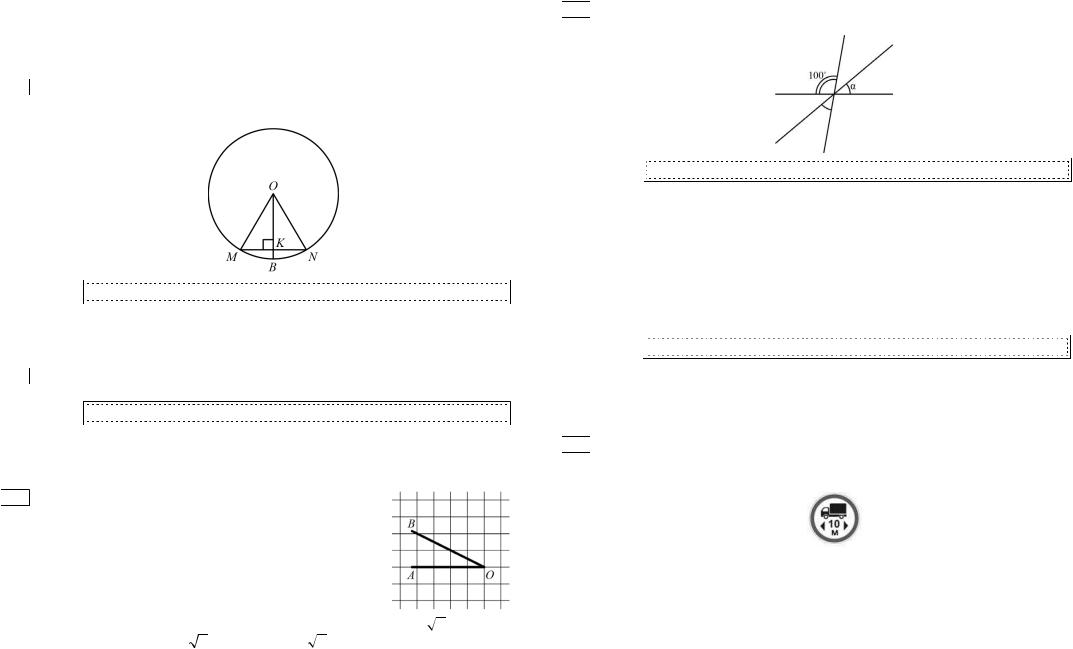
9Ɋɚɞɢɭɫ OB ɨɤɪɭɠɧɨɫɬɢ ɫ ɰɟɧɬɪɨɦ ɜ ɬɨɱɤɟ O ɩɟɪɟɫɟɤɚɟɬ ɯɨɪɞɭ MN ɜ ɟɺ
|
ɫɟɪɟɞɢɧɟ – ɬɨɱɤɟ |
K. ɇɚɣɞɢɬɟ ɞɥɢɧɭ, ɯɨɪɞɵ |
|
MN ɟɫɥɢ |
KB |
1ɫɦ, |
ɚ ɪɚɞɢɭɫ |
|
|
|
|
|
||||||||
|
ɨɤɪɭɠɧɨɫɬɢ13ɪɚɜɟɧ |
ɫɦ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɉɬɜɟɬ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
ɍɤɚɠɢɬɟ ɜ ɨɬɜɟɬɟ ɧɨɦɟɪɚ. |
ɜɟɪɧɵɯ ɭɬɜɟɪɠɞɟɧɢɣ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) |
ȿɫɥɢ ɩɪɢ ɩɟɪɟɫɟɱɟɧɢɢ ɞɜɭɯ ɩɪɹɦɵɯ ɬɪɟɬɶɟɣ ɫɭɦɦɚ ɧɚɤɪɟɫɬ ɥɟɠɚɳɢɯ ɭɝɥɨɜ |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
,ɪɚɜɧɚ180q. ɬɨ ɩɪɹɦɵɟ ɩɚɪɚɥɥɟɥɶɧɵ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
ȿɫɥɢ ɜ ɩɪɹɦɨɭɝɨɥɶɧɢɤɟ ɞɢɚɝɨɧɚɥɢ ɩɟɪɩɟɧɞɢɤɭɥɹɪɧɵ, ɬɨ -ɷɬɨɬ |
ɩɪɹɦɨ |
||
|
Ɉɬɜɟɬ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
ɭɝɨɥɶɧɢɤ – ɤɜɚɞɪɚɬ. |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
3) |
ȿɫɥɢ ɞɜɚ ɭɝɥɚ ɢ ɫɬɨɪɨɧɚ ɨɞɧɨɝɨ ɬɪɟɭɝɨɥɶɧɢɤɚ ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ ɪɚɜɧɵ ɞɜɭɦ |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɭɝɥɚɦ ɢ ɫɬɨɪɨɧɟ ɞɪɭɝɨɝɨ ɬɪɟɭɝɨɥɶɧɢɤɚ, ɬɨ ɬɚɤɢɟ ɬɪɟɭɝɨɥɶɧɢɤɢ. ɪɚɜɧɵ |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɉɬɜɟɬ: |
|
|
|
|
10 |
Ⱦɢɚɝɨɧɚɥɶ ɬɪɚɩɟɰɢɢ ɞɟɥɢɬ ɟɺ ɫɪɟɞɧɸɸ ɥɢɧɢɸ, |
ɧɚ ɨɬɪɟɡɤɢ4 |
ɪɚɜɧɵɟ |
ɫɦ ɢ 3 ɫɦ. |
|
|
|
|
|
|||||||||||
|
ɇɚɣɞɢɬɟ ɦɟɧɶɲɟɟ ɨɫɧɨɜɚɧɢɟ ɬɪɚɩɟɰɢɢ. |
|
|
|
|
|
|
|
|
|
|
Ɇɨɞɭɥɶ «Ɋɟ ɥɶɧ ɹ ɦ ɬɟɦ ɬɢɤ » |
|
|
||||||
|
Ɉɬɜɟɬ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
Ⱦɨɪɨɠɧɵɣ ɡɧɚɤ, ɢɡɨɛɪɚɠɺɧɧɵɣɈɝɪɚɧɢɱɟɧɢɟɧɚ«ɪɢɫɭɧɤɟ, ɧɚɡɵɜɚɟɬɫɹ |
|
ɞɥɢɧɵ». |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ȿɝɨ ɭɫɬɚɧɚɜɥɢɜɚɸɬ ɬɚɦ, ɝɞɟ ɡɚɩɪɟɳɺɧ ɩɪɨɟɡɞ ɬɪɚɧɫɩɨɪɬɧɨɝɨ ɫɪɟɞɫɬɜɚ, ɝɚɛɚɪɢɬɵ |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
ɤɨɬɨɪɨɝɨ ɫ ɝɪɭɡɨɦ ɢɥɢ) ɛɟɡ ɝɪɭɡɚ ɩɪɟɜɵɲɚɸɬ ɭɫɬɚɧɨɜɥɟɧɧɭɸ. |
ɞɥɢɧɭ |
|
||
11 |
ɑɟɦɭ ɪɚɜɟɧ ɫɢɧɭɫ ɭɝɥɚ AOB? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ʉɚɤɨɦɭ ɢɡ ɞɚɧɧɵɯ ɬɪɚɧɫɩɨɪɬɧɵɯ ɫɪɟɞɫɬɜ ɷɬɨɬ ɡɧɚɤ ɡɚɩɪɟɳɚɟɬ ɩɪɨɟɡɞ? |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) |
ɛɟɧɡɨɜɨɡɭ ɞɥɢɧɨɣ 7600 ɦɦ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
ɚɜɬɨɦɨɛɢɥɸ Ƚɚɡɟɥɶ ɞɥɢɧɨɣ 6330 ɦɦ |
|
|
|
|
1) |
1 |
|
2) |
2 |
|
3) |
|
1 |
|
4) |
5 |
|
3) |
ɚɜɬɨɬɨɩɥɢɜɨɡɚɩɪɚɜɳɢɤɭ ɞɥɢɧɨɣɦɦ 10200 |
|
|
|||
|
|
|
|
|
|
|
ɚɜɬɨɰɢɫɬɟɪɧɟ ɞɥɢɧɨɣ 8250 ɦɦ |
|
|
|||||||||||
|
2 |
|
5 |
|
|
|
5 |
|
|
|
|
4) |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||
© ɆɂɈɈ 2012 ɝ |
© ɆɂɈɈ 2012 ɝ |
Ɇɚɬɟɦɚɬɢɤɚ 9 ɤɥɚɫɫ ȼɚɪɢɚɧɬ 2 |
7 |
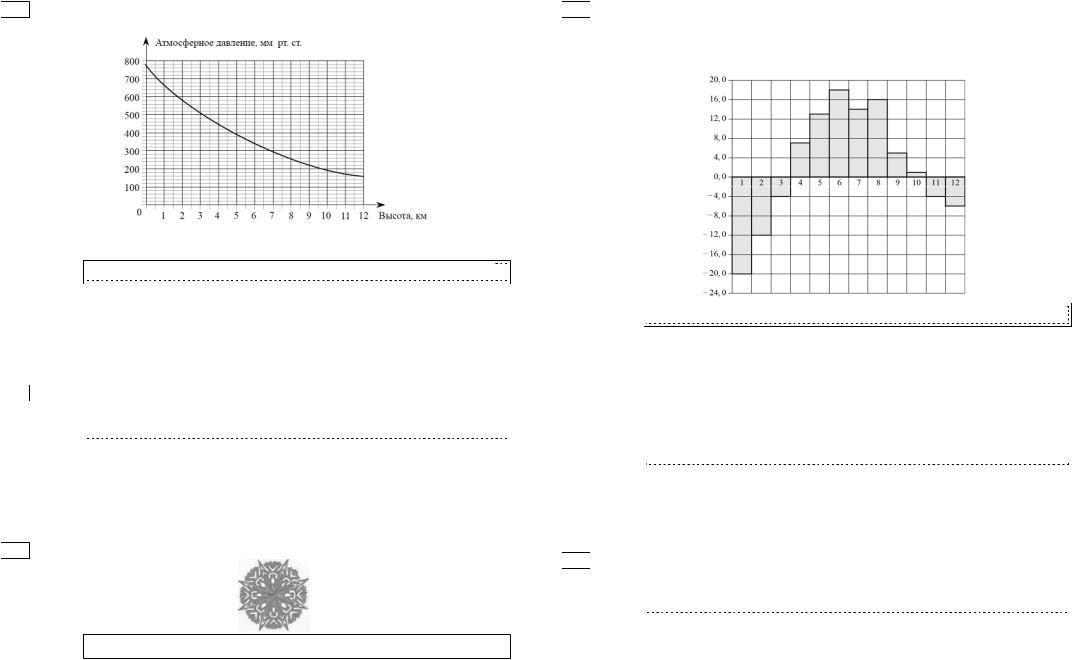
15ɇɚ ɝɪɚɮɢɤɟ ɢɡɨɛɪɚɠɟɧɚ ɡɚɜɢɫɢɦɨɫɬɶ ɚɬɦɨɫɮɟɪɧɨɝɨ( ɞɚɜɥɟɧɢɹ ɜ ɦɢɥɥɢɦɟɬɪɚɯ ɪɬɭɬɧɨɝɨ ɫɬɨɥɛɚ) ɨɬ ɜɵɫɨɬɵ ɧɚɞ ɭɪɨɜɧɟɦ ɦɨɪɹ (ɜ ɤɢɥɨɦɟɬɪɚɯ).
ɇɚ ɫɤɨɥɶɤɨ ɦɢɥɥɢɦɟɬɪɨɜ ɪɬɭɬɧɨɝɨ ɫɬɨɥɛɚ ɨɬɥɢɱɚɟɬɫɹ ɞɚɜɥɟɧɢɟ2 ɧɚ ɜɵɫɨɬɟ ɤɦ |
|
ɨɬ ɞɚɜɥɟɧɢɹ8 |
ɧɚ ɜɵɫɨɬɟ ɤɦ? |
Ɉɬɜɟɬ: 











































































































16 |
ɉɥɚɬɚ ɡɚ ɤɨɦɦɭɧɚɥɶɧɵɟ800ɭɫɥɭɝɢ ɫɨɫɬɚɜɥɹɥɚ |
. ɪ ɋɤɨɥɶɤɨ ɪɭɛɥɟɣ ɩɪɢɞɺɬɫɹ |
|
ɡɚɩɥɚɬɢɬɶ ɡɚ ɤɨɦɦɭɧɚɥɶɧɵɟ ɭɫɥɭɝɢ ɩɨɫɥɟ ɢɯ ɩɨɞɨɪɨɠɚɧɢɹ5,5%?ɧɚ |
|
Ɉɬɜɟɬ: 
ɜɫɟɝɨ |
ɋɤɨɥɶɤɨ |
ɨɫɟɣ ɫɢɦɦɟɬɪɢɢ ɢɦɟɟɬ ɮɢɝɭɪɚ ɢɡɨɛɪɚɠɺɧɧɚɹ ɧɚ ɪɢɫɭɧɤɟ |
? |
17 |
|
, |
Ɉɬɜɟɬ: 











































































































Ɇɚɬɟɦɚɬɢɤɚ 9 ɤɥɚɫɫ ȼɚɪɢɚɧɬ 2 |
|
|
|
|
|
|
8 |
|
18 |
ɇɚ ɞɢɚɝɪɚɦɦɟ |
ɩɨɤɚɡɚɧɚ |
ɫɪɟɞɧɟɦɟɫɹɱɧɚɹ |
ɬɟɦɩɟɪɚɬɭɪɚ |
ɜɨɡɞɭɯɚ |
ɜ ɝ. ȿɤɚɬɟ- |
||
ɟɪɞɥɨɜɫɤɟ( ɪɢɧɛɭɪɝɟ |
) |
ɡɚ ɤɚɠɞɵɣ1973ɦɟɫɹɰ |
. |
ɝɨɞɚ ɉɨ ɝɨɪɢɡɨɧɬɚɥɢ |
||||
|
ɭɤɚɡɵɜɚɸɬɫɹ ɦɟɫɹɰɵ, ɩɨ |
ɜɟɪɬɢɤɚɥɢ — |
ɬɟɦɩɟɪɚɬɭɪɚ ɜ |
ɝɪɚɞɭɫɚɯ. |
ɟɥɶɫɢɹ |
|||
ɋ |
ȼɵɩɢɲɢɬɟ ɧɨɦɟɪɚ ɦɟɫɹɰɟɜ, ɫɪɟɞɧɟɦɟɫɹɱɧɚɹ ɬɟɦɩɟɪɚɬɭɪɚ |
ɤɨɬɨɪɵɯ ɛɵɥɚ ɧɢɠɟ |
||||||
–10 ° . |
|
|
|
|
|
|
|
|
Ɉɬɜɟɬ: 














































































































19ɂɡ 1400 ɧɨɜɵɯ ɤɚɪɬ ɩɚɦɹɬɢ ɜ ɫɪɟɞɧɟɦ 56 ɧɟɢɫɩɪɚɜɧɵ. Ʉɚɤɨɜɚ ɜɟɪɨɹɬɧɨɫɬɶ ɬɨɝɨ, ɱɬɨ ɫɥɭɱɚɣɧɨ ɜɵɛɪɚɧɧɚɹ ɤɚɪɬɚ? ɩɚɦɹɬɢ ɢɫɩɪɚɜɧɚ
Ɉɬɜɟɬ: 
20Ɇɨɬɨɰɢɤɥɢɫɬ ɩɪɨɟɯɚɥ 23 ɤɦ ɡɚ 15 ɦɢɧ. ɋɤɨɥɶɤɨ ɤɢɥɨɦɟɬɪɨɜ ɨɧ ɩɪɨɟɞɟɬ ɡɚ t ɦɢɧ, ɟɫɥɢ ɛɭɞɟɬ ɟɯɚɬɶ? ɫ ɬɨɣ ɠɟ ɫɤɨɪɨɫɬɶɸ Ɂɚɩɢɲɢɬɟ ɫɨɨɬɜɟɬɫɬɜɭɸɳɟɟ. ɜɵɪɚɠɟɧɢɟ
Ɉɬɜ ɬ: 
© ɆɂɈɈ 2012 ɝ |
© ɆɂɈɈ 2012 ɝ |

Ɇɚɬɟɦɚɬɢɤɚ 9 ɤɥɚɫɫ ȼɚɪɢɚɧɬ 2 |
9 |
2ɑ ɫɬɶ
ɉɪɢ ɜɵɩɨɥɧɟɧɢɢ ɡɚɞɚɧɢɣ 21–26 ɢɫɩɨɥɶɡɭɣɬɟ ɨɬɞɟɥɶɧɵɣ ɥɢɫɬ. ɋɧɚɱɚɥɚ ɭɤɚɠɢɬɟ ɧɨɦɟɪ ɡɚɞɚɧɢɹ, ɚ ɡɚɬɟɦ ɡɚɩɢɲɢɬɟ ɟɝɨ ɪɟɲɟɧɢɟ ɢ ɨɬɜɟɬ. ɉɢɲɢɬɟ ɱɺɬɤɨ ɢ ɪɚɡɛɨɪɱɢɜɨ.
Ɇɨɞɭɥɶ «Ⱥɥɝɟ ɪ »
|
|
|
10 2n |
|
|
|
|
21 |
ɍɩɪɨɫɬɢɬɟ: |
ɜɵɪɚɠɟɧɢɟ. |
2n 1 2n 1 |
|
|
|
|
22 |
ɂɡɜɟɫɬɧɨ, ɱɬɨ ɩɚɪɚɛɨɥɚ ɩɪɨɯɨɞɢɬ ɱɟɪɟɡ ɬɨɱɤɭ B1; |
1 |
ɢ ɟɺ ɜɟɪɲɢɧɚ ɧɚɯɨɞɢɬɫɹ |
||||
4 |
|||||||
|
|
|
|
|
|
||
|
ɜ ɧɚɱɚɥɟ ɤɨɨɪɞɢɧɚɬ. ɇɚɣɞɢɬɟ ɭɪɚɜɧɟɧɢɟ ɷɬɨɣ ɩɚɪɚɛɨɥɵ ɢ ɜɵɱɢɫɥɢɬɟ, ɜ ɤɚɤɢɯ |
||||||
|
ɬɨɱɤɚɯ ɨɧɚ ɩɟɪɟɫɟɤɚɟɬ. ɩɪɹɦɭɸ y |
9 |
4y 6)2 (3x 4y 2)2 ɢ |
||||
23 |
ɇɚɣɞɢɬɟ |
ɧɚɢɦɟɧɶɲɟɟ |
ɡɧɚɱɟɧɢɟ |
ɜɵɪɚɠɟɧɢɹ x (5 |
|||
ɡɧɚɱɟɧɢɹ x ɢ y, ɩɪɢ ɤɨɬɨɪɵɯ ɨɧɨ ɞɨɫɬɢɝɚɟɬɫɹ.
Ɇɨɞɭɥɶ «Ƚɟɨɦɟɬɪɢɹ»
24Ɉɤɪɭɠɧɨɫɬɶ ɩɪɨɯɨɞɢɬ ɱɟɪɟɡ ɜɟɪɲɢɧɵ A ɢ C ɬɪɟɭɝɨɥɶɧɢɤɚ ABC ɢ ɩɟɪɟɫɟɤɚɟɬ ɟɝɨ ɫɬɨɪɨɧɵ AB ɢ BC ɜ ɬɨɱɤɚɯ K ɢ E ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ. Ɉɬɪɟɡɤɢ AE ɢ CK ɩɟɪɩɟɧɞɢɤ. ɭɥɹɪɧɵ, ɇɚɣɞɢɬɟ ABC ɟɫɥɢ KCB 20 .
25ȼ ɨɫɬɪɨɭɝɨɥɶɧɨɦ ɬɪɟɭɝɨɥɶɧɢɤɟ ABC ɩɪɨɜɟɞɟɧɵ ɜɵɫɨɬɵ CE, ɢ AD. Ⱦɨɤɚɠɢɬɟ ɱɬɨ ǻABD ɩɨɞɨɛɟɧ ǻCBE.
26 Ⱦɢɚɝɨɧɚɥɢ ɱɟɬɵɪɺɯɭɝɨɥɶɧɢɤɚ ABCD, ɜɟɪɲɢɧɵ ɤɨɬɨɪɨɝɨ ɪɚɫɩɨɥɨɠɟɧɵ ɧɚ ɨɤɪɭɠɧɨɫɬɢ ɩɟɪɟɫɟɤɚɸɬɫɹ ɜ ɬɨɱɤɟ M. ɂɡɜɟɫɬɧɨ, ɱɬɨ ABC 74 , BCD 102 ,
AMD 112 . ɇɚɣɞɢɬɟ ACD
© ɆɂɈɈ 2012 ɝ
