3. Описание установки

В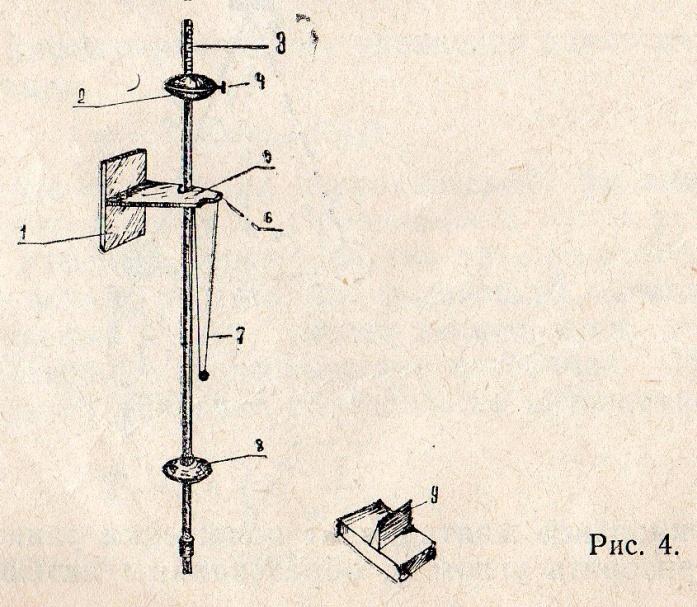данной лабораторной работе законы колебательного движения будем изучать с помощью универсального маятника (прибор ФП1А).

Прибор ФП1А (рис. 4) включает в себя настенный кронштейн 1, на котором смонтирована подушка опорных призм 5 и узел 6 крепления нитей бифилярного подвеса математического маятника 7. На кронштейне 1 подвешен (на опорной призме 5) физический маятник, представляющий собой металлический стержень 3, на котором закреплены два тяжелых груза — чечевицы 2 и 8. Таким образом, универсальный маятник (прибор ФП1А) сочетает в себе два типа маятников: физический и математи­ческий. Конструкция прибора обеспечивает вращение обоих маятников около одной и той же оси, проходящей через опорную плоскость подушек 5.

В комплект прибора входит специальная подставка 9 с призмой для нахождения центра масс маятника.

4. Порядок выполнения работы

Задание 1. Определение момента инерции физического маятника.

Приборы и принадлежности: физический маятник (прибор ФП1А), секундомер, металлическая линейка с ценой деления 1 мм, подставка с призмой для нахождения центра тяжести маятника.

При выполнении задания № 1 рекомендуется соблюдать указанную ниже последовательность выполнения работы.

1. Вывести и записать, используя выражение (15), расчётную формулу для определения момента инерции физического маятника.

2. Приготовить таблицу для записи исходных данных и результатов опыта (табл. 1).

Номер опыта	m, кг	∆m, кг	L, м	∆L, м	N	τ, с	Т, с	∆Т, с	I, кг·м2	∆I, кг·м2
1 . . . n

3. Зафиксировать грузы (чечевицы) на стержне физического маятника по указанию преподавателя.

Определить и записать в табл. 1 массу т физического маят­ника (масса обычно указана на маятнике или сообщается преподавателем).

4. Положить маятник на ребро трёхгранной призмы (рис.5) и, добившись положения устойчивого равновесия маятника, измерить длину L от точки подвеса до центра масс этого маятни­ка. Указанные измерения величины L выполнить не менее 5-ти раз. Результаты всех измерений записать в табл. 1.

5. Повесить маятник на кронштейн 1 (рис.4). Отклонить маятник на угол 5—10° и предоставить ему возможность совершать малые колебания.

6. Измерить с помощью секундомера время 20-ти полных колебаний. Измеренияповторить не менее 5-ти раз. Число полных колебанийN может быть и другим (N = 30, N=40 и т. д.). Результаты всех измерений записать в табл. 1.

Обработка результатов измерений

1. Записать с точностью до второго знака значения ускорения силы тяжести и числа и определить их предельные погрешности.

2. Вычислить , а также абсолютные погрешности.

3. Определить, используя расчётную формулу, наиболее вероятное значение момента инерции .

4. Вычислить среднее значение абсолютной погрешности:

где — относительная погрешность, вычисляемая по формуле:

.

Записать результаты расчётов в виде:

_..

6. Определить доверительную вероятность для доверительного интервала:

.

7. Записать окончательный результат в следующем виде:

.

8. Вычислить по теореме Штейнера (17) (используя результаты измерений и расчётов) момент инерции рассматриваемого маятника относительно оси, проходящей через центр масс этого маятника и параллельной оси, относительно которой данный маятник совершает колебания (рис.4).

Задание 2. Исследование зависимости периода колебаний математического маятника от его длины.

Приборы и принадлежности: математический маятник, секундомер, линейка металлическая с ценой деления 1 мм, угольник.

При выполнении задания рекомендуется соблюдать следующую последовательность.

1. Ознакомиться с лабораторной установкой и проверить (в присутствии лаборанта) её работу.

2. Составить таблицу результатов опытов по прилагаемой форме (табл. 2).

Номер опыта	Длина маятника l, м	Число колебаний N	Продолжительность колебаний маятника в данном опыте				Период колебаний Т, с
			τ1 , с	τ2 , с	τ3 , с	τср , с
1
…

3. Установить длину маятника не менее 50 см и измерить её.

4. Отклонить маятник от положения равновесия на угол 5-10° и предоставить ему свободно колебаться.

5. Замерить с помощью секундомера время 20-ти полных колебаний. Измеренияповторить три раза.

6. Повторить аналогичные опыты ещё 3-4 раза, каждый раз увеличивая длину маятника на 15—20 см.

7. Записать в табл. 2 исходные данные и результаты наблюдения (длину маятника , число колебаний, продолжительность колебаний) для каждогоi-гo опыта.

8. Вычислить для каждого опыта период колебания математического маятника .

9. Построить на миллиметровой бумаге в прямоугольной системе координат теоретический график зависимости периода колебаний математического маятника от его длины, используя формулу (18).

10. Нанести на график теоретической зависимости экспериментальные точки с координатами из табл. 2 и соединить их плавной линией.

11. Оценить соответствие (расхождение) опытных данных с теоретической зависимостью и объяснить причины возможного расхождения результатов эксперимента и теоретической кривой.