
Министерство образования и науки
РОССИЙСКОЙ ФЕДЕРАЦИИ
ОРЛОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ
ЭКОНОМИКИ И ТОРГОВЛИ
С.В.Дёминова


Студента (ки) группы____________
ФИО______________________________
ОРЕЛ - 2012
Тема 1: Парная регрессия и корреляция
Задача 1.
Фирма провела рекламную кампанию. Через 10 недель фирма решила проанализировать эффективность этого вида рекламы, сопоставив недельные объёмы продаж с расходами на рекламу:
|
Номер региона |
Недельные объёмы продаж, тыс. руб. |
Расходы на рекламу, тыс. руб. |
|
1 |
72 |
5 |
|
2 |
76 |
8 |
|
3 |
78 |
6 |
|
4 |
70 |
5 |
|
5 |
68 |
3 |
|
6 |
80 |
9 |
|
7 |
82 |
12 |
|
8 |
65 |
4 |
|
9 |
62 |
3 |
|
10 |
90 |
10 |
Задание:
1. Постройте линейное уравнение парной регрессии уотх.
2. Рассчитайте линейный коэффициент парной корреляции
3. Рассчитайте коэффициент детерминации.
4. Определите среднюю ошибку аппроксимации.
5. Оцените статистическую значимость параметров регрессии и корреляции.
6. С вероятностью 0,95 оцените доверительный интервал ожидаемой величины недельного объёма продаж компании с уровнем расходов на рекламу в 13 тыс. руб.
Решение:
1.Для расчета параметров уравнения линейной регрессии строим расчетную таблицу:
|
№п/п |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
Итого |
|
|
|
|
|
|
|
|
|
|
Рассчитаем промежуточные показатели:
![]()
![]()
![]()
![]()
Рассчитаем параметры уравнения:

Получено следующее уравнение регрессии:
![]()
Коэффициент регрессии
![]() показывает, что
показывает, что
2. Тесноту линейной связи оценивает коэффициент корреляции. Для его определения рассчитаем следующие показатели:
Дисперсию факторного признака
![]() :
:
![]()
Среднее квадратическое отклонение
факторного признака
![]()
![]()
Дисперсию результативного признака
![]()
![]()
Среднее квадратическое отклонение результативного признака y
![]()
Далее рассчитаем коэффициент корреляции:
![]()
Так как rxy
3.Определим коэффициент детерминации:
D=![]()
Он показывает, что вариация результативного
признака
![]() на ….% зависит от вариации факторного
признака
на ….% зависит от вариации факторного
признака![]()
4.Качество модели оценим с помощью средней ошибки аппроксимации:
![]()
5.Оценку статистической значимости параметров регрессии проведем с помощьюt-критерия Стьюдента.
Определим остаточную дисперсию:
![]()
Определим случайные ошибки параметров уравнения и коэффициента корреляции:

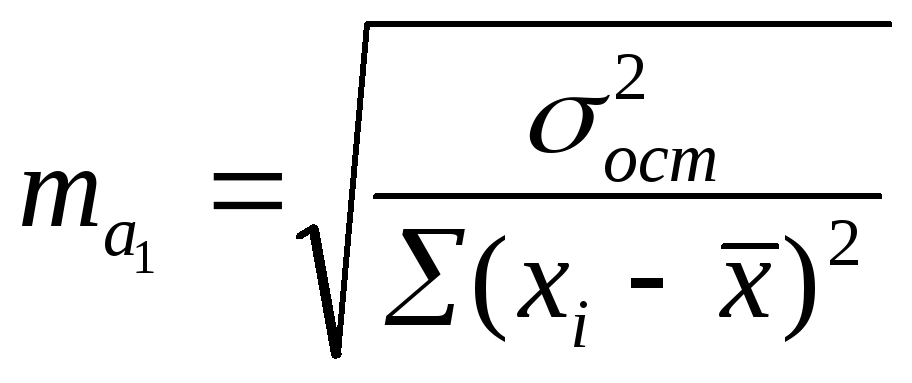
![]()
Определим расчетные значения t-критерия Стьюдента.
![]()
![]()
![]()
tтабл. при заданных степенях свободыdf=n-2 = 10 – 2 = 8 и уровне значимости 5% (уровень надёжности 0,95 (95%)) составляет 2,306.
Сравним расчетные значения t-критерия Стьюдента с табличным:
6. Полученные оценки уравнения
регрессии позволяют его использовать
для прогнозирования. Предполагаемые
расходы на рекламу на следующую
неделю составят 13 тыс. руб., то есть
![]() = 13 тыс. руб.
= 13 тыс. руб.
Тогда прогнозное значение недельных объёмов продаж составит:
![]()
Ошибка прогноза составит:
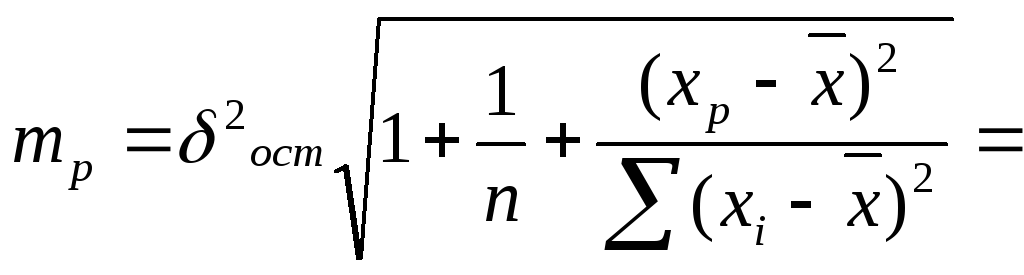
Предельная ошибка прогноза, которая в 95% не будет превышена, составит следующую величину:
![]()
Построим доверительный интервал прогноза:
![]()
![]()
Выполненный прогноз показывает, что при уровне расходов на рекламу в 13 тыс. руб., недельный объём продаж фирмы будет находиться в пределах от …….. тыс. руб. до ……………. тыс. руб.
Задача 2. При исследовании корреляционной зависимости между ценой на нефть и индексом нефтяных компаний получены следующие данные:
![]() =16,2
(ден. ед.),
=16,2
(ден. ед.),![]() =4000
(усл. ед.), (
=4000
(усл. ед.), (![]() -
-![]() *
*![]() )
= 40,
)
= 40,![]() =4,
=4,![]() =500.
=500.
Задание:
составьте уравнение регрессии;
используя полученное уравнение регрессии, найдите среднее значение индекса при цене на нефть 16,5 ден. ед.
