Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Брестский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

КР№1_задания на 2012 (осень)

.pdf

Скачиваний:

Добавлен:

01.03.2016

Размер:

354.34 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

Организационно-методические указания

В контрольную работу по разделам «Элементы линейной алгебры и аналитической геометрии», «Введение в математический анализ» и «Дифференциальное исчисление функций одной переменной» общего курса дисциплины «Математика» включено восемь заданий. В нумерации задач первое число – номер задания (задачи), второе (после точки)

– номер варианта.

Контрольная работа должна выполняться студентом в соответствии со своим вариантом. Номер варианта определяется по двум послед-

ним цифрам шифра (номера зачетной книжки студента).

При выполнении контрольной работы условия задач нужно запи-

сывать полностью. В случае, если задача имеет общую формулировку, ее условие следует переписывать, заменяя общие данные конкретными, соответствующими номеру варианта.

Решение всех задач приводить подробно и аккуратно, давать достаточные пояснения и делать необходимые рисунки и таблицы.

В конце каждой задачи должен быть ответ.

Контрольные вопросы курса «Высшая математика»

Iсеместр

1.Определители, их свойства и вычисление.

2.Решение систем линейных алгебраических уравнений по формулам Крамера.

3.Матрицы. Операции над матрицами.

4.Обратная матрица. Матричный метод решения систем линейных алгебраических уравнений.

5.Ранг матрицы. Метод Гаусса решения систем линейных алгебраических уравнений.

6.Системы линейных однородных уравнений.

7.Векторы, линейные операции над ними.

8.Линейная зависимость и независимость векторов. Базис.

9.Декартова система координат. Координаты вектора. Условие коллинеарности векторов.

10.Скалярное произведение векторов, его свойства, вычисление, приложения. Условия ортогональности векторов.

11.Векторное произведение вектора, его свойства, нахождение, приложения.

12.Смешанное произведение векторов, его вычисление, приложения. Условия компланарности векторов.

13.Радиус вектор. Полярная система координат.

14.Линейный оператор. Матрица линейного оператора.

15.Собственные значения и собственные векторы линейного оператора.

16.Прямая на плоскости.

17.Кривая второго порядка. Её характеристики.

18.Плоскость.

19.Прямая в пространстве. Взаимное расположение двух прямых.

20.Взаимное расположение прямой и плоскости.

21.Поверхности второго порядка.

22.Понятие функции одной переменной. Элементарные функции. Алгебраические функции.

23.Предел числовой последовательности. Свойства сходящихся последовательностей.

24.Число е.

25.Первый и второй замечательные пределы.

26.Бесконечно малые и бесконечно большие функции и их свойства.

27.Эквивалентные бесконечно малые функции, их приложения к нахождению пределов.

28.Непрерывность функции. Точки разрыва.

29.Свойства функций непрерывных в точке и непрерывных на отрезке.

30.Производная функции. Ее геометрический и механический смыслы.

31.Правила дифференцирования и таблица производных.

32.Производные обратной функции и неявно заданной. Логарифмическая производная.

33.Дифференциал функции, его геометрический смысл. Инвариантность формы дифференциала.

34.Производные и дифференциалы высших порядков.

35.Дифференцирование параметрически заданной функции.

36.Теорема Ферма. Теорема Ролля.

37.Теорема Коши. Теорема Лагранжа.

38.Правило Лопиталя.

39.Формула Тейлора с остаточным членом в форме Пеано и Лагранжа.

40. Разложение по формуле Тейлора функций ex , sin x , cos x , ln(1+ x), (1+ x)α .

41.Условия монотонности функции.

42.Необходимое и достаточные условия экстремума.

43.Выпуклость функции. Точки перегиба. Необходимые и достаточные условия существования точки перегиба.

44.Асимптоты графика функции.

45.Вектор-функция скалярного аргумента. Касательная и нормальная плоскость к годографу. Кривизна кривой.

Задания контрольной работы

Задание 1. В задачах 1.1.-1.30. проверьте совместность системы линейных уравнений и в случае совместности решите ее тремя способами:

1.по формулам Крамера;

2.матричным методом (с помощью обратной матрицы);

3.методом Гаусса.

2x −3y −5z =1,

1.1.3x + y −2z = −4,x −2y + z = 5.

2x − y +3z =1,

1.4.x + 2y + z = 8,4x −3y −2z = −1.x −3y + z = 2,

1.7.2x + y +3z = 3,2x − y −2z = 8.

x −2y + z = 4,

1.10.2x + y +3z = 5,3x + 4y + z = −2.

2x +3y − z = 2,

1.13.x + 2y +3z = 0,x − y −2z = 6.

2x −3y + z = 3,

1.16.x + y −2z = 4,3x −2y + 6z = 0.

x + y −2z =1,

1.19.2x +3y + z = 0,x −2y − z = 7.

x + y + 2z = −1,

1.22.2x − y + 2z = −4,4x + y + 4z = −2.

x + y − z =1,

1.25.8x +3y −6z = 2,4x + y −3z = 3.

2x +3y − z = 2,

1.2.x − y +3z = −4,

3x +5y = 4.

2x − y + 3z = 3,

1.5.x + 2y + z = 2,x −3y + 4z = −1.

4x +3y −2z = −1,

1.8.3x + y + z = 3,x −2y −3z = 8.

3x + y −2z =1,

1.11.x −2y +3z = 5,2x +3y − z = −4.

x +5y − z = −1,

1.14.2x + y −2z = 7,x − 4y + z = 0.

3x −2y + 2z = 3,

1.17.2x + y − z = −5,

5x − y +3z = 4.

x + 2y − 4z = 0,

1.20.3x + y −3z = −1,2x − y +5z = 3.

3x + 4y + 2z = −1,

1.23.2x − y −3z = −5,x +5y + z = 0.

2x − y +5z =1,

1.26.x −3y + z = −2,

2x + y − z = 3.

5x −2y + z = −1,

1.3.2x + y + 2z = 6,

x −3y − z = −5.

x −3y − z =1,

1.6.2x + y + z = −7,

2x − y −3z = 5.

3x +3y + 2z = −1,

1.9.2x + y − z = 3,x −2y −3z = 4.

3x + y + 2z = −4,

1.12.x −2y − z = −1,

2x +3y + 2z = 0.

3x + 2y − z = 3,

1.15.x − y + 2z = −4,

2x + 2y + z = 4.

2x −3y +3z = 0,

1.18.x + y −2z = −7,

x −2y +3z = 3.

x + 2y − z = 2,

1.21.2x − y −3z = −1,3x +3y + z = 3.

x − 4y −2z = −5,

1.24.3x + y + z = 5,3x −5y −6z = −8.

x + y −2z = 0,

1.27.3x − y − z =1,5x −3y + z = 5.

3x	− y + 2z	=1,	4x −3y		−2z	= 2,	3x	+ y + z = 4,
1.28. 2x	+ y +3z	= 4,	1.29. 3x	+ y − z = 2,			1.30. 2x	+3y −2z = 5,
		= 3.		+5y	+3z	= 5.
x −2y +5z		= 3.	2x	+5y	+3z	= 5.	x − 4y −2z = −3.

Задание 3. В задачах 3.1.-3.30. даны вершины треугольника АВС:

A(x1,y1), B(x2,y2), C(x3,y3). Найти:

1)длину стороны АС;

2)длину высоты ВН, проведенной из вершины В;

3)уравнение высоты ВН;

4)уравнение медианы, проведенной из вершины С;

5)сделать чертеж.

	A	B	C
3.1.	(-8;2)	(3;6)	(-3;2)
3.3.	(-7;1)	(-1;5)	(-4;1)
3.5.	(3;1)	(0;5)	(9;1)
3.7.	(-3;-4)	(3;-3)	(-6;-6)
3.9.	(-4;3)	(2;1)	(-4;8)
3.11.	(-6;2)	(5;6)	(-1;2)
3.13.	(-5;1)	(1;5)	(-2;1)
3.15.	(1;1)	(7;1)	(-2;5)
3.17.	(-1;-4)	(4;-3)	(-5;-8)
3.19.	(-6;3)	(0;1)	(-6;8)
3.21.	(-8;3)	(4;7)	(-3;3)
3.23.	(-7;2)	(-1;6)	(-4;2)
3.25.	(3;-1)	(9;-1)	(0;-3)
3.27.	(-3;0)	(3;7)	(3;1)
3.29.	(-4;4)	(2;2)	(-4;9)

	А	В	С
3.2.	(-8;-2)	(4;5)	(-3;-2)
3.4.	(-7;-1)	(3;6)	(-4;-1)
3.6.	(3;-2)	(9;-2)	(0;5)
3.8.	(-2;4)	(3;4)	(-6;-6)
3.10.	(-3;3)	(3;1)	(-3;9)
3.12.	(-6;-2)	(4;2)	(-1;-2)
3.14.	(-5;-1)	(3;5)	(-2;-1)
3.16.	(1;-1)	(7;-1)	(-2;3)
3.18.	(1;-4)	(9;-3)	(6;-3)
3.20.	(-6;2)	(2;7)	(0;0)
3.22.	(-8;-3)	(0;0)	(-3;-3)
3.24.	(-7;-2)	(0;3)	(-4;-2)
3.26.	(0;-1)	(-3;-3)	(6;-1)
3.28.	(-3;1)	(3;8)	(3;2)
3.30.	(-4;2)	(2;0)	(-4;7)

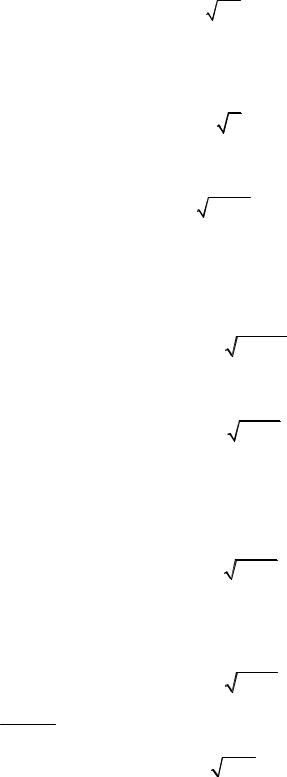
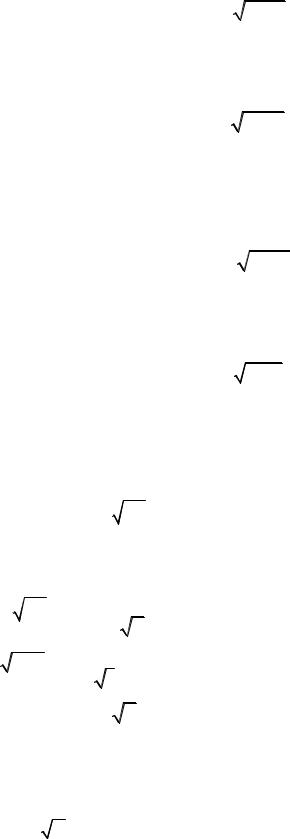
Задание 5. В задачах 5.1.-5.30. найти пределы функций.

5.1.

а)

lim

x3 +1

б)

lim

2 − x −1

2x2 + x −3

x→∞ x3 + x2

x→1

в)

lim

arcsin3x

г)

lim

x −1 x −1

;

x→0

x→∞

x +1

5.2.

а)

lim

x2 −2x +1

, б)

lim

x2 −3x + 2

3 − x −1

x→∞ x3 −5x2 + 2

x→2

в)

lim

sin6x

2x −1 4−x

г)

lim

;

x→0

x→∞

2x +3

5.3.а)

в)

5.4.а)

в)

5.5.а)

в)

5.6.а)

в)

5.7.а)

в)

5.8.а)

в)

5.9.а)

в)

5.10.а)

в)

lim

x→∞

lim

x→0

lim

x→∞

lim

x→0

lim

x→∞

lim

x→0

lim

x→∞

lim

x→0

lim

x→∞

lim

x→0

lim

x→∞

lim

x→0

lim

x→∞

lim

x→0

lim

x→∞

lim

x→0

x4 + 2x2 +1

б)

3x4 −5x3

+ x

tg3x

г)

x2 + 6x +1

б)

2x +1

arctg8x ,

г)

2x3 −1

б)

x3 + x2

sin10x

г)

tg2x

x2 +9x − 4

б)

2x2 +7x

12x

г)

arcsin3x

x5 −1

б)

2x4 + x2

14x

г)

sin2x

x6 − x3 +1

б)

2x6 + x3

16x

г)

tg2x

x7 +1

б)

2x + x7 ,

г)

arctg x

3x3 − 4x2 +1

б)

2x3 +5x

tg10x ,

г)

sin x

lim	x2 −2x −3			,
		3x −3
x→3
lim		3x + 2	5−9x		;
		3x +1
x→∞
lim	−x2 + 6x −8				,
		x −2
x→4
lim		4x −1 4x +3			;

		4x −5
x→∞

lim		x + 4 −3		,
	5 + 4x − x2
x→5
lim		5x +12 6−5x
					;
x→∞		5x +7
lim	x2 + 6x −72				,
	5 −		x +19
x→6
lim		6x +5 3x +5			;

x→∞		6x −7
lim		1−	x −6		,

x→7 x2 −5x −14
lim		7x −2 7x +11
					;
x→∞		7x −9
lim	x2 −9x +8			,
	2 −		x − 4
x→8
lim		8x −11 16x −5
					;
x→∞		8x −7
lim	x2 + x −90			,
	2 −		x −5
x→9
lim		9x + 21 5x +3
					;
x→∞		9x +3
lim		10x −10				,

x→10 x2 −11x +10
lim		10x −11 4−5x
					;
x→∞		10x +9

5.11.а)

в)

5.12.а)

в)

5.13.а)

в)

5.14.а)

в)

5.15.а)

в)

5.16.а)

в)

5.17.а)

в)

5.18.а)

в)

lim

x4 −2x3 +1

б)

lim

x2 −121

x +5 − 4

x→∞ 2x3 + x +7

x→11

lim

11arcsin x

lim

x −2 x −1

г)

;

x→0

x→∞

x +9

lim

x −8

б)

lim

x −8 −2

x −12

x→∞ 2x2 − x3

x→12

lim

sin24x

г)

lim

2x −9 4−2x

2x +3

;

x→0

x→∞

lim

x4 +1

, б)

lim

14x − x2 +13

14 − x −1

x→∞ x4 + x3 + 4x2

x→13

lim	13 tg3x	,	г)
x→0	3x

lim

x2 −1

б)

2x2 + x

x→∞

lim

7arctg2x

г)

x→0

lim

x3 + 4x +5

б)

x→∞ x3 + 2x2

lim

3sin5x

г)

x→0

tg x

lim

3x3 +5x +1

б)

2x3 + x2

x→∞

lim

16x

г)

x→0 arcsin x

lim

x2 −3x +1

б)

10x − x2

x→∞

lim

5x2

г)

x→0 1−cos x

lim

x3 +8

б)

x→∞ x2 −11x3

lim 18x ,

г)

x→0 tg x

lim	3x −14 5−3x
				;
x→∞	3x −1
lim	x + 2 − 4					,

x →14 x2 −15x +14
lim	4x −1 4x +3
				;
	4x +
x→∞		13
lim	4 −	x +1				,

x→15 x2 −16x +15
lim	5x +12 6−5x
				;
x→∞	5x −3
lim	x2 −14x −32					,
	x −12 −2
x→16
lim	6x +12 6x +5
				;
x→∞	6x − 4
lim	18 − x −1				,

x→17	18x − x2 −17
lim	7x +8 7x +11			;
	7x −
x→∞		9
lim	324 − x2
			,
	x −
x→18		2 − 4
lim	8x −5 16x −5			;
	8x +
x→∞		4

5.19.а)

в)

5.20.а)

в)

5.21.а)

в)

5.22.а)

в)

5.23.а)

в)

5.24.а)

в)

5.25.а)

в)

5.26.а)

в)

lim

x3 +12x

б)

12x2 + x +14

x→∞

lim

19x

г)

x→0 arctg x

lim

x2 − 4x +1

б)

5 −3x +

4x2

x→∞

lim

4 tg5x

г)

x→0

sin x

lim

x2 −7x +10

б)

5x + x2

x→∞

lim

7arcsin3x ,

г)

x→0

lim

x3 + 4x2 + 4x

б)

12x3 +

6x2

x→∞

lim 11sin2x

г)

x→0

lim

x4 + 2x −1

б)

+18

x→∞ x3 −7x2

lim

5 tg2 x

г)

x→0 1−cos x

lim

x2 +3x +5

б)

5x2 − 4x +

x→∞

lim

8arctg3x ,

г)

x→0

lim

x2 − 4x −21

б)

7x −3x2

x→∞

lim

5sin5x ,

г)

x→0

tg x

lim

2x3 + x +1

б)

x3 + x2

x→∞

lim

sin2 3x

г)

x→0

3x2

lim

x2 −21x +38

x −18 −1

x→19

lim

9x −22 3x +3

9x +

;

x→∞

lim

x2 −18x − 40

5 + x −5

x→20

lim

10x −21 4−5x

;

x→∞

10x +19

lim

25 − x − 2

24x − x2 − 63

x→21

lim

x −11 x −1

;

x→∞

x −10

lim

x2 −24x + 44

3 −

x −

x→22

lim

2x −8 6−4x

2x +

;

x→∞

lim

24 − x −1

22x − x2 + 23

x→23

lim

3x + 24 5−3x

;

x→∞

3x +1

lim

x +1 −5

x→24 x2 −23x −24

lim

4x +1 6x −4

;

x→∞

4x −5

lim

625 − x2

2x −1 −

x→25

lim

5x −12 2−5x

;

x→∞

5x −7

lim

2x2 + x −3

2 − x −1

x→1

lim

2x −1 x −1

;

2x +

x→∞

5.27. а)

lim

x2 − x +1

, б)

lim

x −2 −1

−3x + 2

x→∞ 2x3 +5x2 −2

x→2 x2

в)

lim

arcsin6x

г)

lim

x −1 4−x

;

x→0

x→∞

5.28.

а)

lim

2x4 + x2 +1

б)

lim

6 + x −3

x4 + x

x→∞

x→3 x2 −2x −

в)

lim

arctg3x

lim

x + 2 5−x

г)

;

x→0

x→∞

x +1

5.29.

а)

lim

3x2 + 6x −1

б)

lim −x2 + 6x −8

x→∞

2x +1

x→4

x +5 −3

в)

lim

tg8x

г)

lim

3x −1 x +3

;

x→0

x→∞

3x −5

5.30.

а)

lim

x3 + x −1

б)

lim

5 + 4x − x2

3x3 + x2 +1

x −1 −2

x→∞

x→5

в)

lim

sin x

г)

lim

3x +12 6−x

;

x→0 tg5x

x→∞

3x +7

Задание 6. В задачах 6.1.-6.30. найти производные y′x

функций:

6.1.

а)

y = 2x6 −

+ x2

x3 ,

б) y = ctg5 2x arccos x2,

в)

x =

y = ln(t −2),

г)

x − y + eyarctgx = 0;

−2

arctg3 2−x

6.2.

а)

y = x

−

б)

y =

x2 + x

в) x = t −1, y = 1 ,

г) y2x = ex ;

б) y = (sin x2 +1) arctg2 2x

6.3.

а)

y = 4x2 −

+ x5

в)

x =

cost

y =

sint

г) x4 + y4 = x2y2;

+ 2cost

1+ 2sint

6.4.

а)

y = x

7 −

б) y = cos3(3x) arctg(x3 ),

3 x

в)

x = tgt,

y =

г)

x − y2 + tg(x2y) = 0;

sin2t

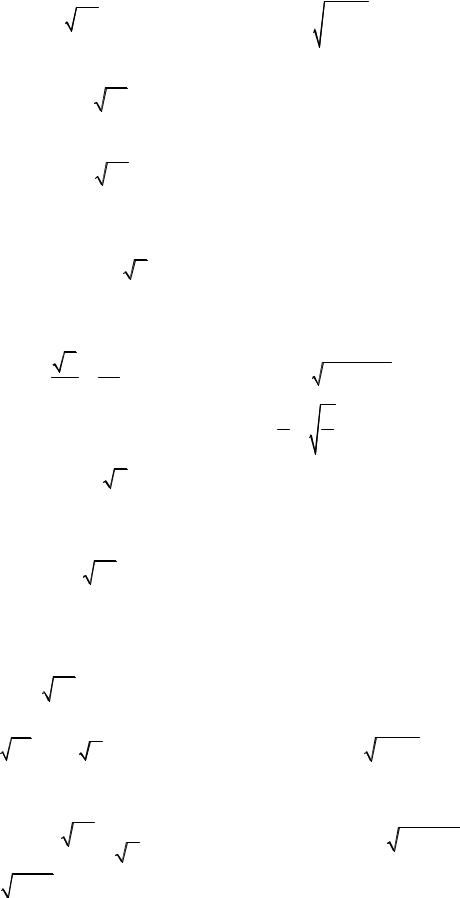
6.5.	а)	y =	1	−2x		x3 + 4x3,

			x2
	в)	x = 2(t −sint ), y = 4(2 + cost ),
6.6.	а)	y = x6 −			1	+ 2 6 x5 ,
					x6
	в)
		x = t + sint,				y = 2 +cost,

6.7.а) y = 4x3 − 2x + x 3 x2 ,

в) x = cost, y = lnsint,

6.8.	а) y = 2x3 −		1	+ 2x3 x,
		x3				πt

	в) x = 4 −sin		πt	, y = −4cos	2		,
			6			6

6.9.а) y = 4x3 − 7xx + x35 −5x,

в) x = 8sin

πt

y = −6cos πt

6.10.

а)

y = x4 −

+ x5

y = sin πt

в) x = 6 −cos

πt

−2,

6.11.

а)

y = 7 −

+ x3 x4 + x9,

πt

y = 4 −6cos πt

в) x = 2 −cos

6.12.

а)

y = x2 −

+5x ,

3 x4

в)

x = cost +t sint,

y = sint −t cost,

6.13.

а) y = 3 x2 +12x6 x − 4x3,

в)

x = cos2t,

y =

cos2 t

6.14.

а) y = x5 + x3

x2 −

5 x

в) x = 1−t2 , y =

б)

y = 3

x −3

x +3

б) exy + x2 + y3 = 2;

б)

y = sin2(3x) −cos x3,

г) ex + ey −2exy =1;

б)

ln(1+x2 )

y = 2

г)

−

1 y

+ ye

−

1 x

= 2;

б)

y =

tg x2

ln(x2 − 2x + 4)

г) x4 - x2y2 + y4 - 5x2 + 5y2 - 1= 0;

б) y = x4 −3x2 sin5x ,

г) yx − 3 xy = x;

б) y = lnsin2x tg(x + 2) ,

г) sin2(2x − y2 ) = 3x + 2;


б)	y = 2x2 sinln(x + 4);
г) x2 −3xy + y2 + x −5y = 0;
б)	y =		x3			;
			sin x	+
	2				1
г)	y2 cos x = sin(3x2 ) + y;
б)	y = arcsin					x ex ;
г) x3 +3xy2 +2y2 −5x =1;
б)	y = sin(ln x) 2x − x2 ,
г)	x	= tg(x2		− y);

	y

6.15.

а) y =

−

+ x

x6 ,

πt

в)

x = −2cos

πt

, y =

4 − 4sin

6.16.

а)

y = x8 +

− x4

x3 ,

в)

x = sht,

y = th2t,

6.17.

а) y = x3

x −

+ 3 ,

x x

в) x = t2 +t, y = 3 t −1,

6.18.

а)

y =

−3x3 + 2x

x7 ,

в) x = t3 −1, y = lnt,

6.19.

а) y =

x5 +

− x3 ,

3 x

в) x = t −1, y =

t −1

6.20.а) y = x2 − x52x +147 x ,

в) x = et , y = arcsint,

6.21.а) y = 2 1x3 −3x5 + 6x3 x ,

в) x = sint,	y =			1	,
			cost

6.22. а) y = x2 −	1	+		x2		− 4 ,
	2x3
				x3
в) x = cost + sint,				y = sin2t,

6.23.а) y = 4 − x3 x2 + x2 − x14 ,

в) x = cost, y = sin2 2t ,

6.24.а) y = 33 x2 − 2x + x−3 ,

в) x = cos2 t, y = tg2t,

б) y = ln(cos x) cos tg x ,

г) (x − y)2 +cos y2 = 4;

etgx

б) y = 2x +1,

г) x y + y3 cos x = 3;

б) y = ex2 −3x (x2 − x),

г) y2 = x2 − xln y +3;

б)	y =	ctg(3x2 + 2x)					,
б)	y =		ln x				,
			ln x
г) x2 ln y − y2 ln x =1;
б)	y =	earcsin x
б)	y =		x2 +	,
			x2 +	1
г)	y2 =		y − x	;
г)	y2 =		x + y	;
			x + y
б)	y =	8arctg(x +1)				,
			x2 − 4x + 4
г)	y2 sin x = cos(x − y);
б)	y =		e−cos x		,
б)	y =	ctg(2 x)			,
		ctg(2 x)

г) ln y = arctg yx ;

б)	y = ln	x2	−3x +1		,

		x2	+3x +1

г)	x2 + y2		= arctg	y		;
				x

б)	y = sin x2 (sin2 2x −1),

г) y2 + x2 −cos(x2 y2 ) = 2;

б) y = (sin6x −3x) x3 − x ,

г) tg yx = 5x +1;

1 / 21 2 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
25.12.20181.59 Mб18КП Женя.docx
#
24.09.20194.68 Mб3КП, Назарович Д..doc
#
20.09.2019849.56 Кб3Краткий курс лекций по статистики предприятия.docx
#
01.03.2016160.26 Кб21Криптосистема Хилла.doc
#
01.05.2019275.17 Кб9кристины курсавая 2012.docx
#
01.03.2016354.34 Кб9КР№1_задания на 2012 (осень).pdf
#
01.03.20162.64 Mб22Кр№2_АСОИ_ТМ_ТЭА_2008.doc
#
01.03.2016187.9 Кб17Кузьмич Зачет.doc
#
01.03.201641.5 Кб8культовое зодчество Брестской области.docx
#
22.12.2018149.5 Кб4культурология шпоры.doc
#
22.09.2019257.54 Кб9Культурология(шпоры).doc