метод Верещагина

= ;

;

= 

Проверка:

Расположим начало координат на левом конце балки, на опоре А (рис. 1)   

Прогиб на опоре А не существует, т.е. Y₀ = 0, чтобы определить ₀ запишем прогиб на опоре В, который также равен 0, при

;

  ;

Определяем  прогиб  в сечении К:

Сечение К переместится вниз.

Определяем угол поворота сечения К:

Сечение К повернулось по часовой стрелке.

2. Для  определения прогиба по интегралу Мора  необходимо рассмотреть единичную балку, приложив в сечении К,  (рис.1,б). Определяем для единичной балки опорные реакции   по формулам:

;

;

   

 ;

Запишем в пределах каждого участка  аналитические выражения

 изгибающих моментов от заданных нагрузок (грузовое состояние) и от  единичного момента.

Участок АК:                              Участок КС: ;                                       

;                                       

;                                                       

Участок СВ:   ;                                  Участок ДВ:  

           

                               

Определяем прогиб сечения К:     

Сечение К переместится по направлению единичной силы, т.е. вниз. Для определения угла поворота по интегралу Мора необходимо рассмотреть единичную балку, приложив  в сечении К момент, равный  = 1 (рис.1,в).

 Определяем для единичной балки опорные реакции   и : Условия статического равновесия и     дадут один результат:

Для рассмотренных ранее сечений Z запишем аналитическое выражение единичного момента.

Участок АК:                          Участок  КС: 

                                             

Участок СВ:                              Участок ДВ: 

                                                      

Определяем угол поворота сечения К:

            

 

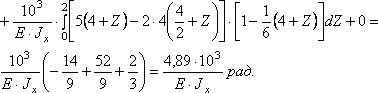
Сечение К  повернулось по направлению единичного момента, т.е. по часовой стрелке.

Для определения  перемещений способом Верещагина строим эпюры Q (рис. 2,б) и M (рис.2,в) для заданной балки.

Построение эпюры Q:

На участке АС в точке пересечения эпюры Q с нулевой линией на эпюре М будет максимум, найдем Z_1max:

На участке DB в точке пересечения эпюры Q с нулевой линией на эпюре М будет экстремум минимум. Найдем :

Построение эпюры М:  

Для определения прогиба сечения К строим эпюру  (рис.2, д) единичной балки, загруженной в сечении К силой,  равной  = 1 (рис. 2, г).

         

         .

Разобьем площадь грузовой эпюры на простые фигуры, площадь которых  можно легко определить.

Вычислим площади этих фигур    и определим  ординаты единичных моментов  под центром  тяжести каждой площади: 

                                                                                     Рис. 2

 

    

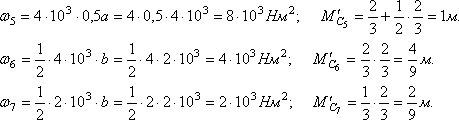
По формуле Верещагина определяем прогиб сечения К.

Сечение К переместилось по направлению единичной силы.

 

Для определения угла поворота сечения К строим эпюру (рис.2,и) для единичной балки, загруженной в сечении К моментом, равным  = 1 (рис.2,е):

  

;

.

Площади на грузовой эпюре вычислены выше. Определим ординаты единичных моментов , расположенные напротив центров тяжести каждой площади грузовой эпюры:

По формуле Верещагина определяем угол поворота сечения К:

Сечение К поворачивается по часовой стрелке  (по направлению единичного момента).

 

 

Задачи для самостоятельного решения

Задача 1.

Определить вертикальное перемещение у_А точки А консольной балки, изображенной на рисунке.

Ответ: y_A = 224Fl³/(Ed ⁴).

 

Задача 2.

Определить вертикальное перемещение у_В точки В консольной балки, нагруженной сосредоточенным моментом m на конце консоли (см. рис.). Балка имеет постоянную по длине жесткость на изгиб EI_z.

Ответ: y_B = ml²/(2EI_z).

 

Задача 3.

1) Определить вертикальное перемещение у_В точки В консольной балки, нагруженной равномерно распределенной нагрузкой q и с постоянной жесткостью на изгиб EI_z (рис. 1).

2) Определить вертикальное перемещение у_В  и угол поворота  точки В консольной балки с постоянной жесткостью EI на изгиб (рис. 2).

3) Определить вертикальное перемещение у_В  и угол поворота  точки В однопролетной балки с постоянной жесткостью EI на изгиб (рис. 3).

Ответ к рис.1: y_B = ql⁴/(8EI_z).

Ответ к рис.2: y_B = 3ml²/(2EI); = ml/(EI).

Ответ к рис.3: y_B = 0; = ml/(12EI).

 

Задача 4.

Определить вертикальное перемещение у_С  и угол поворота  точки С консольной балки с постоянной жесткостью EI_z на изгиб (см. рис.). Определить также у_А и  в точке А.

Ответ: = q[(a + b)³ – a³]/(6EI_z);     y_C = q{3(a + b)⁴ – 3a⁴ – 4a³b + 4c[(a + b)³ –a³]}/(24EI_z);

                 = qab(a + b)/(2EIz),    y_A = qa²b(4a + 3b)/(12EI_z).

 

Задача 5.

Определить максимальный прогиб консольной балки из электросварной прямошовной трубы с наружным диаметром D = 168 мм и толщиной стенки t = 6 мм, заделанной одним концом. Прогиб определить от действия собственного веса трубы. Длина консоли – 5 м. Проверить прочность консольной балки из стали С255, = 1.

Ответ: y_max = 0,9 см;= 24,7 МПа; = 0,8 МПа.

 

Задача 6.

Балка постоянного сечения АВС защемлена одним концом и загружена, как указано ниже на схемах. Определить прогибы и углы поворота в сечениях В и С методом Мора-Верещагина если: F = 20 кН; М₀ =40 кНм; q = 20 кН/м; b= 3 м; а = 2 м; Е = 2 МПа; 

 

Схема балки		Ответ:
а
б
в

 

Задача 7.

Определить прогибы в точках обозначенных буквой А, а также угол поворота сечений, обозначенных буквой В, если Е = 2 МПа.

	Схема балки	J в см4	Ответ:
			yA в см
а		1600	-1,6	-0,0107
б		4000	-1,237	-0,00769
в		2000	-0,5	+0,00333
г		2500	-0,96	+0,0096
д		3000	+1,611	+0,0164
е		3500	+0,667	-0,0076
ж		2500	-0,333	-0,00133
з		2500	+0,5	-0,04