
метод Верещагина
.docxЛекция 13 (продолжение). Примеры решения на вычисление перемещений методом Мора-Верещагина и задачи для самостоятельного решения
Определение перемещений в балках
Пример 1.
Определить перемещение точки К балки (см. рис.) при помощи интеграла Мора.

Решение.
1) Составляем уравнение изгибающего момента от внешней силы MF.
![]()
2) Прикладываем в точке К единичную силу F = 1.
3)
Записываем уравнение изгибающего
момента от единичной силы ![]() .
.
![]()
4) Определяем перемещения

Пример 2.
Определить перемещение точки К балки по способу Верещагина.

Решение.
1) Строим грузовую эпюру.
![]()
2) Прикладываем в точке К единичную силу.
3) Строим единичную эпюру.
![]()
4) Определяем прогиб
![]()
![]() ;
; ![]() ;
;
![]()
Пример 3.
Определить углы поворота на опорах А и В для заданной балки (см. рис.).
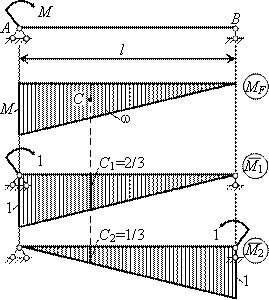
Решение.
Строим эпюры от заданной нагрузки и от единичных моментов, приложенных в сечениях А и В (см. рис.). Искомые перемещения определяем с помощью интегралов Мора
![]() ,
,
![]() , которые вычисляем
по правилу Верещагина.
, которые вычисляем
по правилу Верещагина.
Находим параметры эпюр
![]() C1 =
2/3, C2 =
1/3,
C1 =
2/3, C2 =
1/3,
а затем и углы поворота на опорах А и В
![]()
![]()
Пример 4.
Определить угол поворота сечения С для заданной балки (см. рис.).

Решение.
Определяем
опорные реакции ![]() RA=RB,
RA=RB,
![]() ,
, ![]() , RA = RB = qa.
, RA = RB = qa.
Строим
эпюры изгибающего момента от заданной
нагрузки и от единичного момента,
приложенного в сечении С,
где ищется угол поворота. Интеграл Мора
вычисляем по правилу
Верещагина. Находим параметры эпюр ![]()
![]() C2 =
-C1 =
-1/4,
C2 =
-C1 =
-1/4,
а по ним и искомое перемещение
![]() .
.
Пример 5.
Определить прогиб в сечении С для заданной балки (см. рис.).

Решение.
1. Построение эпюр изгибающих моментов.
Эпюра MF (рис. б)
Опорные реакции:
ВЕ: ![]() ,
, ![]() ,
,
![]() , RB + RE = F, RE =
0;
, RB + RE = F, RE =
0;
АВ: ![]() , RА = RВ = F;
, RА = RВ = F; ![]() ,
, ![]() .
.
Вычисляем
моменты в характерных точках ![]() , MB =
0, MC = Fa и строим эпюру изгибающего
момента от заданной нагрузки.
, MB =
0, MC = Fa и строим эпюру изгибающего
момента от заданной нагрузки.
Эпюра ![]() (рис.
в).
(рис.
в).
В
сечении С,
где ищется прогиб, прикладываем единичную
силу ![]() и
строим от нее эпюру изгибающего момента,
вычисляя сначала опорные
реакции ВЕ -
и
строим от нее эпюру изгибающего момента,
вычисляя сначала опорные
реакции ВЕ - ![]() ,
, ![]() ,
, ![]() =
2/3;
=
2/3; ![]() ,
, ![]() ,
, ![]() =
1/3, а затем моменты в характерных
точках
=
1/3, а затем моменты в характерных
точках ![]() ,
, ![]() ,
, ![]() .
.
2.
Определение искомого прогиба. Воспользуемся
правилом Верещагина и вычислим
предварительно параметры эпюр ![]() и
и ![]() :
:
![]()
![]()
![]() ,
,
![]()
![]()
![]()
Прогиб сечения С
![]() .
.
Пример 6.
Определить прогиб в сечении С для заданной балки (см. рис.).
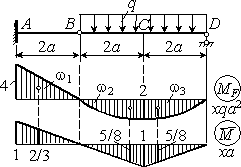
Решение.
Строим
эпюры изгибающих моментов от заданной
нагрузки и от единичной силы, приложенной
в точке С. Пользуясь
правилом Верещагина, вычисляем параметры
эпюр ![]()
![]() ,
,
![]()
![]()
и находим искомый прогиб
![]() .
.
Пример 7.
Определить прогиб в сечении С для заданной балки (см. рис.).

Решение.
1. Построение эпюр изгибающих моментов.
Опорные реакции:
![]() ,
, ![]() , RA =
2qa,
, RA =
2qa,
![]() , RA + RD =
3qa, RD = qa.
, RA + RD =
3qa, RD = qa.
Строим эпюры изгибающих моментов от заданной нагрузки и от единичной силы, приложенной в точке С.
2. Определение перемещений. Для вычисления интеграла Мора воспользуемся формулой Симпсона, последовательно применяя ее к каждому из трех участков, на которые разбивается балка.
Участок АВ: ![]()
![]()

Участок ВС: ![]()
![]()
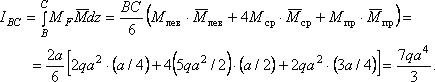
Участок СD: ![]()
![]()
![]()
Искомое перемещение
![]() .
.
Пример 8.
Определить прогиб сечения А и угол поворота сечения Е для заданной балки (рис. а).

Решение.
1. Построение эпюр изгибающих моментов.
Эпюра МF (рис. в). Определив опорные реакции
![]() ,
, ![]() , RB =
19qa/8,
, RB =
19qa/8,
![]() , RD =
13qa/8,
строим эпюры поперечной силы Q и
изгибающего момента МF от
заданной нагрузки.
, RD =
13qa/8,
строим эпюры поперечной силы Q и
изгибающего момента МF от
заданной нагрузки.
Эпюра ![]() (рис.
д). В сечении А,
где ищется прогиб, прикладываем единичную
силу и строим от нее эпюру изгибающего
момента.
(рис.
д). В сечении А,
где ищется прогиб, прикладываем единичную
силу и строим от нее эпюру изгибающего
момента.
Эпюра ![]() (рис.
е). Эта эпюра строится от единичного
момента, приложенного в сечении Е,
где ищется угол поворота.
(рис.
е). Эта эпюра строится от единичного
момента, приложенного в сечении Е,
где ищется угол поворота.
2. Определение перемещений. Прогиб сечения А находим, пользуясь правилом Верещагина. Эпюру МF на участках ВС и CD разбиваем на простые части (рис. г). Необходимые вычисления представляем в виде таблицы.
|
Номер части |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
|
-qa3/6 |
2qa3/3 |
-qa3/2 |
qa3/4 |
qa3/4 |
-qa3 |
-qa3/2 |
|
|
Ci |
-3a/4 |
-3a/4 |
-5a/6 |
-2a/3 |
-a/3 |
-a/6 |
0 |
|
|
|
qa4/8 |
-qa4/2 |
5qa4/12 |
-qa4/6 |
-qa4/12 |
qa4/6 |
0 |
-qa4/24 |
Получаем ![]() .
.
Знак “минус” в результате означает, что точка А перемещается не вниз, как была направлена единичная сила, а вверх.
Угол поворота сечения Е находим двумя способами: по правилу Верещагина и по формуле Симпсона.
По
правилу Верещагина, перемножая
эпюры MF и ![]() ,
по аналогии с предыдущим получим
,
по аналогии с предыдущим получим
![]() ,
,
![]() .
.
Для нахождения угла поворота по формуле Симпсона вычислим предварительно изгибающие моменты посредине участков:
![]()
![]()
![]()
Искомое перемещение, увеличенное в EIx раз,
![]()
![]() .
.
Пример 9.
Определить, при каком значении коэффициента k прогиб сечения С будет равен нулю. При найденном значении k построить эпюру изгибающего момента и изобразить примерный вид упругой линии балки (см. рис.).

Решение.
Строим эпюры изгибающих моментов от заданной нагрузки и от единичной силы, приложенной в сечении С, где ищется прогиб.
По
условию задачи VC =
0. С другой стороны, ![]() .
Интеграл на участке АВ вычисляем
по формуле Симпсона, а на участке ВС –
по правилу Верещагина.
.
Интеграл на участке АВ вычисляем
по формуле Симпсона, а на участке ВС –
по правилу Верещагина.
Находим предварительно
![]()
Перемещение
сечения С ![]() ,
,

Отсюда ![]() ,
, ![]() .
.
При
найденном значении k определяем
значение опорной реакции в
точке А: ![]() ,
, ![]() ,
, ![]() ,
исходя из которого находим положение
точки экстремума на эпюре М согласно
условию
,
исходя из которого находим положение
точки экстремума на эпюре М согласно
условию ![]() .
.
По значениям момента в характерных точках
![]() ,
, ![]() ,
, ![]()
строим эпюру изгибающего момента (рис. г).
Пример 10.
Определить вертикальное перемещение точки В консольной балки, изображенной на рисунке.
![]()

Решение.
Строим эпюру изгибающих моментов М от действия внешней сосредоточенной силы F: МВ = 0, МА = –F2l (эпюра линейная).
По
условию задачи требуется определить
вертикальное перемещение уВ точки В консольной
балки, поэтому строим единичную эпюру ![]() от
действия вертикальной единичной
силы Fi =
1, приложенной в точке В.
от
действия вертикальной единичной
силы Fi =
1, приложенной в точке В.
Учитывая,
что консольная балка состоит из двух
участков с разной жесткостью на изгиб,
эпюры ![]() и М перемножаем
с помощью правила Верещагина по участкам
отдельно. Эпюры М и
и М перемножаем
с помощью правила Верещагина по участкам
отдельно. Эпюры М и![]() первого
участка перемножаем по формуле
первого
участка перемножаем по формуле ![]() ,
а эпюры второго участка – как площадь
эпюры М второго
участка Fl2/2
на ординату 2l/3
эпюры
,
а эпюры второго участка – как площадь
эпюры М второго
участка Fl2/2
на ординату 2l/3
эпюры ![]() второго
участка под центром тяжести треугольной
эпюры М этого
же участка.
второго
участка под центром тяжести треугольной
эпюры М этого
же участка.
В
этом случае формула ![]() дает:
дает:
![]()
Пример 11.
Определить вертикальное перемещение точки В однопролетной балки, изображенной на рисунке. Балка имеет постоянную по всей длине жесткость на изгиб EI.
![]()
![]()
![]()

Решение.
Строим эпюру изгибающих моментов М от действия внешней распределенной нагрузки: МА = 0; MD = 0;
![]() .
.
Прикладываем
в точке В единичную
вертикальную силу Fi = 1
и строим эпюру ![]() (см.
рис.):
(см.
рис.):
![]() откуда Ra =
2/3;
откуда Ra =
2/3;
![]() откуда Rd =
1/3, поэтому Ma =
0; Md =
0;
откуда Rd =
1/3, поэтому Ma =
0; Md =
0; ![]() .
.
Разделим
рассматриваемую балку на 3 участка.
Перемножение эпюр 1-го и 3-го участков
не вызывает трудностей, так как перемножаем
треугольные эпюры. Для того чтобы
применить правило Верещагина ко 2-му
участку, разобьем эпюру М 2-го
участка на две составляющие эпюры:
прямоугольную и параболическую с
площадью ![]() (см.
таблицу).
(см.
таблицу).
|
|
|
|
|
|
Центр тяжести параболической части эпюры М лежит посередине 2-го участка.
Таким
образом, формула ![]() при
использовании правила Верещагина дает:
при
использовании правила Верещагина дает:
![]()
Пример 12.
Определить максимальный прогиб в двухопорной балке, нагруженной равномерно распределенной нагрузкой интенсивности q (см. рис.).
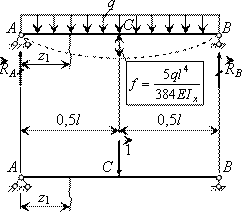
Решение.
Находим изгибающие моменты:
- от заданной нагрузки
![]()
-
от единичной силы, приложенной в точке С,
где ищется прогиб ![]() .
.
Вычисляем искомый наибольший прогиб, который возникает в среднем сечении балки
![]()
Пример 13.
Определить прогиб в точке В балки, показанной на рисунке.

Решение.
Строим эпюры изгибающих моментов от заданной нагрузки и единичной силы, приложенной в точке В. Чтобы перемножить эти эпюры, надо балку разбить на три участка, так как единичная эпюра ограничена тремя различными прямыми.
Операция перемножения эпюр на втором и третьем участках осуществляется просто. Затруднения возникают при вычислении площади и координат центра тяжести основной эпюры на первом участке. В таких случаях намного упрощает решение задачи построение расслоенных эпюр. При этом удобно одно из сечений принять условно за неподвижное и строить эпюры от каждой из нагрузок, приближаясь справа и слева к этому сечению. Целесообразно за неподвижное принимать сечение в месте перелома на эпюре единичных нагрузок.
Расслоенная эпюра, в которой за неподвижное принято сечение В, представлена на рисунке. Вычислив площади составных частей расслоенной эпюры и соответствующие им ординаты единичной эпюры, получаем
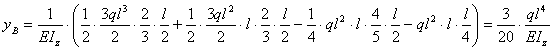 .
.
Пример 14.
Определить перемещения в точках 1 и 2 балки (рис. а).

Решение.
Приведем
эпюры М и Q для
балки при а=2
м; q=10
кН/м; С=1,5а; М=0,5qa2; Р=0,8qa; М0=М; ![]() =200
МПа (рис. б и в).
=200
МПа (рис. б и в).
Далее определяем перемещения в точках 1 и 2 балки (рис. а). Состояние балки под действием заданной нагрузки обозначим q.
Определим
вертикальное перемещение ![]() центра
сечения, где приложен сосредоточенный
момент. Для этого рассмотрим балку
в состоянии
центра
сечения, где приложен сосредоточенный
момент. Для этого рассмотрим балку
в состоянии ![]() под
действием только сосредоточенной
силы
под
действием только сосредоточенной
силы ![]() приложенной
в точке 1 перпендикулярно оси балки (по
направлению искомого перемещения
приложенной
в точке 1 перпендикулярно оси балки (по
направлению искомого перемещения ![]() )
(рис. г).
)
(рис. г).
Вычислим опорные реакции, составив три уравнения равновесия
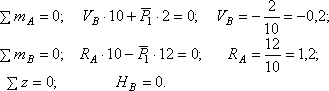
Проверка ![]()
Реакции найдены верно.
Для
построения эпюры ![]() рассмотрим
три участка (рис. г).
рассмотрим
три участка (рис. г).
1 участок
![]()
2 участок
![]()

3 участок
![]()
По
этим данным строим эпюру ![]() (рис.
д) со стороны растянутых волокон.
(рис.
д) со стороны растянутых волокон.
Определим ![]() по
формуле Мора с помощью правила Верещагина.
При этом криволинейную эпюру
по
формуле Мора с помощью правила Верещагина.
При этом криволинейную эпюру ![]() ,
на участке между опорами, можно представить
в виде сложения трех эпюр. Стрелка
,
на участке между опорами, можно представить
в виде сложения трех эпюр. Стрелка
![]()
![]()
![]()
Знак
«минус» означает, что точка 1 перемещается
вверх (в направлении противоположном ![]() ).
).
Определим
вертикальное перемещение ![]() точки
2, где приложена сосредоточенная сила.
Для этого рассмотрим балку в состоянии
точки
2, где приложена сосредоточенная сила.
Для этого рассмотрим балку в состоянии ![]() под
действием только сосредоточенной
силы
под
действием только сосредоточенной
силы ![]() приложенной
в точке 2 перпендикулярно оси балки (по
направлению искомого перемещения
приложенной
в точке 2 перпендикулярно оси балки (по
направлению искомого перемещения ![]() )
(рис. е).
)
(рис. е).
Эпюра ![]() строится
аналогично предыдущей.
строится
аналогично предыдущей.
Далее по формуле Мора
![]()
![]()
Точка 2 перемещается вверх.
Определим
угол поворота ![]() сечения,
где приложен сосредоточенный момент.
сечения,
где приложен сосредоточенный момент.

