Статика(Мои задачи) @

Задача С2. Груз весом Р (н), поднимаемый краном АВС, удерживается в равновесии

при помощи каната, перекинутого через блок А и закрепленного в точке D неподвижно. Определить реакции в шарнирах В и С, если крепления в точках А, В и С шарнирные, углы α и β заданы, а весом стержней АВ и АС пренебречь (рис. 2, табл. 2).

Рис.2

Задача С7. Балка АВ весом Р(н) концом А закреплена при помощи неподвижного цилиндрического шарнира, а другим концом В опирается на гладкую наклонную плоскость. К балке АВ приложена пара сил с моментом М (нм). В точке D к балке АВ прикреплена веревка, перекинутая через блок Е, к концу которой подвешен груз весом Q (н). Определить реакции опор в точках А и В, если длина балки АВ, а также АС и AD (в метрах) заданы (рис. 7, табл.7).

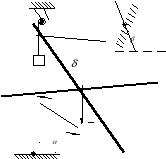
Рис.7

Задача С14. Определить реакции в опорных шарнирах А и В и в соединительном шарнире С составной рамы, возникающие под действием сил P₁ и P₂ (Кн), равномерно распределенной нагрузки интенсивности q (кн/м), действующей на участке СD = b,и пары сил с моментом M (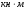), приложенной к левой части АЕС рамы как показано на рис. 14. Длины AE=a, EC=CD=b, DB=c,DL=e,AK=d (м) и углы α,β,φ заданы (рис.14,табл.14).

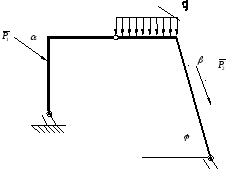
Рис. 14

Задача С16. К ферме приложены пять заданных сил P₁, P₂, P₃, P₄, P₅. Определить опорные реакции в точках А и В. Найти также усилия в стержнях 1, 2, 3 способом Риттеpa, а в стержнях 4 и 5 —по способу вырезания узлов (табл. 16; силы заданы в килоньютонах, расстояния в метрах). Варианты нагружения : 1) рис. 16; 2) рис. 17; 3) рис. 18; 4) рис. 19; 5) рис. 20.

Задача С17. Система шести невесомых стержней имеет три неподвижные опоры С, D и О и два соединительных шарнира А и В, как указано на рисунке. В узлах А и В приложены заданные силы Р и Q (Кн), причем сила Р лежит в плоскости zАу и составляет с осью Ау угол φ, а сила Q составляет с осями координат х, у, z углы α,β,γ. Определить усилия в этих стержнях, если заданы углы,β,, φ. Исходные данные: для рис. 21, табл. 17; для рис, 22, табл. 18.

Рис. 21

Задача С22. Груз весом Q н поднимается равномерно при помощи ворота. Рукоятка АЕ =а и приложенная к ней сила P лежат в плоскости, перпендикулярной к оси АВ ворота, причем сила Р составляет с вертикалью угол γ. Верёвка сходит с барабана под углом α к горизонтали. К колесу D, жестко скрепленному с воротом, приложена пара сил с моментом m нм. Определить силу Р и реакции подшипников А и В, если известны расстояние АЕ = a, радиус барабана R (в сантиметрах) и отношение AC/AB=k (рис. 28, табл. 24).

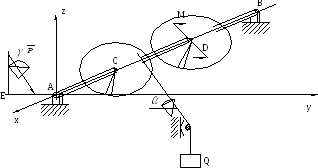
Рис. 28

y

x

z

A

C

D

B

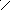
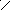
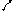
E

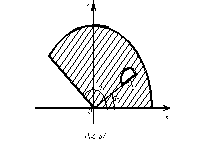
Задача С29. Из однородного кругового сектора радиуса R с центральным углом

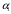
вырезан полукруг радиуса r с центром О₁, причем ÐxOO₁= . Определить координаты центра тяжести оставшейся части, если известны отношения OO₁/R=m, r/R=n (рис. 37, табл. 32).

Задача К1. Найти уравнение траектории, скорость и ускорение точки, если движение этой точки задано уравнениями в декартовых координатах: x=f₁(t),y=f₂(t).

Кроме того, построить положения этой точки и вычислить ее скорость, полное, нормальное, касательное ускорения и радиус кривизны траектории для момента t₁; показать на рисунке вид траектории, вектор скорости и ускорения по их составляющимV_X ,V_Y, a_x, a_y, a_t, a_n в масштабе (табл. 34 — 38), где х и у заданы в сантиметрах, а t — в секундах.

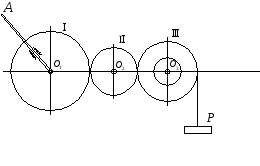
Задача К6. Три колеса I, II, III с радиусами r₁=20 см, r₂ = 5 см, r₃=15 см, вращающиеся вокруг неподвижных осей O₁, O₂ и O₃, сцеплены между собой, как показано на рис. 42. К колесу I жестко прикреплена рукоятка длиною O₁А = , а на вал радиуса r₄=10 см, жестко скрепленный с колесом III, намотана веревка, к концу которой подвешен груз Р.

Зная закон движения груза x = f(t), определить в момент t₁ в вариантах 2, 4, 6, 8, 10 угловую скорость и угловое ускорение колеса II, а также скорость и ускорение конца А рукоятки, а в вариантах 1, 3, 5, 7, 9 определить угловую скорость и угловое ускорение рукоятки и скорость и ускорение точки, лежащей па ободе колеса II. Ось Ох направлена по вертикали вниз (рис. 42, табл. 47; х и а заданы в сантиметрах, a t — в сек).

Р