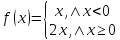Дополнительные задания

1. Найдите все линейные функции , такие, что функция совпадает с обратной по отношению к ней функцией.

Ответ. .

2. Постройте график функции, обратной данной. Найдите формулу, задающую обратную функцию.

3. Функция обратима. Известно, что уравнение имеет следующие корни . Решить уравнение , где функция, обратная к .

Ответ. .

4. Функция имеет обратную функцию . Решить уравнение , если известно, что уравнение имеет корни .

Ответ. .

5. Докажите, что если - возрастающая (убывающая) функция, то и обратная к ней функция так же является возрастающей (убывающей) функцией.

6. Верно ли, что если нечетная функция имеет обратную функцию, то она также будет нечетной?

Ответ. Верно

7. Может ли функция, обратная к данной функции, быть четной функцией?

Ответ. Не может

8. Найдите функцию, обратную функции , и постройте ее график.

		Ответ

Раздаточный материал

Обратная функция

Упражнения

1. Укажите, на каких рисунках изображены графики обратимых функций.

2. Функции имеет два нуля. Почему она не имеет обратной функции?

3. На рисунке изображен график обратимой функции . Найдите значения обратной к ней функции при значениях аргумента равных 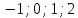. Укажите область определения и множество значений обратной функции.

4. Найдите функцию, обратную по отношению к линейной функции

5. Нарисуйте график какой-нибудь обратимой функции , ( – обратная к ней), так, чтобы были выполнены следующие условия

6. Функция имеет обратную. Найдите область определения и множество значений обратной функции, если известно, что:

1.	2.
3.	4.

7. Функция задана графиком. Построить график обратной к ней функции

8. Найдите функцию , которая является обратной по отношению к функции

	.
	.
	.

Д. / з.

9. Найдите функцию, обратную функции , и постройте ее график.

10. Постройте график функции, обратной данной.
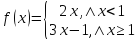