7. Пример 2. Докажите, что функция является обратимой. Найдите обратную к ней функцию.

Решение. Построим график заданной функции – часть параболы (рис.10), которая удовлетворяет условию .

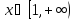
Заданная функции является возрастающей а, следовательно, и обратимой. Для нахождения обратной к ней функции нужно из уравнения выразить х через у, а затем ввести новые обозначения переменных.

Запишем уравнение в виде . Это квадратное уравнение относительно неизвестного , свободный член уравнения равен . Найдем дискриминант квадратного уравнения , . По формуле корней квадратного уравнения имеем или, после упрощения . Итак при любом допустимом значении квадратное уравнение имеет два корня и . Учитывая, что область определения заданной функции - промежуток, получаем .

Переобозначив переменные, то есть поменяв их местами, получаем формулу обратной функции .

Замечание. Фактически мы доказали, что если рассматривать функцию на промежутке , то на этом промежутке она является обратимой, поскольку возрастает. При этом, функция не обратима, если она рассматривается на (рис.10). На промежутке , функция убывает, а значит обратима.

Графики рассмотренной в примере функции и обратной к ней изображены на рисунке 15. Следует отметить тот факт, что они пересекаются в точке, принадлежащей прямой . Это не случайно. Действительно, пусть график обратимой функции имеет общую с прямой точку . Тогда, точка, симметричная точке относительно этой прямой, принадлежит графику обратной функции .Но этой точкой является сама точка . Значит, она принадлежит обоим графикам одновременно, то есть является их точкой пересечения.

Упражнения

1. Укажите, на каких рисунках изображены графики обратимых функций.

Ответ. 4;6

2. Функции имеет два нуля. Почему она не имеет обратной функции?

3. На рисунке изображен график функции . Докажите,

что она не имеет обратной функции. Определите числовой промежуток на оси ординат, такой, что новая функция – обратима. Укажите несколько возможных вариантов .

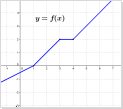
4. На рисунке изображен график обратимой функции . Найдите значения обратной к ней функции при значениях аргумента равных . Укажите область определения и множество значений обратной функции.

Ответ.

1)

2)

5. Найдите функцию, обратную по отношению к линейной функции

		Ответ

6. Нарисуйте график какой-нибудь обратимой функции , ( – обратная к ней), так, чтобы были выполнены следующие условия

7. Функция имеет обратную. Найдите область определения и множество значений обратной функции, если известно, что:

1.	2.
3.	4.

9. Функция задана графиком. Построить график обратной к ней функции

8. Найдите функцию , которая является обратной по отношению к функции

		Ответ
	.
	.
	.
		,