3. Ветровая нагрузка.

Нормативный скоростной напор ветра для Vветрового района

Коэффициент, учитывающий изменение ветра по высоте для типа местности на высоте

Расчётная линейно распределённая ветровая нагрузка от активного давления на высоте

где аэродинамический коэффициент для активного давления (для отсоса).

4. Статический расчёт поперечной рамы.

Рис. 4. Расчётная схема рамы.

Момент инерции нижней части колонны приближённо равен:

Момент инерции верхней части колонны:

Рассматривается 8 загружений рамы:

1 – постоянная нагрузка на ригель рамы;

2 – снеговая нагрузка на ригель рамы;

3 – вертикальная крановая нагрузка на левой колонне ина правой колонне;

4 – то же, справа ислева;

5 – сила поперечного торможения крана на левой колонне (действует слева направо или справа налево);

6 – тоже, сила на правой колонне;

7 – ветер слева (напор на левой стойке, отсос на правой);

8 – ветер справа;

Расчётная схема рамы с действующими на неё нагрузками показана на рис. 4.

Статический расчёт рамы выполняется по программе “KLOT” . Исходные данные, необходимые для расчёта на ЭВМ, приводятся в таблице 3.

№ п/п	Данные для расчёта	Обозначение	Числовые значения
1	Шифр задачи (Ф.И.О. студента, № группы)		ГрадовичР.С. П-304
2	Пролёт в осях поперечной рамы в м (24, 30, 36)		24
3	Ширина нижней части колонны в м		1.25
4	Ширина верхней части колонны в м		0.4
5	Привязка колонны к разбивочной оси в м		0.25
6	Высота нижней части колонны в м		11.18
7	Высота верхней части колонны в м		4.02
8	Заглубление колонны ниже пола в м		0.8
9	Высота стропильной фермы в м		2.19
10	Высота подкрановой балки в м		0,7
11	Постоянная погонная нагрузка на ригель в кН/м		19.785
12	Снеговая погонная нагрузка на ригель в кН/м		6,384
13	Ветровая активная погонная нагрузка на отм. 10 м в кН/м		2.50
14	Тип местности по ветровой нагрузке (А, В, С)		B
15	Максимальное вертикальное давление крана в кН		553.44
16	Минимальное вертикальное давление крана в кН		166.67
17	Поперечное горизонтальное торможение крана в кН		18,014

5. Расчёт и конструирование ступенчатой колонны.

1. Расчётные усилия в колонне.

По результатам статического расчёта для верхней части колонны из двух расчётных сечений (3-3 и 4-4) выбирается сочетание нагрузок с максимальными абсолютными значениями изгибающего момента и продольной силы. Для нижней части колонны из расчётных сечений (1-1 и 2-2) выбирается два сочетания нагрузок с максимальными абсолютными значениями изгибающего моментаи продольной силы, при этом одно сочетание – с отрицательным изгибающим моментом (момент догружает подкрановую часть колонны), второе сочетание – с положительным изгибающим моментом (момент догружает наружную ветвь колонны).

Если абсолютное значение больше в одном сочетании, а абсолютное значениебольше в другом сочетании, то для выявления расчётного сочетания рекомендуется определить величину, гдевысота сечения верхней или нижней части колонны. За расчётное следует принять то сочетание, в которомбудет наибольшим.

Расчётные комбинации усилий в колонне:

1. Для верхней части колонны в сечении 4-4:

(1, 4, 6, 8, 2)

в сечении 3-3 при том же сочетании нагрузок получим:

2. Для нижней части колонны

Для М со знаком «+»:

(1, 4, 5, 8, 2)

(1, 2, 3, 5, 8)

Для М со знаком «-»:

(1, 3, 5, 7)

(1, 2, 3, 5, 7)

(1, 3, 5)

(сечение 1–1) (1, 3, 5, 7)

(сечение 1–1) (1, 2, 3, 5, 8)

максимальная поперечная сила

В дальнейших расчётах знаки усилий можно опустить.

2. Расчётные длины колонны.

Расчетные длины для верхней и нижней частей колонны в плоскости рамы определяем по формулам и , где .

Коэффициенты иопределяются в зависимости от параметровипо таблице 68 [1].

Соотношение погонных жесткостей верхней и нижней частей колонны

где соотношение усилий в нижней и верхней части колонны.

Для однопролётной рамы с жёстким сопряжением ригеля с колонной (верхний конец колонны закреплён только от поворота) по таблице 68 [1] ..

Таким образом, для нижней части колонны

для верхней части колонны

Расчётные длины из плоскости рамы для нижней и верхней частей колонны равны соответственно:

3. Подбор сечения верхней части колонны.

Верхнюю часть колонны принимаем из сварного двутавра высотой . Из условия устойчивости определяем требуемую площадь сечения. Для симметричного двутавра:

Условная гибкость стержня ,

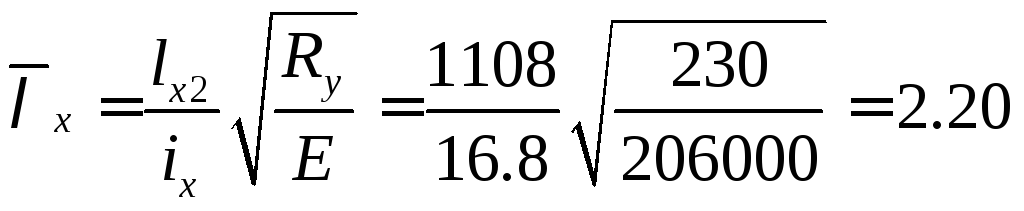где для листового проката толщиной 10 – 20 мм из стали класса С235.

Относительный эксцентриситет .

Примем приближённо , тогда коэффициент влияния формы сечения (табл. 73 [1]) . Приведенный относительный эксцентриситет.

По таблице 74 [1] при икоэффициент.

Коэффициент условий работы для колонны .

Предварительно толщину полки принимаем .

Тогда высота стенки .

Определяем требуемую толщину стенки из условия её местной устойчивости при изгибе колонны в плоскости действия момента . Предельная условная гибкость стенки прии(табл. 27^*[1]).

Требуемая толщина стенки . Принимаем.

В дальнейших расчётах вместо будем приниматьи вместо.

Требуемая площадь и ширина полки

Из условия устойчивости верхней части колонны из плоскости действия момента ;.

Из условия местной устойчивости полки ,где

Принимаем (рис. 5).

Рис. 5. Сечение колонны.

Вычисляем геометрические характеристики сечения.

Полная площадь сечения .

Расчётная площадь сечения с учётом только устойчивой части стенки равна полной площади сечения, т.к. ,.

.

.

..

..

Проверяем устойчивость верхней части колонны в плоскости действия момента. Гибкость колонны ;Т.к.незначительно отличается от предварительнопринятой, то расчётную высоту стенкиможно не уточнять.

Относительный эксцентриситет .

Так как , то коэффициент

(табл. 73 [1]),(табл. 74 [1]).

Недонапряжение

Гибкость колонны в плоскости рамы не превышает допустимой , где.

Проверяем устойчивость верхней части колонны из плоскости действия момента. Гибкость колонны . Коэффициент продольного изгиба(табл. 72 [1]).

Максимальный момент в средней трети расчётной длины стержня

По модулю

Относительный эксцентриситет .

При (табл. 10 [1]),.

Так как , то.

.

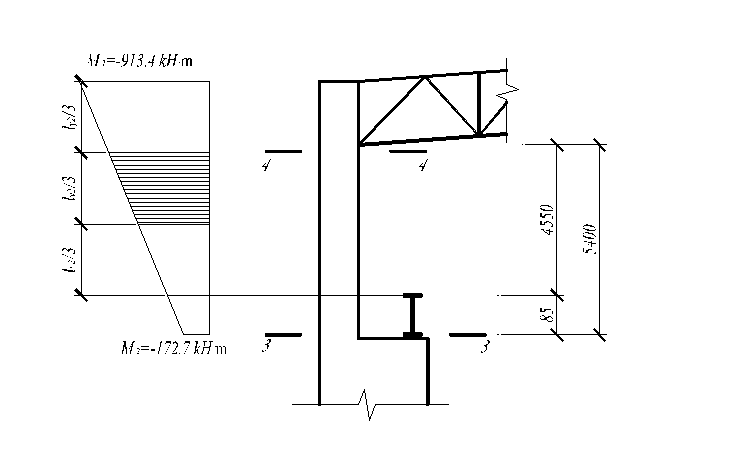
Рис. 6. К определению расчётного момента .

Гибкость колонны из плоскости рамы не превышает предельно допустимой , где.

Проверяем местную устойчивость полки колонны. Свес полки .

Так как: , то местная устойчивость полки обеспечена.

Проверяем местную устойчивость стенки при изгибе колонны из плоскости действия момента. Наибольшие сжимающие напряжения на краю стенки:

Недонапряжение

Напряжения на противоположном краю стенки:

Средние касательные напряжения в стенке:

Коэффициент (с учётом знакови).

При наибольшее отношениеопределяем по формуле

,

где . Принимаем.

Так как , то местная устойчивость обеспечена.

При стенку не требуется укреплять поперечными рёбрами жёсткости, расположенными на расстоянии, но не менее двух ребер в рпеделах верхней части колонны.

Ширина парных симметричных ребер Принимаем ширину рёберb_h=60 мм. Толщину ребер. Принимаемt_s=5 мм.