§13. Закон сохранения энергии в электромагнитном поле.

Рассмотрим замкнутую систему, состоящую из поля и частиц. Найдем работу W,произведение силами поля над частицами, находящиеся в объеме V. Относя эту работу W к единице времени t и считая заряды непрерывно распределенные в пространстве и пользуясь формулой плотности для силы Лоренца можем написать:

(1)

Учитывая, что

Преобразуем формулу (1) к следующему виду:

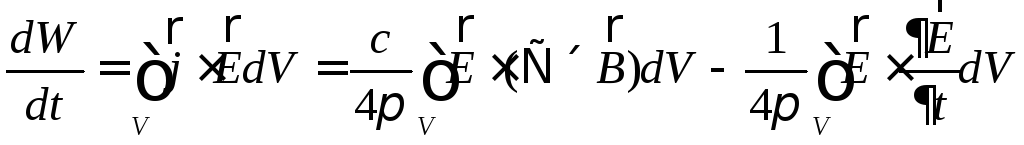(2)

Добавим к формуле (2) равную величину :

( Первое уравнение Максвелла)

и получим:

(3)

Используя векторное тождество:

Преобразуем первый интеграл в (3) к поверхностному.

(4)

Рассмотрим случай, когда . ЕслиE и B стремится к нулю, при быстрее, чем по закону, то поверхностный интеграл обращается в ноль.

быстрее, чем . А величина поверхности растет как. Следовательно (4) переходит в выражение :(5),

где (6)

Поскольку в левой части (5) стоит работа в единицу времени t, то правая – убыль энергии в единицу времени t. Естественно полагать ,что в замкнутой системе, состоящей из поля и частиц , работа, производимая электромагнитным полем над частицами равна убыли энергии самого поля. При этом полю необходимо приписать энергию, плотность которой выражается формулой (6). Выражениенельзя свести к величинам, определяющимся только взаимным расположением и движением зарядов. Следовательно и нельзя считать потенциальную энергию взаимодействующих частиц. Плотность энергии, в частности, отлично от нуля в той области пространства, которая свободна от частиц. Наличие у электромагнитного поля энергии показывает, что оно не может рассматриваться как математическая фикция, т.е. делающая легким расчет между частицами взаимодействия. Поле столь же реально, что и частицы.

Рассмотрим теперь область поля имеющий конечный объем и ограниченной поверхностью S. Тогда уравнение (4), выражающее закон сохранения энергии показывает что убыль энергии в единицу времени t,т.е. , равна работе сил поля над зарядами и потоку, вытекающее через замкнутую поверхностьS. Этот поток естественно интерпретировать, как поток энергии электромагнитного поля, вытекающая наружу через поверхность S из объема V.

Поток энергии является потоком энергии электромагнитного поля, так как он отличен от нуля и тогда, когда никакие частицы не пересекают поверхность и не уносят собой энергии.

Поток энергии электромагнитного поля характеризуется вектором (7), которой называют вектором Пойтинга. С учетом обозначений (6) и (7) уравнение (4) можно представить в виде:

(8)

Выражение (8) носит название теоремы Пойтинга.

Закон сохранения энергии в дифференциальной форме имеет вид:

(9)

В теории излучения встречаются поля убывающей с расстоянием по закону при. В этом случаек конечной величине . Физически это обозначает, что система, теряющая часть своей энергии, излучает.

§14. Закон сохранения импульса в электромагнитном поле.

Для системы заряженных частиц и поля рассмотрим изменение импульса частиц, находящихся в объеме V. Можем написать

(1)

Здесь - полный импульс частиц. Из уравнения Максвелла второй пары имеем :и

Следовательно,

Симметризуем в последним уравнении, прибавив в правой части к нулю выражение:

Тогда имеем :

(2)

Рассмотрим интеграл следующего вида:

Равенство:

Вычитая одну формулу из другой получаем формулу:

Далее по теореме градиента: получаем, что

Учитывая симметрию 2-го интеграла формулы (2)отношение векторов иполучаем выражение:

(3)

(4)

- тензор Максвеловских натяжений.

Пусть вектор поля стремится к нулю при быстрее чем, тогда поверхностный интеграл стремится к нулю.

Получаем, что (5)

Суммарный импульс системы состоящий из частицы поля сохраняется. Величина (6) - плотность импульса, т.е. (импульс единицы объема) электромагнитного поля.

Естественно, что (7) - импульс поля в объеме V.

Так согласно (5) имеет место закон сохранения суммарного импульса замкнутой системы. Передача импульса частицам сопровождается потерей импульса поля и наоборот.

В случае конечного объема V закон сохранения дается формулой (3), которую можно переписать в виде:

Пространстве - нормаль к поверхности поток импульса через единичную площадь из объемаV сквозь S, т.е. сила действующая на единичную площадку поверхности.

Легко видеть, что между и вектором Пойтингаимеется связь: