§8. Уравнение Максвелла для поля в веществе. Материальные уравнения.

Уравнение Максвелла для поля в веществе можно получить из уравнений поля в вакууме. Но их надо рассматривать как обобщения законов сохранения.

пара

пара

В этих уравнения появилось два новых вектора инапряжённость магнитного поля и индукция электрического поля. С помощью этих векторов учитывается вклад заряда вещества в общее поле.

В интегральной форме:

пара

пара

Система уравнений (1)-(2) не являются замкнутыми. Это система 8-ми скалярных уравнений относительно 12-ти неизвестных компонент векторов .

Поэтому уравнения Максвелла необходимо дополнить соотношениями, которые связывают векторы и, учитывающие вклад заряда в веществе в общее поле, с векторамии. Уравнения связи можно записать в виде соотношений:(5)

(6)

(7)

Уравнения Максвелла универсальны и пригодны для описания любых сред, в то время как уравнения (5) – (7) существенно зависят от свойства среды, поэтому их называют материальными уравнениями. Эти уравнения могут быть сложными: связь может быть нелинейной, нелокальной во времени и пространстве (т.е. значения ив некоторые моменты времени и в некоторых точках пространства могут зависеть отив других точках и в другие моменты времени). Нелокальность уравнений связи обуславливает такие свойства среды, как пространство и временная дисперсия.

В силу линейности уравнений Максвелла их решение удовлетворяют принципу суперпозиции. Для электромагнитного поля в вакууме, например если - решения уравнений Максвелла, то и,

- тоже решения Максвелла.

Сочетание уравнений Максвелла и линейных уравнений связи составляют основу нелинейной электродинамики.

В простейшем случае матер уравнения имеют вид:

(8)

(9)

(10)

где и- соотв. диэлектрическую проницаемость, магнитная проницаемость и проводимость среды; в общем случаеи- тензоры. Если хотя бы один изи- тензор, то среда анизатропна. В противном случае среда изотропна. Если,зависят (явно) от времени, то среда нестационарна. В противном случае стационарна.

Если ,зависят от координат, то среда неоднородна, иначе - однородна.

Для вакуума:

Истинные физические силовые поля (поля, определяющие силу, которая действует на пробный заряд q) характеризуется векторами и. За векторомсохранилось неудачное название “магнитной индукции”, хотя принято является магнитным аналогом напряжённости электрического поля.

§9. Потенциалы электромагнитного поля.

(1)

-соленоидальный. Его всегда можно положить равным ротору некоторый вспомогательный вектор .

(2)

- вспомогательный вектор, называемый вектор-потенциалом.

Подставим (2) в первое уравнение Максвелла:

Откуда .

Таким образом , является потенциальным и его можно представить в виде:

(3)

- некоторая скалярная функция координат и времени, названная скалярным потенциалом.

нельзя представить в виде градиента от некоторой скалярной функции.

Он имеет вихревой характер:

(4)

причём выражает закон электромагнитной индукции.

Если скалярный и векторный потенциалы введены, то уравнение первой группы Максвелла удовлетворяются тождественно. иопределяются из уравнений второй группы Максвелла.

Учитывая, что , где

получаем: (5)

(6)

Потенциалы А и – вспомогательные величины, введённые для упрощения, они не изменяюти, но позволяют сделать (5) и (6) независимыми. Для однозначного знания полянеобходимо знать его ротор и дивергенцию. Но векторный потенциалА введён посредством (2), т.е. задан лишь ротор , а дивергенция – нет. Зададим её значение:

(7) – соотношение Лоренца.

Тогда (5) – (6) примут вид:

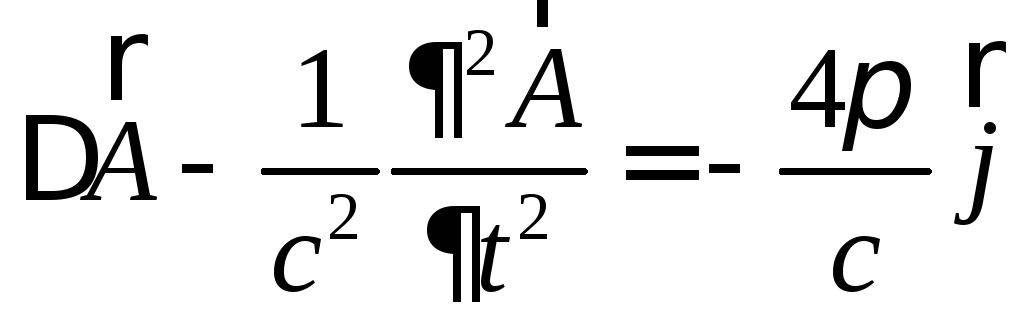(8)

(9)

Т.е. переменные разделились.

(8) – (9) эквивалентны исходным уравнениям Максвелла.

Если заданы , удовлетворяют уравнениям непрерывности, то интегрирование (8),(9) дасти,аиполучим из (2),(4).

Уравнения типа , где- заданная функция координат и времени называют уравнениями Даламбера.

Вводя оператор Даламбера

это уравнение записывают в компактной форме:

(10)

Если ,то (10) переходим в волновое уравнение:

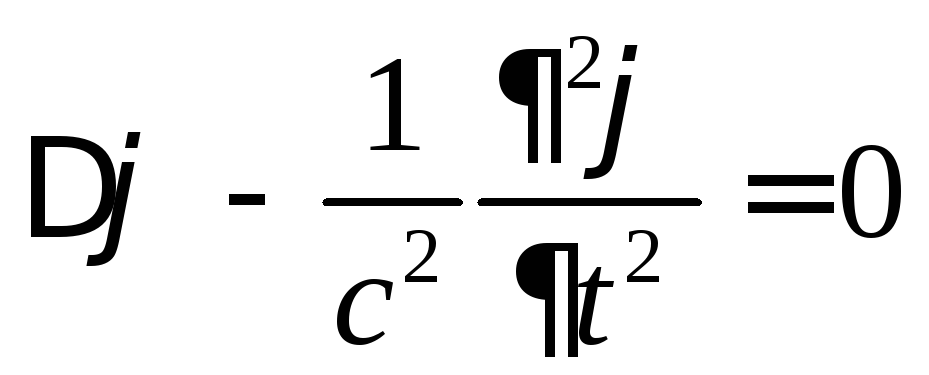(11)

Если ,, (т.е. эти функции не зависят от времени), уравнение Пуассона:

(12)

С математической точки зрения, уравнения (10) – (12) проще уравнений Максвелла (в интегральной форме). Поэтому метод потенциалов представляет основной расчётный аппарат теории поля.