§6. Связь уравнений Максвелла и эмпирических законов электродинамики.

1. Закон Кулона

Окружим точечный заряд сферой радиусаr с центром в точке расположения заряда. В силу изотропности пространства поле заряда должно обладать центральной симметрией Линии напряженности такого поля радиальны а на поверхности сферы напряженность поля постоянна Поэтому четвертое уравнение Максвелла в интегральной форме дает



Учитывая направление вектора (смотри рисунок) получим

 (1)

Если поместить в поле (1) другой точечный заряд , то определению напряженности на него действует сила

 (2)

Это и есть математическое выражение закона Кулона.

2. Закон электромагнитной индукции Фарадея.

Если циркуляцию вектора по замкнутому контору назвать электродвижущей силой индукции,

 (3)

а сам контур заменить проводником, то первое уравнение Максвелла совпадает с законом Фарадея.

 (4)

3. Закон полного тока (закон Ампера).

Пусть переменное электрическое поле отсутствует , тогда для тока, который пересекает поверхностьS, опирающуюся на контур L, получаем:

 (5)

т.е. циркуляция вектора по замкнутому контору (ее называют магнитодвижущей силой) равна сумме токов, охватываемой данным контуром – закон полного тока

§7. Ток смещения.

Формула (5) из предыдущего параграфа выражает закон Эрстеда, установившего в 1820 – 1826 годах связь между электрическим током и магнитными явлениями. Из первого уравнения второй группы следует, что магнитное поле вызывается не только полями, но и переменным электрическим полем тк даже при имеем



или в дифференциальной форме



Имеется двухсторонняя связь между электрическими и магнитными полями переменное электрическое поле порождает магнитное поле а переменное магнитное поле порождает электрическое поле.

Эта закономерность в домаксвелловскую эпоху обнаружена не была поскольку слагаемое обычно очень мало по сравнению с Оба слагаемых могут иметь одинаковый порядок величины при периодическом изменении электрического поля с частотой Гц и выше. А это область радиочастот не доступная физике 19-го века

Правильно истолковав явление электромагнитной индукции возникает электрическое поле при изменении магнитного, Максвелл предположил, что существует и обратный процесс : возникает магнитное поле при изменении электрического. Уравнение  не удовлетворяющее закону сохранения заряда было дополнено слагаемым , так что получившееся уравнение

(2)

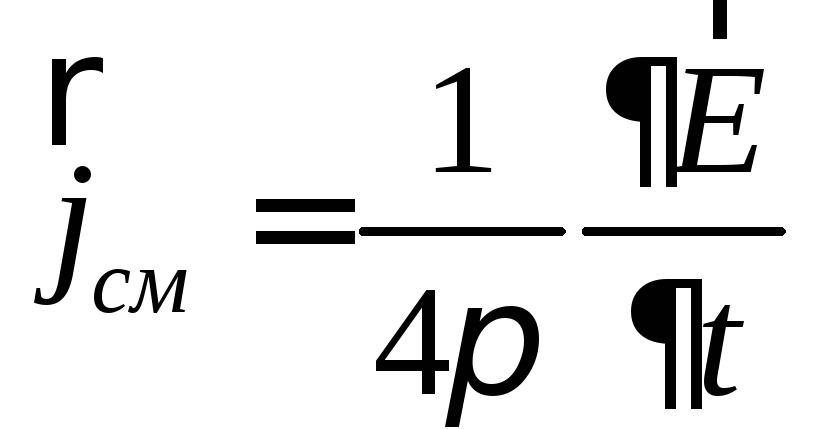(3)

удовлетворяло закону сохранения заряда. Величина была названа Максвеллом током смещения

Схема рассуждений  приводящих к обобщению (2) может быть такой Запишем (2) в следующем виде:

 (4)

где – неизвестный вектор.

Возьмём дивергенцию от обеих частей:



те

 (5)

Вектор дополняеттаким образом, чтобы суммарная величинаобладала свойствами соленоидального вектора Из (5) требуя выполнения закона сохранения заряда и используя четвёртое уравнение Максвелла получим

откуда следует что

,

где – произвольный соленоидальный вектор.

Вообще говоря, нет оснований заранее считать , однако для получения симметрии между электрическими и магнитными полями полагают что и приводит к знаменитому уравнению

.