§62. Плоские волны в магнитоактивной плазме.

Решив уравнение для в-ри имеет вид:

а дисперсионное уравнение, т.е. условие существования нетривиального решения .

Из находим показатели преломления обыкновенной и необыкновенной волн.

подставляя впосле простых преобразований получаем:

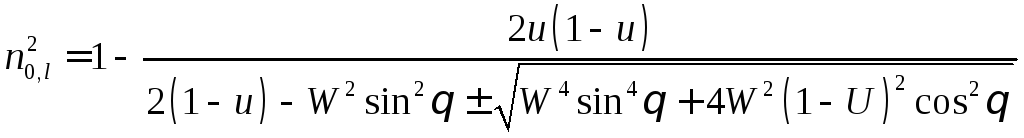
Т.к. ифункции частоты, тоопределяет закон дисперсии показателей преломления в магнитоактивной плазме.

Состояние поляризации обыкновенной и необыкновенной волн можно определить.

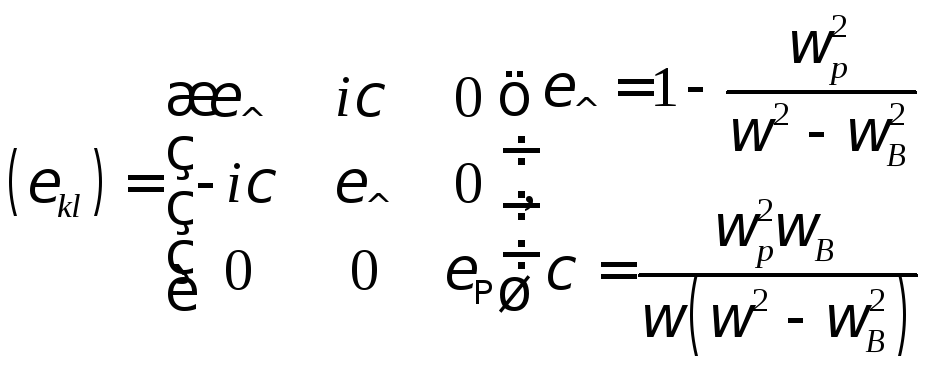
И тогда какая-то хрень

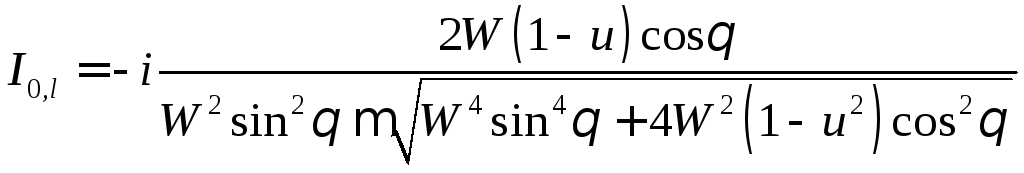
Это означает, что поляризация обыкновенной и необыкновенной волн эллиптическая, причём направление вращения плоскости фронта

Направление обхода в обыкновенных и необыкновенных волнах противоположное. Легко проверить, что

оси эллипсов поляризации обыкновенных и необыкновенных волн взаимно перпендикулярны.

Если (т.е. гиромагнитной частоты) и соответственно

, то влияние электрического поля слабое.

- Две волны с круговой поляризацией и противоположным вращением вектора .

Если волна распространяется вдоль , тогда

Поляризация круговая

Направление вращения вектора для необыкновенных волн такое же как направление вращения электронов в магнитном поле. Это приводит к резонансу поглощения необыкновенных волн при.

Для обыкновенной волны детерминант волнового уравнения . Т.е.направлено вдоль поэтому показатель преломления её совпадает с показателем преломления изотропной плазмы. Для необыкновенной волны детерминант , а отношениет.е. волна поляризована эллиптически в плоскости.

§63. Тензор диэлектрической проницаемости ферритов.

Феррит – это ферромагнитные полупроводники и диэлектрики

.

- двух валентный металл.

Можно считать, что при магнитная проницаемость феррита скалярная величина, а анизотропная как и в плазме создаётся постоянным или медленно меняющимся полем. Данное представление является приближённым, т.к. реальные ферриты обладают кристаллографической анизотропией, т.е. зависимостью магнитных свойств от направления намагничивания относительно осей кристаллографической решетки.

Т.к. учёт этой анизотропии не меняет вид , а лишь меняет его компоненты. Будем считать это изотропная среда.

Известно, что молекулу феррита, обладающие магнитным моментом, обладают спиновым эффектом. Анизотропия возникает из-за прецессии магнитный диполей вокруг спиновых линий магнитного поля. Запишем излучение по закону Ландау-Лившица:

- постоянная поля и постоянная намагничивания, совпадает с .

- гармоническое соотношение для элементов ,, тогда

Или обозначить

, , топерепишем в виде

Если разложить по проекторам

получим

В декартовой системе координат си осьювдоль, тензоримеет вид:

Тензор феррита имеет такой же вид, что и тензор диэлектрической проницаемости плазмы в магнитном поле, он Эрмитов в то время как- скаляр.

Феррит – это магнитоактивная среда; а нормальные или собственные волны должны иметь круговую или эллиптическую поляризацию.

113