§ 60 Резонаторы

Вдоль оси волновода возникает бегущая волна в одном направлении. Из-за отражения симметричной волны, возникают стоячие волны. Перегородим волновод плоскостями и. Из-за отражения от этих торцевых поверхно­стей и вдольвозникает бегущая стоячая волна. Принципы установления на торцах те же, что и на боковых поверхностях, т.е. равны нолю поперечная составляющая вектораи нормальная составляющая вектора. На примере прямоугольного волновода мы видим, что продольные компоненты полей в волноводе имеют вид:

где произвольная комплексная амплитуда.зависит от типа волны (ТМ и ТЕ, ТЕМ-волна), поэтому поле бегущей волны в положительном направлениипропорционально, а поле бегущее в отрицательном направлении пропорционально.

Для -волны (ТЕ) граничные условия:

даст, что

В случае -волны (ТМ) условия обращения в нольна торцах волновода приводит к требованию

нормальный контур производной от

, тогда

Т.о. в перегороженном волноводе величина становится вместо непрерывной дискретной.

Поскольку , то

, где

критическая частотаколебаний

- т.е. эта величина определяется тремя числамии, ее логично обозначать

Периодический волновод имеет дискретный спектр частот. Вообще любая полость полностью изолированная от окружающего пространства обладает дискретным спектром частот, зависящих от геометрии полости, причем каждая частота определяется тремя числами. Такую полость называют резонатором, а собственные частоты – частотами резонатора. Резонаторы широко используются в качестве СВЧ.

Если бы стенки полости характеризовались проводимостью (представим излучательный проводник), то поле бы в них не проникало и ЭМ энергия в резонаторе бы сохранялась. В действительности ЭМП проникает вглубь стенок резонатора и превращается в тепло, поэтому ЭМ энергия, запасенная в резонаторе постепенно уменьшается. Отношение энергии, запасенной в резонаторе и энергии теряемой за период колебаний обозначаетсяи называется добротностью резонатора.

Пусть - энергия резонатора в момент времени, то, т.е., гдерезонансная частота.

Т.о. поле в резонаторе изменяется не по закону , а по закону. Она может быть представлена в виде, где.

Энергия в интервале очевидно пропорциональна. Легко убедится, что. Интенсивность поля, как функция частоты имеет следующий вид:

Ромич не забудь нарисовать график!!!

Интенсивность поля вдвое меньше максимальной, если частота пропорционально отношению резонансной частоты к ширине резонансной кривой.

можно определить формулой:

,

где глубина смещения сигнала,объем резонатора,безразмерный фактор, зависит от геометрии резонатора и структуры резонансного поля.

§ 61. Магнитоактивные среды. Тензор диэлектрической проницаемости плазмы в постоянном магнитном поле.

.

Тензоры и в таких средах несимметричны.

. (1)

Действительная и мнимая части должны быть соответственно симметричными и антисимметричными тензорами:

, . (2)

Если тензором является , а — скаляр, то среда называется гироэлектрической.

Рассмотрим магнитоактивную плазму. Чтобы найти явный вид , рассмотрим движение электронов, ионов и нейтральных молекул плазмы в присутствие постоянного магнитного поля и переменных волновых полей.

В общем случае система кинетических уравнений для электронов, ионов и нейтральных молекул очень сложна и мы рассмотрим лишь приближенное решение динамической задачи.

Если частота волны

, (3)

где —частота вращения ионов в магнитном поле , —масса ионов, е—заряд ионов, то при определении поляризации среды можно считать ионы неподвижными и учитывать только движение электронов.

Волны, для которых выполняется (3)—высокочастотные.

Если

, (4)

где — частота соударений электронов с молекулами или ионами, то токи смещения в среде должны преобладать над токами проводимости. При этом в поле электромагнитной волны происходит пространственное распределение зарядов, что приводит к возникновению сильных электрических полей, стремящихся сблизить заряды. В результате возникают колебания в плотности зарядов с частотой

,

где N — плотность электронов, m — масса электрона.

Пусть (3) и (4) выполнены. Когда поля высокочастотные и токами проводимости можно пренебречь по сравнению с токами смещения, не целесообразно рассматривать ток в среде как их сумму. Вместо этого вводят полный ток , где —полный вектор поляризации среды.

Считаем, что все величины изменяются по гармоническому закону, то есть .

Считая, что полный ток равен току смещения, получаем, что

. (5)

Учитывая, что , из (5) получаем, что

, (6)

где , . (7)

Для каждого электрона запишем

. (8)

Учитывая (8), (7) можно представить в виде

, (9)

где ; — гиромагнитная частота

Из (9) получаем

, (9’)

, (10)

.

Если , то есть , то из (9’) получаем, что

. (11)

С учетом (11) из (6) находим (поскольку )

. (12)

Далее выделим действительную и мнимую части у :

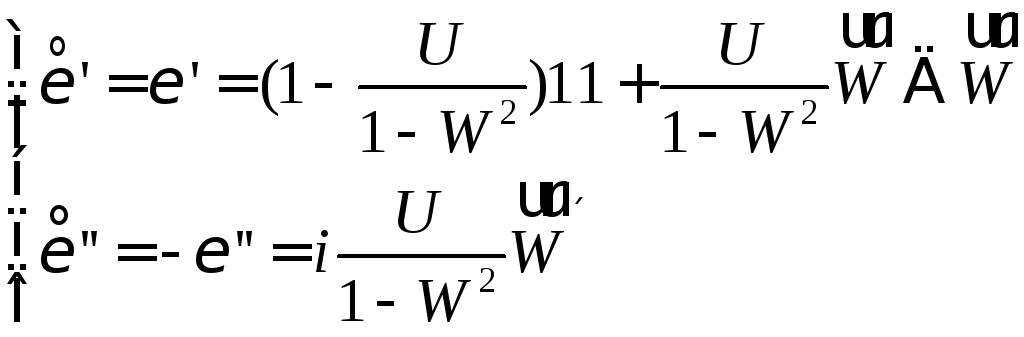
Обозначим через .

Обозначим далее

.

Очевидно, что в направлении вектора векторы и параллельны.

.

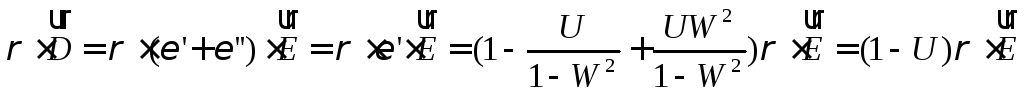В плоскости, перпендикулярной , для векторов и имеем

, ,

,

.

Таким образом, не параллелен .

Но если , то есть волна имеет круговую поляризацию и

,

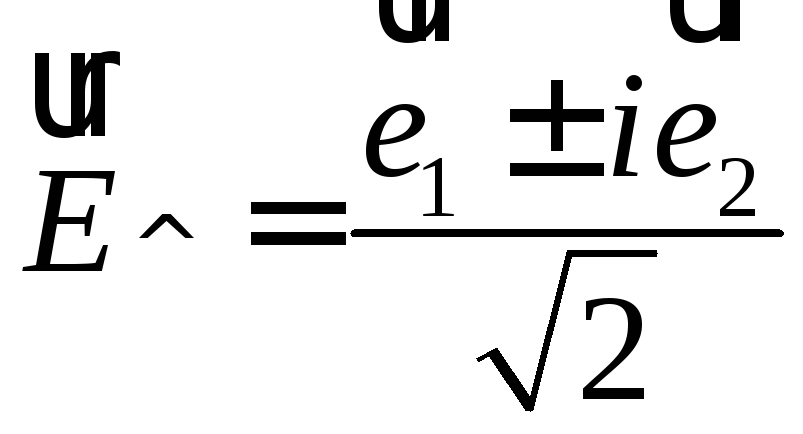где ,,.

.

Получаем, что в случае круговой поляризации .

В магнитоактивной среде собственные или нормальные волны в плоскости, перпендикулярной , имеют либо круговую поляризацию, либо, в общем случае, эллиптическую.

Из (11)-(13) видно, что при некоторые компоненты обращаются в бесконечность, что свидетельствует о существовании резонансных явлений при .

Эти формулы получены без учета потерь энергии, теряемой при соударениях увлекаемых волной электронов с ионами и нейтральными молекулами.

С учетом соударений резонансные явления проявляются в резком увеличении поглощения необыкновенной волны, направление вращения в которой совпадает с направлением вращения электронов во внешнем поле .