§501. Рассеяние света на свободных зарядах. Формула Томсона.

Пусть свободный заряд находится в поле плоской монохроматической волны . Под действием поля заряд придет в неравномерное прямолинейное движениебудет излучать вторичные волнырассеивание первичной волны.

Поток энергии через векторную площадку , стягивающую телесный угол, т.е.

.

Если волна имеет плотность потока энергии

,

а поток энергии вторичной волной в направлении в телесный угол:

,

где , то величину- дифференциальное эффективное сечение рассеяния,- вектор пойтинга волны.

Реально измеряются лишь энергетические величины усреднённые по промежуткам времени чем период. Поэтому эффективное дифференциальное сечение определяет отношение таких средних

, где - усреднение по времени

т.к. ,.

В рассеянной волне будем учитывать лишь электрическую дипольную часть

Установим связь между ,

Учитывая, что в дипольном приближении

Соответственно:

,, откуда

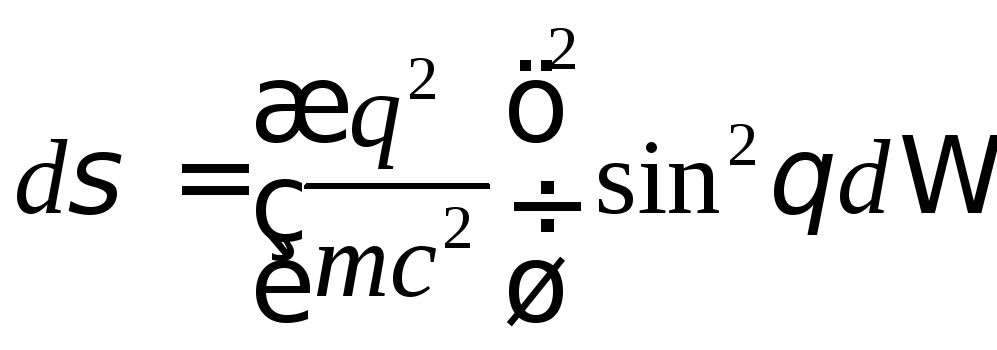
,- классический радиус электрона.

Здесь - угол между направлением рассеянияи направлением поляризации.

Пусть волна распространяется вдоль оси . Рассеяние происходит вдоль плоскости

- направление рассеяния волны.

Направление поляризации, лежащее в плоскости отклонено отна. Если обозначить черезугол рассеяния, то

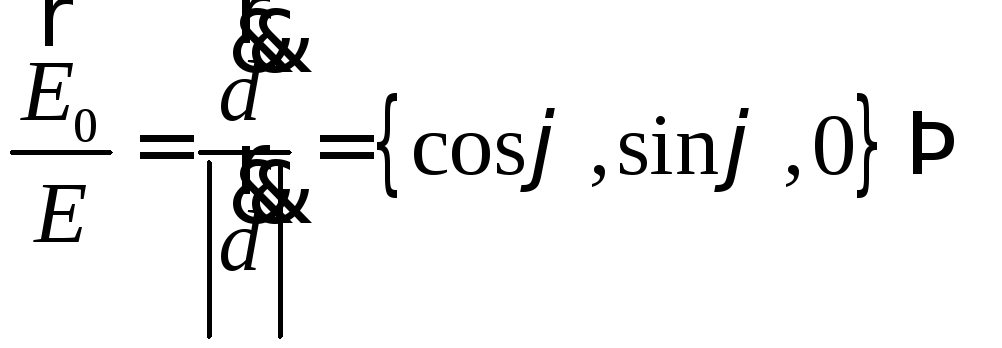
Эффективное дифференциальное рассеяние.

задаёт ориентация поляризации плоско-поляризованной волны.

Свет от естественных источников редко обладает определённой поляризацией. Он обладает плоскополяризованной волной, направленной по разному не когерентных между собой. Складываются энергии, а не поля усреднитьпо всем.

Поэтому для неполяризованной волны:

Полное эффктивное сечение рассеяния на свободном заряде получается интегрированием по углам и приводит к формуле Томсона:

§502. Рассеяние света на свободных зарядах. Формула Томсона.

Пусть заряженная частица массой и зарядомнаходится в поле плоской электромагнитной волны,. Под действием поля заряд придет в неравномерное прямолинейное движение и, следовательно, будет излучать вторичные электромагнитные волны, т.е. будет происходить рассеивание первоначальной волны. Поток энергии через элементарную площадку, стягивающей телесный уголназывается интенсивностью излучения:

Если падающая волна имеет плотность потока энергии , а поток энергии уносимый вторичной волной в направлениив телесный уголесть, то величинуестественно называют дифференциальным эффективным сечением рассеивания. Т.к. приборы для обнаружения электромагнитных волн обладают инерционностью колебаний больше чем период, то реально измеряются лишь физические величины усредненные по промежутку времени. Поэтому величину эффективного дифференциального сечения определяют именно как отношение таких средних:

(1)

Т.к. ,

В рассеянной волне будем учитывать лишь Эл. Дипольную часть. Тогда:

(2)

Установим связь между вектором и. Для этого из уравнения движения заряда:

учитывая, что в дипольном приближении ,,находим:

Для одного заряда ,откуда эффективное дифференциальное сечение рассеивания:

(3)

Если речь идет об электроне, то , где-классический радиус электрона.

Угол - это угол между направлением рассеиванияи направлением поляризации,

Но не направлением её распространения . Пусть волна распространяется вдоль оси, а рассеивание происходит в плоскости, а направление поляризации, лежащее в плоскости, отклонено от осина угол.

Если обозначить угол рассеивания через , то :

Следовательно:

(4)

Замечание: угол задает ориентацию плоскости поляризации плоскополяризованной волны. Свет от естественных источников редко обладает определенной поляризацией. Обычно он представляет собой смесь плоскополяризованных волн со всевозможными направлениями поляризаций, некогерентных между собой. При вычислениипоэтому складываются энергии, а не поля, так что следует усреднить (4) по всем:

Поэтому для неполяризованной волны:

Полное эффективное сечение рассеивания света на свободном заряде получается интегрированием по всем углам и приводит к формуле Томсона: