§3. Дипольное излучение простейших систем.

В случае одиночного заряда, получающего ускорение под действием силы , дипольный момент:

Поэтому , т.е. имеем уже известную формулу Лармора. Рассмотрим систему, состоящую из двух зарядовиcмассамии, и для нее получим, что:

Если система замкнута, то , а, где- сила с которой вторая частица действует на первую. Поэтому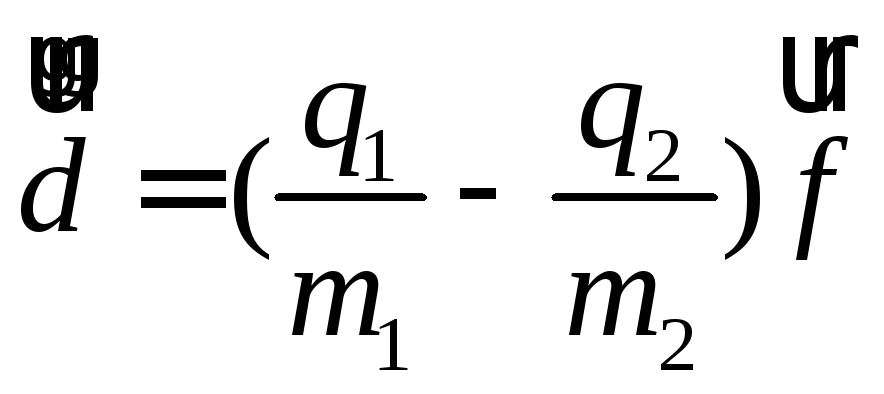или:

Таким образом система, состоящая из одинаковых частиц или частиц с одинаковым отношениемq/mне может излучать в дипольном приближении.

§4. Квадрупольное и магнитное дипольное излучение.

Если в дипольном приближении излучение отсутствует, то следует учитывать старшие члены разложения по степеням собственного запаздывания в системе, которую будут определять излучения высших порядков: квадрупольное, октупольное.

Рассмотрим приближение следующего после дипольного порядка. Запишем вектор-потенциал в виде:

(1)

описывает дипольное приближение. Рассмотрим :

(2)

Здесь воспользовались тем, что ине зависят от времени. Далее по формуле

преобразуем (2) к виду:

(2’)

Первый интеграл можно представить в виде:

(3)

где -- магнитный момент системы зарядов.

Например, для любой трубки с током , где:

- сечение;

- постоянный ток;

- элемент длины трубки;

Тогда, . Видно, что величина- это площадь боковой поверхности конуса, опирающегося на контур с током. В частном случае плоского замкнутого контура заможно выбрать вектор нормали к поверхности контура, умноженный на его площадь. Тогда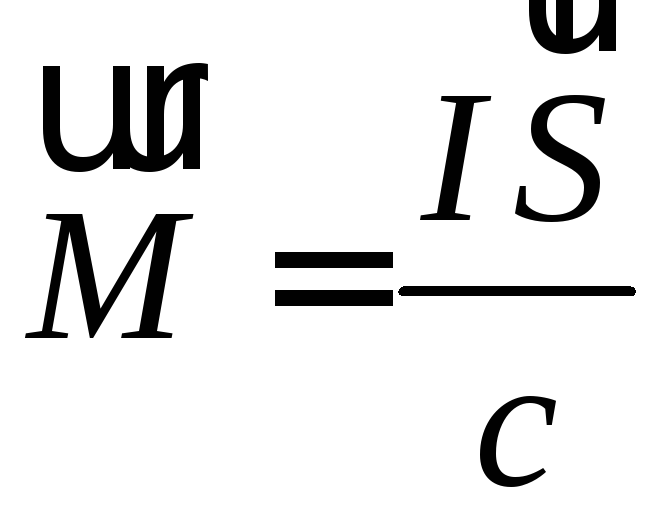-- формула имеет наглядную интерпретацию: всякий замкнутый ток (например одна или несколько частиц движется по замкнутой траектории) обладает магнитным моментом пропорциональным величине тока.

Второй интеграл представим виде:

Для системы точечных зарядов:

-- тензор квадрупольного момента системы зарядов. В случае непрерывного распределения зарядов имеем:

Для имеем:

(5)

Первое слагаемое описывает дипольное излучение; второе – зависит от производной по времени от магнитного момента системы и соответствующее ему слагаемое называется магнитным дипольным излучением; третье—определяет квадрупольное излучение. Оценим порядок величин в (5):

поэтому:

Величина

-- характерный размер системы.

Т.к. в данном приближении и, то слагаемое, отвечающее магнитному дипольному приближению и квудрупольному приближению весьма малы по сравнению с первым, отвечающим дипольному излучению. Таким образом они играют роль только для систем, у которых дипольное излучение отсутствует.

Пример, квудруполь: электронейтральная система с нулевым дипольным моментом-- это 2 равных по величине диполя с противоположными по направлению дипольными моментами и находящиеся бесконечно близко друг к другу.

Магнитное дипольное излучение отсутствует у систем, магнитный момент которых сравним с механическим моментом. Например для системы из двух произвольных частиц, у которых отношение q/mодинаково. Поэтому это излучение отсутствует при соударениях двух частиц.

Тензор Qопределяется неоднозначно. Его можно так изменить, что это изменение не приведет к изменению потенциалов. Обычно вместоQрассматривают тензор, обладающий важным свойством: его след равен 0.