§12. Движение заряженных частиц в линейных и циклических условиях.

Полученные в предыдущем параграфе формулу для мощности использовали при расчете ускорителей заряженных частиц. В ряде случаев потери на излучение является главным фактором, ограничив практически достижимую энергию в ускорителе. При заданной внешней силе, т.е скорости изменения импульса (обратно пропорциональна квадрату массы ускоряемой частицы), следовательно влияние этих радиационных эффектов максимально для электронов. Поэтому именно излучение электронов.

(1)

Конкретно, рассмотрим два случая:

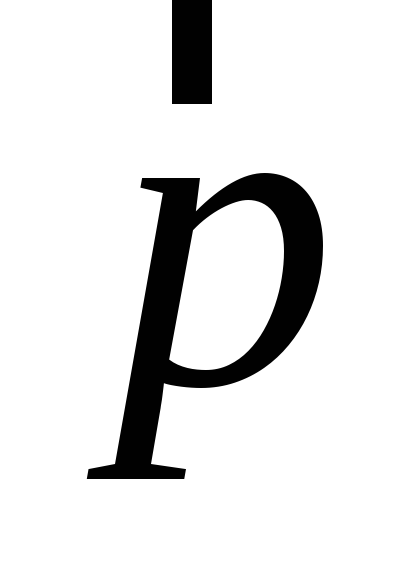1. не меняет направления (например, в линейных укорителях).

Тогда 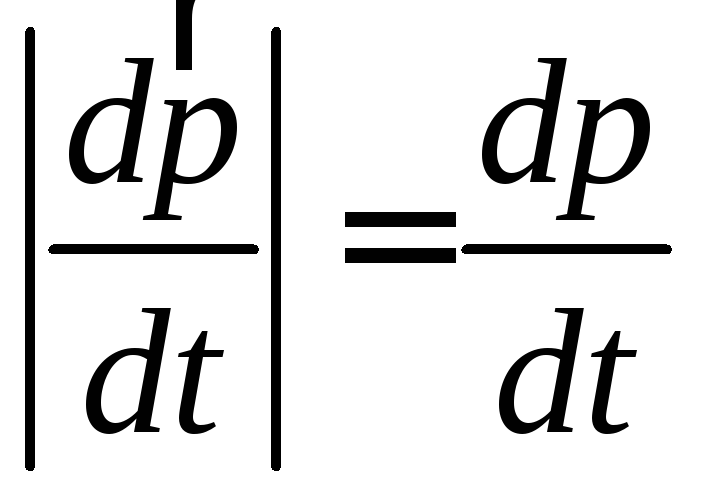, следовательно(2)

Пусть движение происходит вдоль оси x, тогда

В дальнейшем будем писать , предполагая что E=E(x).

Вычислим отношение мощности, уходящей за счет излучения к подводимой мощности.

Получим

Рассмотрим релятивистский случай

для электрона, например , МэВ

Обычно измерения, т.е. энергии в линейных ускорителях .

Чтобы эффективно ускорять частицы, надо, чтобы потери мощности за счет излучения были малы по сравнению с подводимой мощностью. Для этого надо чтобы прирост энергии dE на расстояние было много меньше чем . В нашем случае . Из приведенных оценок ясно, что в линейных укорителях потери на излучение пренебрежительно малы.

2. , но направление быстро меняется (например, циклические ускорители,

типа синхротрона или бетатрона) излучение частиц в такого рода ускорителях называют синхротронными.

В таких ускорителях используются электромагнитные поля высокой частоты (СВЧ). Энергия частицы за один оборот изменяется мало, а направление - сильно.

Поэтому имеем

(3)

Пусть частица движется равномерно по круговой орбите радиуса R с частотой , которой задается вектором.

Вводя оператор поворота на угол вокруг:

где в нашем случае , получаем, что

Пусть , тогда

Следовательно:

(4)

Так как, , следовательно,

(5)

Основная формула для расчета мощности излучения в циклическом ускорителе.

За один период на излучение теряется энергия

(6)

Для больших электронных синхротронов максимальная энергия.

При этом потери на излучение за один оборот.

Практически очень трудно получить высококачественную мощность, обеспечивающую на много больший прирост мощности на обороте, так что энергия 5-10 ГэВ представляет верхний предел достижимых энергий в циклических электронных ускорителях.

Глава 3. Глава Поля ограниченного распределения зарядов (поля островных сил).

§1. Потенциал электромагнитного поля вдали от излучателей в дипольном приближении.

Ещё более упростить формулы для потенциалов можно, используя для приближение:

( )

При этом полное время запаздывания слагается из двух частей: Первая,, называемая временем запаздывания системы, представляет время распространения электромагнитного поля от начала координат до точки наблюдения. Вторая,, называемая собственным запаздыванием – это время, требующееся для распространения поля, в пределах системы. По порядку величины ,так что при собственное запаздывание.

В принципе, плотность заряда можно разложить по малому параметру :

( )

При этом, однако, не должна являться быстро изменяющийся функцией своего аргумента, т.е. за время конфигурация зарядов в системе не должно успеть сильно измениться. За время заряды проходят путь .Если этот путь мал по сравнению с размерами системы, то есть

или ( )

то разложение ( ) правомерно.

Подставляя тогда ( ) в ( ) и ограничившись членами разложения с наименьшими степенями получим

где .Слагаемоемало по сравнению с на достаточно большом удалении от системы.

Т.к. в формуле все величины берутся в один и тот же момент времени, то - это просто полный заряд системы в момент времени . Для электронейтральной системы он равен нулю. В этом случае

( )

Воспользовавшись уравнением непрерывности перепишем интеграл в правой части

Последний интеграл удобно вычислить в координатном представлении

где и– границы области движения зарядов, на которой плотность тока обращается в ноль.

В векторном виде будем иметь

( )

Подставляя ( ) в ( ) находим

( )

Аналогично, для потенциала получаем

( )

Так что

( )

Введем понятие дипольного момента системы зарядов:

( )

Например, для системы состоящей из двух равных по величине и противоположных по знаку зарядов, , именуемой диполем

Теперь, используя определение ( ), мы видим, что

Здесь мы учили, что - переменная интегрирования, независимая от. Следовательно

( )

( )

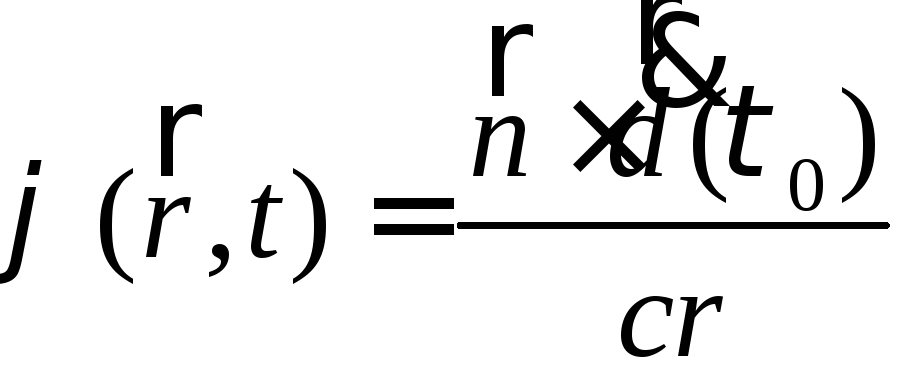Итак, в рассматриваемом приближении потенциалы поля вдали от системы определяются значением производной по времени от её дипольного момента. Поэтому такое приближение называется дипольным. Оно применимо при выполнении условия ( ).

Легко проверить, что в этом приближении потенциалы удовлетворяет калибровке Лоренца

Смысл полученных результатов прост: при движении зарядов в системе (изменений её дипольного момента) в окружающим пространстве возникает электромагнитном поле.

Потенциалы этого поля убывает по закону , в то время как потенциалы электростатического поля по закону.

Система неравномерного движущихся зарядов является излучателем.