§10. Потенциалы Ликнара – Вихерта и поле точечного заряда.

Пусть имеется точечный заряд движущийся со скоростью,отвечает точке наблюдения,интегрируем.

Формулы (20) - (21) для запаздывающих потенциалов можно объединить в одну для 4- потенциала . Тогда можно написать

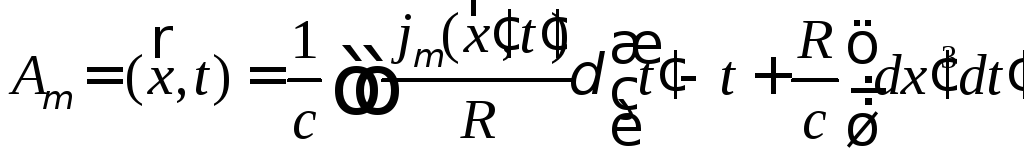(1)

где , а- функция обеспечивает запаздывание потенциалов. Так как рассматривается движение точечного зарядаq, то для

(2)

где (3)

Интегрирование по объёму проводится сразу

где теперь .Для интегрирования повоспользуемся известным соотношением

(5)

В нашем случае т.е.

Следовательно

т.е. (6),

Интегрирование с использованием дает потенциалы произвольным образом движущегося заряда – потенциалы Ликнара – Вихерта:

(7)

где индекс запаздывающий означает, что величины в (7) следует брать в момент времени , определяемый из соотношения

(8)

Для нерелятивистского движения .

Используя определение идля векторовиможно найти

(9)

Первое слагаемое зависит лишь от и фактически имеет статический характер, убывая с расстоянием, как.

Вторая линейно зависит от и является типичным поперечным полем излучения, для которогои изменяется как.

§11. Полная мощность, излучаемая ускоренно движущихся зарядом. Формулы Лармона и Лиенара.

Если ускоренно движется заряд наблюдать из ИСО, в которой , то второе слагаемое, дающее вклад в излучение в (9) примет вид:

(1)

Мгновенный поток энергии определяется вектором Пойтинга:

(- вещественный вектор).

Вспоминая определение телесного угла:

,

Находим, что мощность излучаемая в телесный угол равна

Следовательно

(2)

Используя формулу

Находим

(3)

Видно, что наибольшая мощность излучает движущий заряд отвечает

Из формулы (1) следует, что вектор лежит в плоскости векторови(излучение поляризована в плоскости,).

Интегрируя (3) по всем телесным углам, находим полную мгновенную мощность излучения.

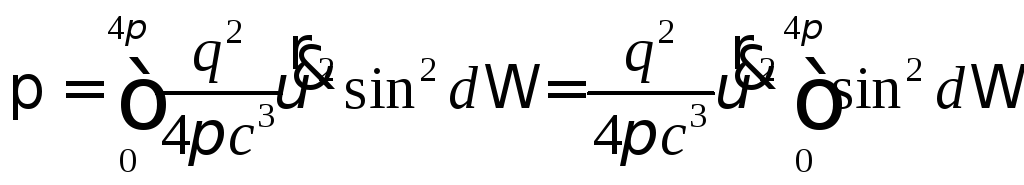
так как, , то, таким образом

(4)

Это известная нерелятивистская формула Лармора для ускоренно движущегося заряда.

Обобщим её на случай произвольно движущегося заряда. Так как. Энергия электромагнитного излучения при преобразованиях Лоренца ведет себя как четвертая (временная) компонента 4-вектора, то - инвариант преобразований Лоренца.

Если удастся найти инвариантное относительно преобразований Лоренца выражение, переходящее в (4) при , то это и будет требуемое обобщение. Конечно существует много величин, сводящих прик (4), но искомое выражение должно зависеть лишь оти. При таком ограничении, накладываемой на порядок производных, результат оказывается единственным.

Перепишем (4) в виде:

где m - масса заряженной частицы, - импульс.

Лоренц – инвариант обобщенного этого соотношения очевидно

(5)

где - собственное время , а- 4-вектор энергии импульса .

Очевидно, что отсюда следует

(6)

Так как ,(7) , то

, следовательно

(8)

Из последней формулы при действительно получаем формулу Лармора.

Выражая с помощью (7) все величины через скорость и ускорение, находим

,

,

(*) -

Формула Лиенара.