§9. Запаздывающие потенциалы.

Пусть в некотором объеме совершает движение системы зарядов, распределение и движение, которых характеризуется заданными функциями икоординат и времени.

В случае калибровки Лоренца:

(1)

Уравнения для потенциалов электромагнитного поля иимеют вид:

(2)

(3)

Для однозначного решения системы уравнений (1) – (3) известных функций необходимо задать начальные и граничные условия для A и φ.

Обычно задача формулируется так: до некоторого начального момента времени t=0 (t<0) заряды неподвижны, а начиная с момента времени t=0 при t>0 приходят в движение. При этом в электромагнитном поле возникает изменение (возбуждение). Будем полагать, что в (1) – (3) фигурируют потенциалы именно возмущенного поля. Функции ,ответственные за возмущение поля приt>0 считается известными. При следует положить:

, .

Соответственно, ,. Тогда начальные условия для потенциалов таков:

, ,(4)

Из определения ивидно, что при этом векторы поля действительно равны нулю.

В качестве граничных условий выбирают обычно условия

, при,(5)

Т.е. идолжны убывать на медленнее функциипри.

Для решения системы (1) – (3) воспользуемся простым хотя и не строгим методом, основанном на принципе суперпозиции.

Разобьем систему на совокупность сколь угодно малых зарядов , где- сколь угодно малый объём в. Найдём потенциалы поля, создаваемые зарядомв точке наблюдения, считается что никаких других зарядов в пространстве нет. Полное же поле найдем суммируя поля, создаваемое всеми зарядамисистемы. Кажущееся нарушения закона сохранения заряда – не существуют уединенные переменные во времени заряда – не отразится на конечном решении, в котором будет проведено суммирование ко всем зарядам систем.

Найдем сначала потенциалы поля, создаваемые зарядами вне объема. Уравнения (1) – (3) примут вид:

(6)

Введем сферические координаты с началом в объеме . Поле вне объемаимеет сферическую симметрию и зависит только от расстояния до точки наблюденияr. В сферических координатах (6) имеют вид

(7)

Т.е. определяются уравнением одного вида

(8)

которое называют волновым уравнением.

Будем решать его методом Даламбера.

Перепишем (8) в виде:

или

(9)

где (10)

Перейдем в (9) к новым переменным

(11)

Откуда

, (12)

так, что

Следовательно

(13)

Итак, в новых переменных уравнение (9) имеет вид

(14)

и интегрируется непосредственно. Оно удовлетворяется любыми функциями иодной переменойлибо. Поэтому общее решение можно записать в следующем виде

или, возвращаясь к старым переменным,

(15)

Это решение имеет простой смысл. Значение в точкев момент временисовпадает со значениемв точке r в момент времени t. Таким образом описывает периодический во времени и пространстве процесс – волновой процесс. При этом волна распространяется в сторону возрастающих значенийr со скоростью c. Аналогично описывает волну идущую от большихr к меньшим. Для функции имеем

(16)

Следовательно, общее решение уравнения (8) описывает наложения двух волн - сходящихся и расходящихся. Поверхности сфер являются поверхностями постоянного значенияили поверхностями равной фазы. Поэтому говорят, чтоописывает волновой процесс, который является совокупностью сходящейся и расходящейся сферических волн.

Любые из величин можно представить в виде (16). Рассмотрим одно из частных решений, например, сходящуюся волну. Для скалярного потенциала будем иметь

(17)

Вне объёма (17) справедливо любое.Потребуем чтобы (17) непрерывно переходило в решение исходного уравнения (2) вблизи объёма(вблизи точки расположения заряда).

Если в (2) совершить формальный переход , то оно превратиться в уравнение для электростатического потенциала, решением для которого служит

(18)

Поэтому, записав (17) в виде

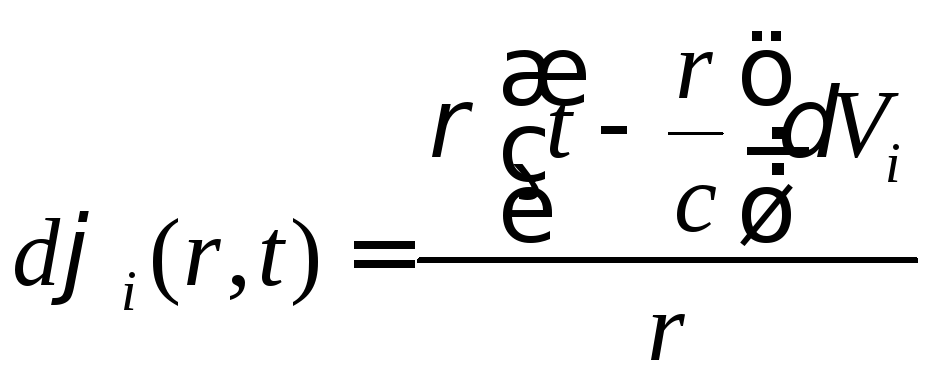(19)

мы получим выражение для потенциала поля, создаваемого зарядом , которое удовлетворяет уравнению (7) и переходит вблизи начала координат в (18).

Формула (19) показывает, что потенциальное поле в точке, находящееся в момент времени t на расстоянии r от начала координат, определяется значением заряда в предшествующий момент времени . Поэтому потенциал (19) называют запаздывающим потенциалом, а величину- временем запаздывания. Это время, за которое распространяющееся со скоростьюс электрическое поле проходит путь r.

Вводя начало координат в некоторой точке О, расположенную в объёме и синтезируя по всем зарядам системы получим следующее выражение для потенциала поля в точке наблюдения

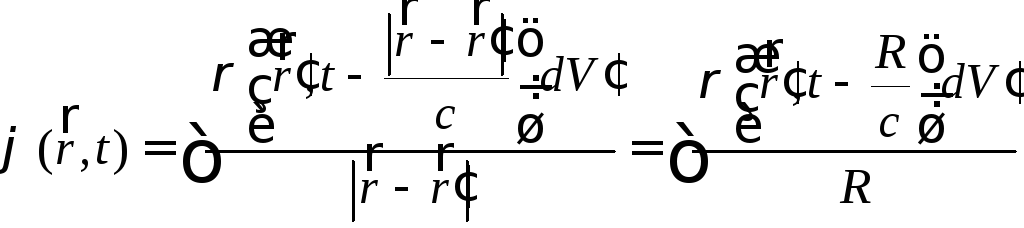(20)

где - переменная интегрирования( место положительного элементарного объёма), а.

Аналогично, для вектор-потенциала

(21)

Наряду с этими решениями в виде запаздывающих потенциалов можно записать аналогичные в виде опережающих потенциалов.